Решение

Р абота, совершаемая силами электростатического поля по перемещению заряда из точки 1 в точку 2, может быть выражена по формуле А = q(₁ - ₂), где ₁ и ₂ – потенциалы электрического поля, созданного полукольцом в центре и на бесконечности. Примем ₂=0. Тогда

А = q₁. (1)

Потенциал ₁ найдём, используя принцип суперпозиции для потенциала поля, созданного непрерывно распределёнными зарядами. Для этого разобьем полукольцо на элементарные отрезки длиной dl. Заряд, находящийся на каждом из них, можно считать точечным: dq = dl. Потенциал поля такого заряда в точке 1

.

Интегрируя полученное выражение в пределах от нуля до длины полуокружности l = R, получим искомый потенциал:

₁= , . (2)

Подставим уравнение (2) в уравнение (1) и получим

А = q₁ = .

Подставим числовые значения заданных величин:

Дж.

4. Металлическому шару радиусом R сообщили заряд Q, после этого поверхность шара покрыли слоем диэлектрика толщиной h. Чему равна плотность связанных зарядов на внешней и внутренней поверхностях диэлектрика и полный наведённый заряд, если относительная диэлектрическая проницаемость диэлектрика .

Решение

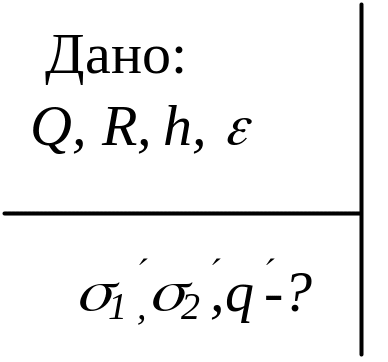Применим теорему Гаусса для вектора . Поверхность интегрирования выберем в виде сферы с радиусом равным r и центром, совпадающим с центром металлического шара:

.

Ввиду симметрии задачи интеграл в левой части

.

Сравнивая две формулы, получим выражение для модуля электрического смещения:

D = Q/4r ².

С другой стороны, по определению

.

Используя связь между вектором поляризации и напряженностью электрического поля, запишем

, ,

где  – восприимчивость диэлектрика.

Подставим это выражение в формулу для электрического смещения

.

Учитывая, что векторы и параллельны, и используя результат применения теоремы Гаусса, запишем выражение для модуля вектора поляризации

.

Вектор перпендикулярен поверхности диэлектрика и нормальная составляющая вектора поляризации равна поверхностной плотности связанных зарядов:

P = P _n =  ^.

Тогда плотность связанных зарядов на внутренней поверхности диэлектрика рассчитывается при r=(R+0)

,

и полный заряд, наведенный на внутренней поверхности диэлектрика и связанный с ₁^ соотношением q ^ = 4R²₁^

.

В силу закона сохранения заряда точно такой же по модулю, но противоположный по знаку заряд должен появиться на внешней поверхности диэлектрика. Очевидно, что его плотность

.

5. На два последовательно соединенных конденсатора С₁ = 100 пФ и С₂ = 200 пФ подано постоянное напряжение U = 300 В. Определить энергию, запасенную в каждом конденсаторе.

Решение

Так как обкладки конденсаторов соединены, то заряд, появляющийся под действием приложенного напряжения на первом конденсаторе, равен заряду, появляющемуся на втором конденсаторе (явление электростатической индукции). Поскольку заряд связан с емкостью конденсатора и напряжением на нем соотношением q = CU, то мы можем записать

C ₁U ₁ = C ₂U ₂.

С другой стороны,

U ₁ + U ₂ = U.

Решая совместно эту систему уравнений, найдем напряжение на первом и втором конденсаторе

,

.

Подставляя эти значения в формулу для энергии конденсатора, получим

;

.

Подставим значения величин и получим

W_Э1 = 210^-6 Дж = 2 мкДж, W_Э2 = 110^-6 Дж = 1 мкДж.

6. Медный проводник (удельное сопротивление меди  = 17 нОм·м) подключен к источнику с ЭДС,  = 4 В. Внутреннее сопротивление источника r = 0,1 Ом. Сечение проводника S = 0,085 мм², длина l = 9,5 м. Считая, что ток течет по всему поперечному сечению проводника, найти величину напряженности электрического поля внутри него.