
ТЕСТОВЫЕ ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО КУРСУ ТЭС.
1. Математические модели сигналов и помех
Сигнал не несет информации, если он: 1) случайный; 2) детерминированный; 3) его мощность равна или меньше мощности шума; 4) таков, что в пункте приема часто не удается определить значение переданного сообщения.
Ожидаемое сообщение считается случайным: 1) всегда; 2) лишь если имеются замирания; 3) лишь если имеются помехи; 4) только при передаче в канале без помех.
Для полного вероятностного описания m-ичного символа нужно задать: 1) плотность вероятности; 2) m-мерную плотность вероятности; 3) математическое ожидание и дисперсию; 4) ряд распределения вероятности.
Вероятность совместного появления xj и yk в общем случае определяется по формуле: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
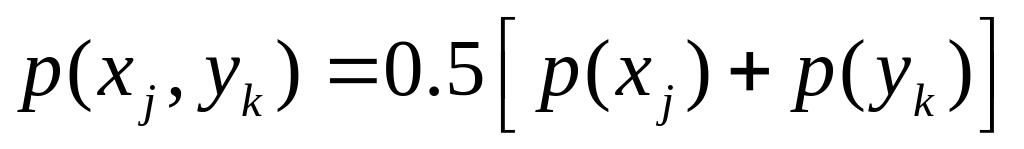 .
.Вероятность появления xj определяется по формуле: 1)
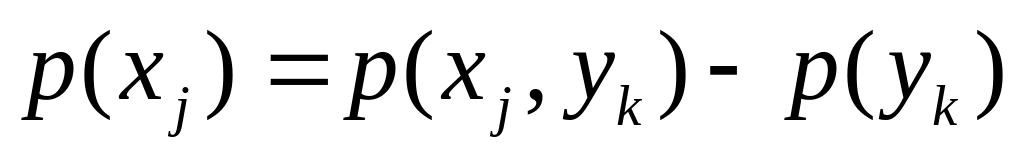 ;
2)
;
2)
 ;
3)
;
3)
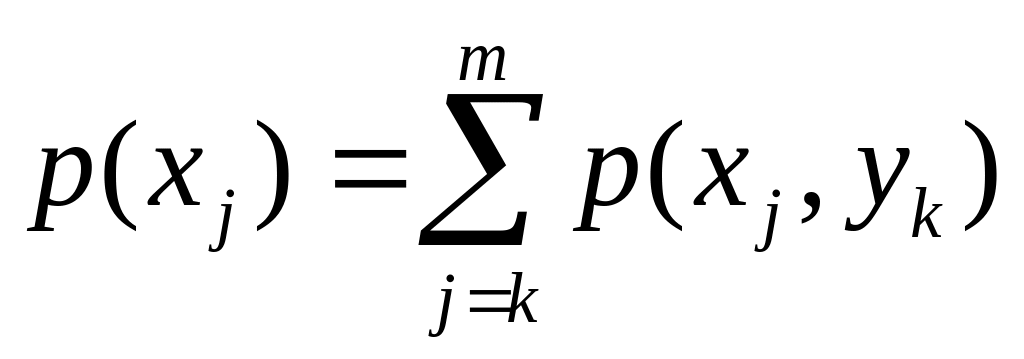 ;
4)
;
4)
 .
.Две дискретные случайные величины X и Y независимы, если при всех j и k: 1)
 2)
2)
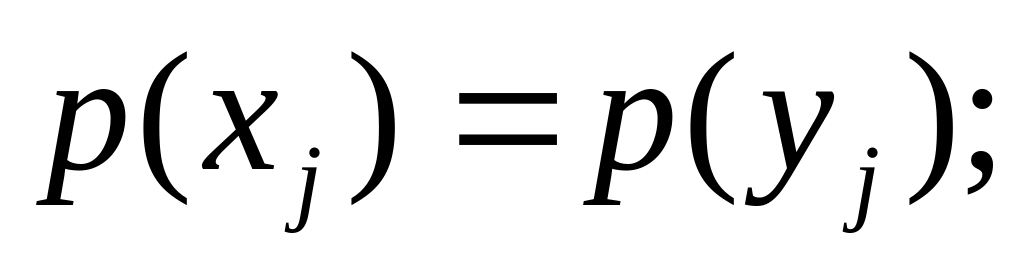 3)
3)
 4)
4)

Для полного вероятностного описания последовательности m-ичных символов длиной n нужно задать: 1) плотность вероятности; 2) nm-мерную плотность вероятности; 3) математическое ожидание и дисперсию; 4) ряд распределения вероятностей реализаций.
Дискретный сигнал это:
1) последовательность m –ичных символов длиной n;;
2) последовательность n непрерывных случайных величин – отсчетов случайного процесса по времени;
3) последовательность двоичных символов;
4) последовательность отрезков случайного процесса.
Для полного вероятностного описания последовательности n отсчетов непрерывного сигнала нужно задать: 1) плотность вероятности каждого отсчета; 2) n-мерную плотность вероятности; 3) математические ожидания и дисперсии; 4) ряд распределения вероятностей реализаций.
Плотность вероятности нормальной случайной величины Х равна: 1)
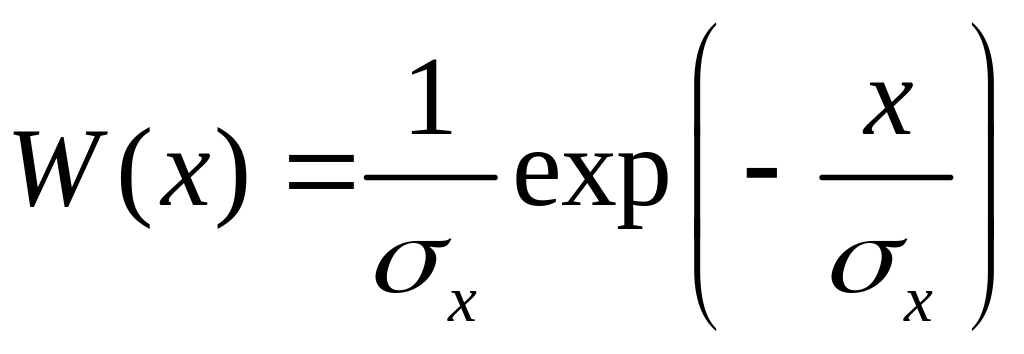 ;
2)
;
2)
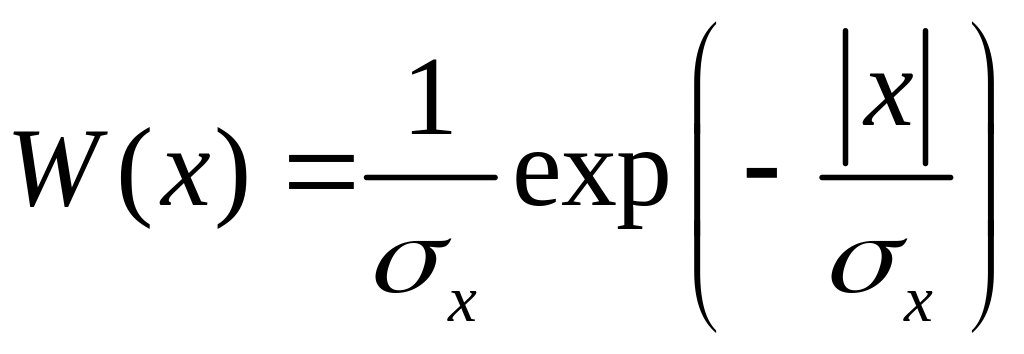 ;
3)
;
3)
 ;
4)
;
4)
 .
.Для полного вероятностного описания отрезка непрерывной случайной функции нужно задать: 1) плотность вероятности каждого отсчета; 2) n-мерную плотность вероятности при n→∞; 3) математические ожидания и дисперсии; 4) ряд распределения вероятностей реализаций.
Для сигнала в виде последовательности двоичных прямоугольных импульсов без пауз (без возвращения к нулю), передаваемых со скоростью 2000 бит/с, укажите минимальную частоту, на которой спектральная плотность мощности обращается в нуль.
1) 1000 Гц.; 2) 4000 Гц; 3) 2000 Гц; 4) 8000 Гц.
2. Преобразования сигналов
Ширина спектра (Гц) стандартного аналогового телефонного сигнала составляет
1) 20 КГц; 2) 3,4 КГц; 3) 8 КГц; 4) 4 КГц.
Укажите минимально возможную частоту квантования по времени (отсчетов/с) телефонного сигнала в соответствии с теоремой отсчетов.
4 КГц;
20 КГц;
6,8 КГц;
8 КГц.
Укажите стандартную частоту квантования во времени (отсчетов/с) телефонного сигнала.
4 КГц;
20 КГц;
22 КГц;
8 КГц.
Укажите стандартное количество уровней по напряжению при АЦП телефонного сигнала.
512;
256;
64;
8.
Укажите количество разрядов в стандартном АЦП, применяемом при преобразовании телефонного сигнала.
64;
52;
128;
8.
Фильтрация аналогового сигнала с помощью ФНЧ перед дискретизацией по времени:
1) позволяет уменьшить шум квантования по уровню;
2) позволяет уменьшить шум дискретизации по времени;
3) позволяет увеличить шаг квантования по уровню;
4) позволяет увеличить шаг дискретизации по времени.
Шум квантования аналогового сигнала по уровню определяется:
1) шириной спектра аналогового сигнала;
2) полосой пропускания ФНЧ;
3) количеством разрядов АЦП;
4) интервалом дискретизации по времени.
Восстановление непрерывного сигнала из последовательности осуществляется с помощью:
1) согласованного фильтра;
2) системы с фазовой автоподстройки частоты;
3) фильтра нижних частот с прямоугольной частотной характеристикой;
4) коррелятора.
При передаче сигнала с понижением скорости ширина его спектра: 1) увеличивается; 2) уменьшается; 3) не меняется; 4) не меняется, но сам спектр сдвигается в область более низких частот.
При передаче двоичной последовательности по радиолинии наибольшая полоса потребуется при использовании: 1) АМ; 2) ЧМ; 3) ФМ; 4) ОФМ.
При передаче двоичной последовательности по радиолинии наименьшая полоса потребуется при использовании: 1) АМ; 2) ФМ; 3) КАМ-4; 4) КАМ-16.
Квадратурно-амплитудная модуляция применяется: 1) для уменьшения битовой вероятности ошибки; 2) для увеличения битовой скорости передачи при использовании той же полосы частот; 3) для повышения надежности синхронизации приемника; 4) чтобы использовать более простой демодулятор.
При передаче непрерывного сигнала используют АМ ОБП:
1) Чтобы использовать более простой модулятор;
2)чтобы уменьшить вероятность ошибки;
3) чтобы упростить демодулятор;
4) для уменьшения требуемой полосы радиолинии.
При передаче непрерывного сигнала по радиолинии наименьшая полоса потребуется при использовании: 1)АМ
2) АМ ОБП 3) ФМ; 4) ЧМ;
