Лабораторная работа № 4 Координатный метод решения геометрических задач. Виды уравнений прямой линии на плоскости

Вопросы по теме

1. Введите понятия: одномерная и двухмерная декартовы системы координат, координаты точки на прямой и на плоскости.

2. Введите понятие трёхмерной системы координат. В чём отличие между правосторонней и левосторонней системами?

3. Сформулируйте задачу о делении отрезка в заданном отношении и опишите координатный метод решения этой задачи.

4. Приведите формулу вычисления расстояния между точками.

5. Приведите формулу вычисления площади треугольника, координаты вершин которого заданы.

Перечислим основные виды уравнений прямой линии на плоскости.

1. Общее уравнение прямой линии: Ax+By+C=0, где A, B, C  параметры прямой, причём, A²+B²≠0.

2. Уравнение прямой линии, проходящей через заданную точку и перпендикулярной заданному вектору: A(xx₀)+B(yy₀)=0, где (x₀, y₀)  координаты точки, через которую проходит прямая, (A, B)  координаты ненулевого вектора, перпендикулярного прямой линии.

3. Нормальное уравнение прямой линии: ax+byp=0, где (a, b)  координаты единичного вектора, перпендикулярного прямой линии, параметр p>0 равен расстоянию от прямой линии до начала координат.

4. Уравнение прямой линии с угловым коэффициентом: y=kx+b, где b  ордината точки, в которой прямая линия пересекает ось ординат, k  угловой коэффициент, равный тангенсу угла наклона между осью абсцисс и прямой линией.

5. Уравнение прямой линии с угловым коэффициентом, проходящей через заданную точку: yy₀=k(xx₀).

6. Уравнение прямой линии, проходящей через две заданные точки: , где (x₁, y₁) и (x₂, y₂)  координаты точек, через которые проходит прямая линия.

7. Параметрическое уравнение прямой линии, проходящей через заданную точку: 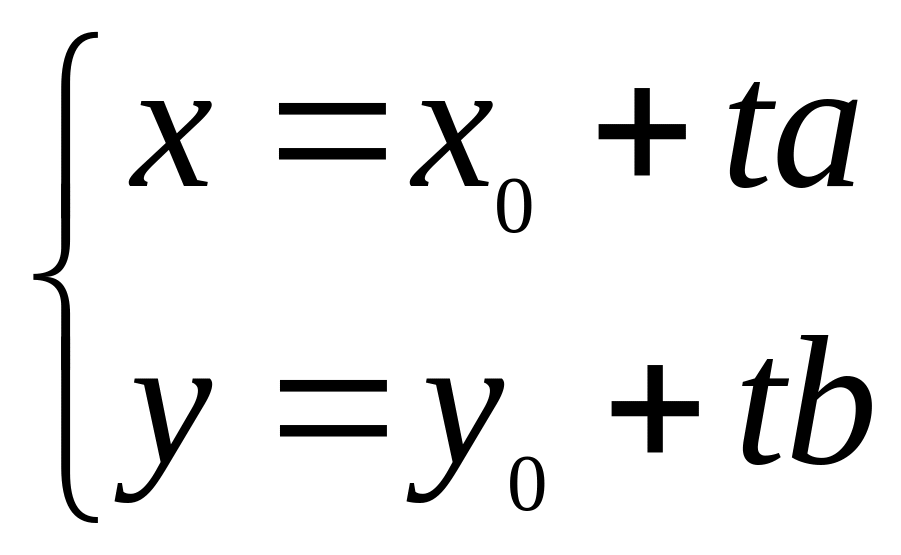, где (a, b)  координаты ненулевого вектора, коллинеарного прямой линии, t∈(∞, +∞).

8. Каноническое уравнение прямой линии, проходящей через заданную точку: .

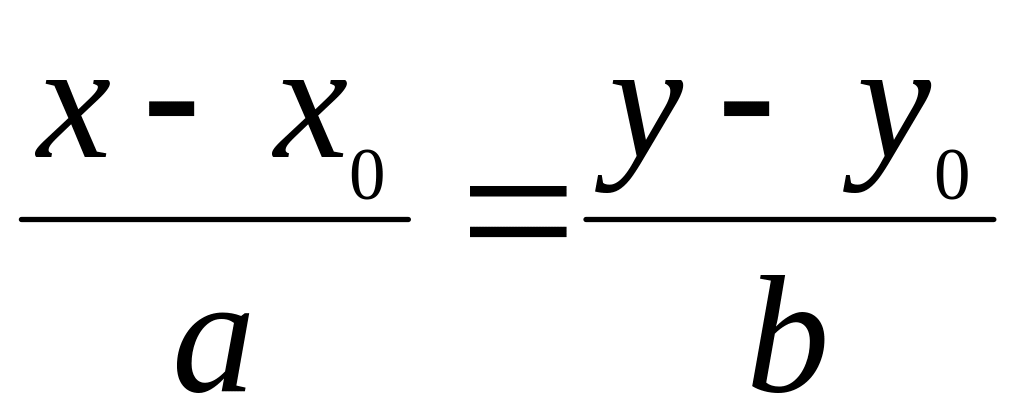9. Уравнение прямой линии в отрезках на осях: , где a  абсцисса точки, в которой прямая линия пересекает ось абсцисс, b  ордината точки, в которой прямая линия пересекает ось ординат.

Примеры решения задач

1. Прямая линия l проходит через точку М₀(2, 5) и перпендикулярна вектору с координатами (8, 3). Записать уравнение этой линии в общем виде, в нормальном виде, в виде уравнения с угловым коэффициентом, в виде уравнения прямой линии в отрезках на осях.

Решение.

Уравнение прямой линии, перпендикулярной заданному вектору и проходящей через заданную точку: l: 8∙(x+2) 3∙(y5)=0.

Раскрыв скобки и приведя подобные слагаемые, получим уравнение в общем виде: l: 8x3y+31=0.

Вычислим длину направляющего вектора, перпендикулярного данной прямой линии: . Разделив уравнение прямой линии в общем виде на , получим нормальное уравнение прямой: l: . В данном уравнении величина равна расстоянию от прямой до начала координат.

Разрешив уравнение прямой в общем виде относительно y, получим уравнение с угловым коэффициентом: l: .

Рассмотрим уравнение в общем виде: l: 8x3y+31=0.

Вычислим координаты точек пересечения прямой линии с осями координат: если y =0, то , если x =0,то . Таким образом, в уравнении прямой линии в отрезках на осях параметры a и b равны: a=31/8, b =31/3. Уравнение имеет вид: .

2. Даны вершины треугольника ABC: B(6; 6), C(6; 2). Угловые коэффициенты прямых, проходящих через стороны AB и AC равны соответственно: k_AB =5/8, k_AC =5/4. Найти: а) уравнения сторон AB, BC, AC; б) координаты вершины A; в) расстояние от точки пересечения медиан до вершины C; г) уравнение медианы СС₁.

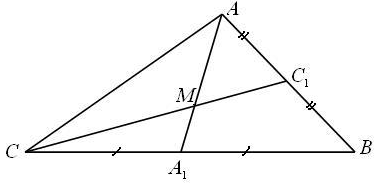
Решение.

а) Уравнения сторон AB и AC найдём, воспользовавшись уравнением прямой линии с угловым коэффициентом, проходящей через заданную точку l: yy₀=k(xx₀).

l_AB: ; l_AC: .

Уравнение стороны BC найдём, воспользовавшись уравнением прямой линии, проходящей через две заданные точки l: .

l_BС: ; l_BС: .

б) Вершина A является точкой пересечения прямых l_AB и l_AC .

Для отыскания координат вершины A решим систему уравнений: . Решим систему с помощью MathCad.

Координаты точки A(24.4; 25).

в) Найдём координаты точки C₁, расположенной в середине отрезка AC:

Вычислим длину медианы CC₁:

.

Так как точка пересечения медиан делит медиану в отношении 2:1, то длина отрезка MC, т.е. расстояние от точки пересечения медиан до вершины C равна

Вычисления в MathCad подтверждают правильность расчётов.

г) Уравнение медианы СС₁ найдём, воспользовавшись видом уравнения прямой линии, проходящей через две заданные точки:

l: . Так как координаты точек С(6; 2) и С₁(15.2; 13.5), то

l_СС1: ; l_СС1: .

Задания для самостоятельной работы

1. Прямая линия l проходит через точку М₀(n, m+n) и перпендикулярна вектору с координатами (nm, m). Записать уравнение этой линии в общем виде, в нормальном виде, в виде уравнения с угловым коэффициентом, в виде уравнения прямой линии в отрезках на осях.

2. Даны вершины треугольника ABC: B(m; m+1), C(m; n). Угловые коэффициенты прямых, проходящих через стороны AB и AC равны соответственно: tg B =m/n, tg C=n/m. Найти: а) уравнения сторон AB, BC, AC; б) координаты вершины A; в) расстояние от точки пересечения медиан до вершины C; г) уравнение медианы СС₁.