Введение
Материалы к каждому практическому занятию содержат краткую теоретическую информацию, примеры выполнения типовых заданий, а также варианты заданий для самостоятельного решения. Задания отличаются выбором параметров в исходных данных.
В таблице 1 предлагаются рекомендуемые значения параметров по вариантам.
Таблица 1.
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
m |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
2 |
4 |
4 |
5 |
4 |
2 |
6 |
n |
5 |
6 |
2 |
1 |
1 |
1 |
6 |
3 |
4 |
4 |
3 |
2 |
3 |
5 |
6 |
2 |
В приложении к практикуму содержатся основные сведения об инструментах MathCad и использовании их для решения предлагаемых задач.
Лабораторная работа № 2 Геометрические векторы и операции над ними
Вопросы по теме
Введите понятия: геометрический вектор, длина вектора, нулевой вектор, коллинеарные и компланарные векторы, свободные векторы.
Как задать координаты вектора в декартовой системе координат?
Дайте определение линейных операций над векторами. Перечислите свойства линейных операций. Как выполнять линейные операции над векторами в координатной форме?
Дайте определение скалярного произведения векторов. Приведите формулу для вычисления скалярного произведения в координатной форме.
Введите понятие ортогональной проекции вектора на заданное направление.
Перечислите свойства скалярного произведения и приведите формулу для вычисления угла между векторами.
Приведите формулу для вычисления длины вектора с помощью скалярного произведения и перечислите свойства длины вектора.
Дайте определение векторного произведения и перечислите его свойства.
Дайте определение смешанного произведения и перечислите его свойства.
П
римеры
решения задач
1. Изобразить в декартовой системе
координат геометрические векторы
и
;
построить вектор
и найти его координаты. Вычислить
координаты вектора
в соответствии с правилами выполнения
линейных операций над векторами,
заданными в координатной форме.
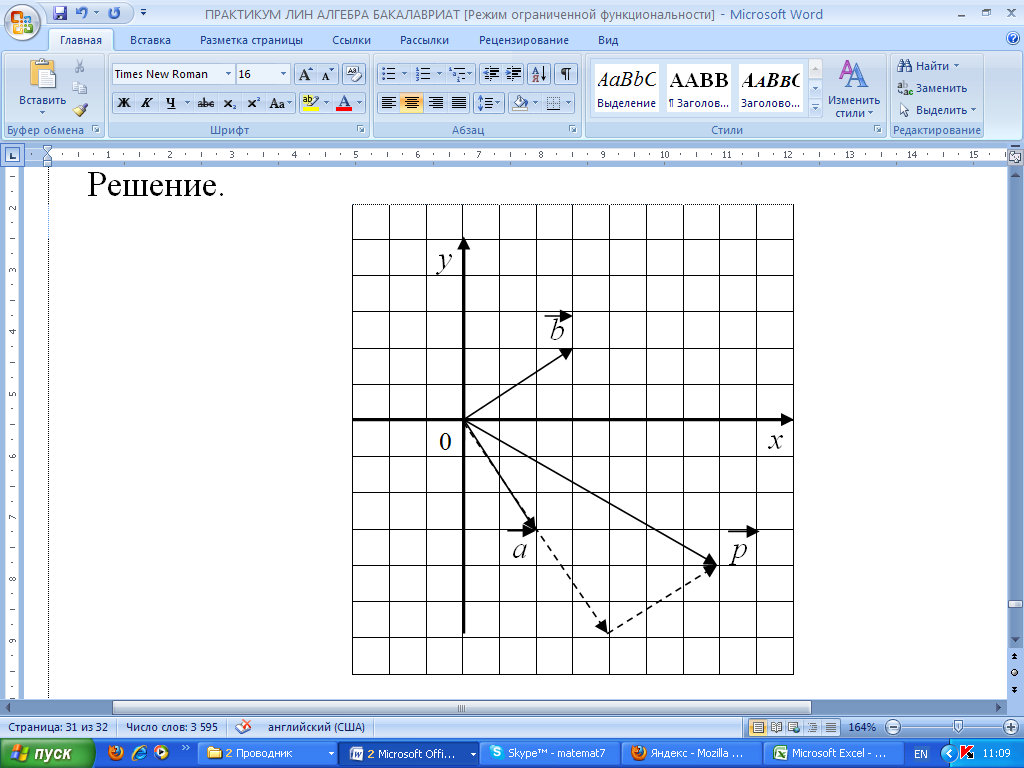
Решение.
Напомним, что
вектор
совпадает по направлению с вектором
и имеет в два раза большую длину. Сумма
векторов
и
построена по правилу «треугольника»,
т.е. начало вектора
параллельным переносом совмещено с
концом вектора
.
В результате получен вектор
.
Координаты этого вектора:
.
Вычислим
координаты вектора
в соответствии с правилами выполнения
линейных операций над векторами,
заданными в координатной форме:
.
Нетрудно убедиться, что результаты построения и вычисления совпадают.
2. Известны:
длина вектора
;
длина вектора
;
угол между этими векторами φ=π/3.
Требуется: а)
длину вектора
;
б) найти угол между диагоналями
параллелограмма, построенного на
векторах
и
;
в)
найти значение λ, при котором векторы
и
будут ортогональны.
Решение.
О
тметим,
что диагонали параллелограмма – это
векторы
и
.
Скалярное произведение векторов равно
произведению длин этих векторов и
косинуса угла между ними.
а)
Длину вектора
вычислим по формуле:
б) Угол α между векторами и вычислим по формуле:
.
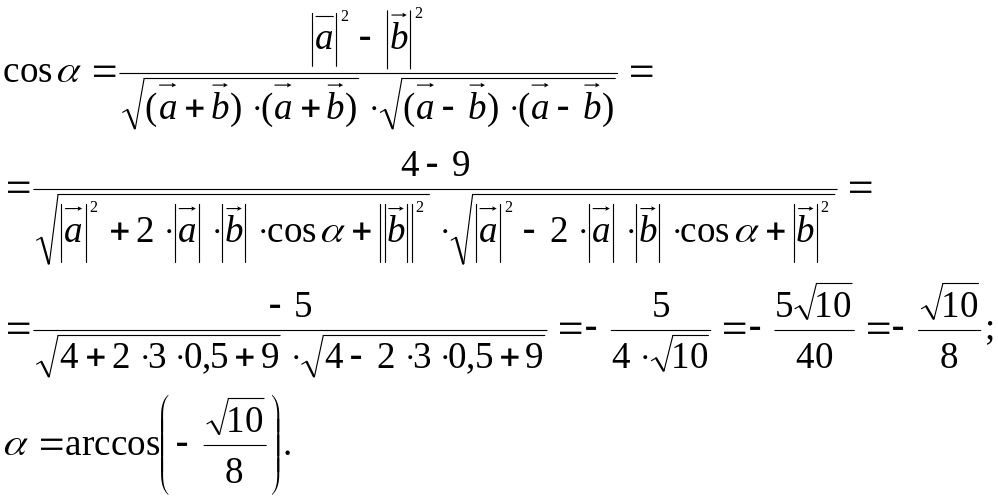
в)
значение λ
найдём из условия ортогональности
векторов, а именно, скалярное произведение
ортогональных векторов равно нулю:
3.
Даны координаты векторов
и
.
Вычислить: длину каждого вектора,
скалярное произведение векторов, угол
φ между векторами, длину вектора
,
пользуясь правилами выполнения операций
над векторами, заданными в координатной
форме. Найти вектор
и смешанное произведение векторов
.
Решение.
;
;
;
;
;
;
Смешанное
произведение векторов
это число, равное скалярному произведению
вектора
на вектор
.
Можно доказать также, что смешанное
произведение равно определителю,
строками которого являются векторы
.
4. Выполнить задания из предыдущего пункта с помощью MathCad.
Вычисления в MathCad.
Заметим, что в среде MathCad векторы должны быть представлены в виде векторов-столбцов.
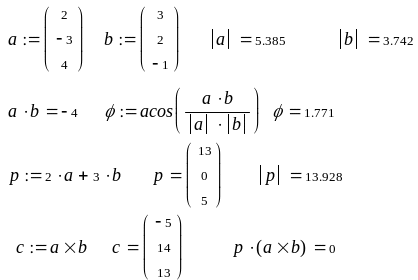
Задания для самостоятельной работы
1. Изобразить в декартовой
системе координат геометрические
векторы
и
;
построить вектор
и найти его координаты. Вычислить
координаты вектора
в соответствии с правилами выполнения
линейных операций над векторами,
заданными в координатной форме.
2. Известны:
длина вектора
;
длина вектора
;
угол между этими векторами φ=π/3.
Требуется: а)
длину вектора
;
б) найти угол между диагоналями
параллелограмма, построенного на
векторах
и
;
в)
найти значение λ, при котором векторы
и
будут ортогональны.
3.
Даны координаты векторов
и
.
Вычислить: длину каждого вектора,
скалярное произведение векторов, угол
φ между векторами, длину вектора
,
пользуясь правилами выполнения операций
над векторами, заданными в координатной
форме. Найти вектор
и смешанное произведение векторов
.
4. Выполнить задания из предыдущего пункта с помощью MathCad.