10

Московский государственный технический

университет им. Н. Э. Баумана.

Калужский филиал.

Т.С. Китаева, а.В. Попов «Определение момента инерции маятника Максвелла»

Методические указания к выполнению лабораторной работы № 4

по курсу механики, молекулярной физики и термодинамики.

Калуга 2007 г.

Правила техники безопасности.

Необходимо выполнять общие правила безопасности труда, относящиеся к устройствам, в которых используется напряжение до 250 .

Эксплуатация установки допускается при наличии заземления. При любых неполадках в установке обращаться к дежурному лаборанту или преподавателю.

Целью данной работы является экспериментальное определение момента инерции маятника Максвелла.

1. Теоретическая часть.

Момент инерции системы материальных точек относительно некоторой неподвижной оси вращения определяется равенством:

, (1)

где - масса -й точки системы;

- расстояние от -й точки до оси вращения.

Для твёрдого тела:

, (2)

где - элемент массы твёрдого тела;

- расстояние от элемента массы до оси вращения;

- элементарный объём;

- расстояние от элементарного объёма до оси вращения;

- плотность вещества тела ( ).

Момент инерции тела относительно произвольно заданной оси вращения определяется с помощью теоремы Штейнера:

, (3)

где - масса тела;

- момент инерции данного тела относительно оси, проходящей через центр масс тела параллельно заданной оси;

- расстояние между указанными осями.

Используя основное уравнение динамики вращательного движения, момент инерции тела относительно неподвижной оси можно вычислить по формуле:

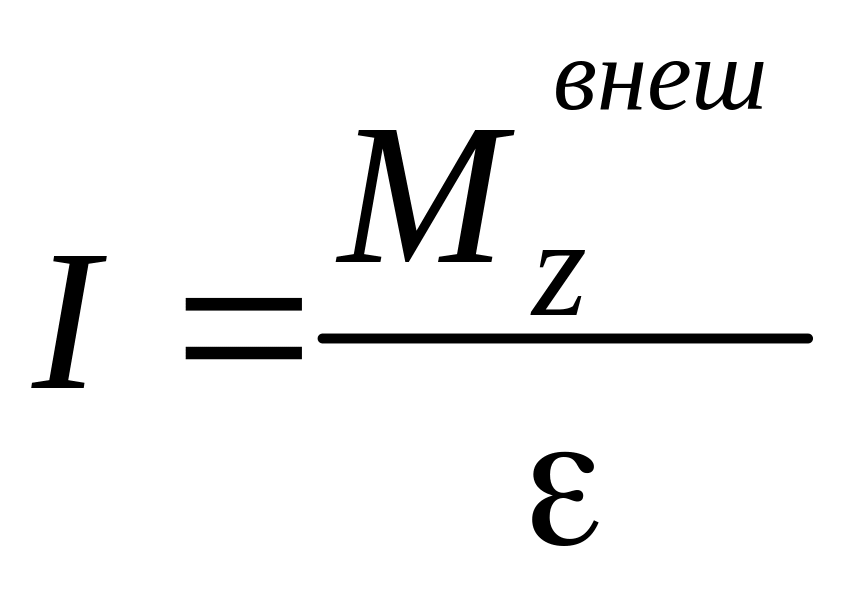, (4)

где - результирующий момент действующих на тело внешних сил относительно данной неподвижной оси;

- угловое ускорение тела.

Момент инерции тела относительно заданной оси и угловая скорость позволяют вычислить кинетическую энергию вращательного движения этого тела:

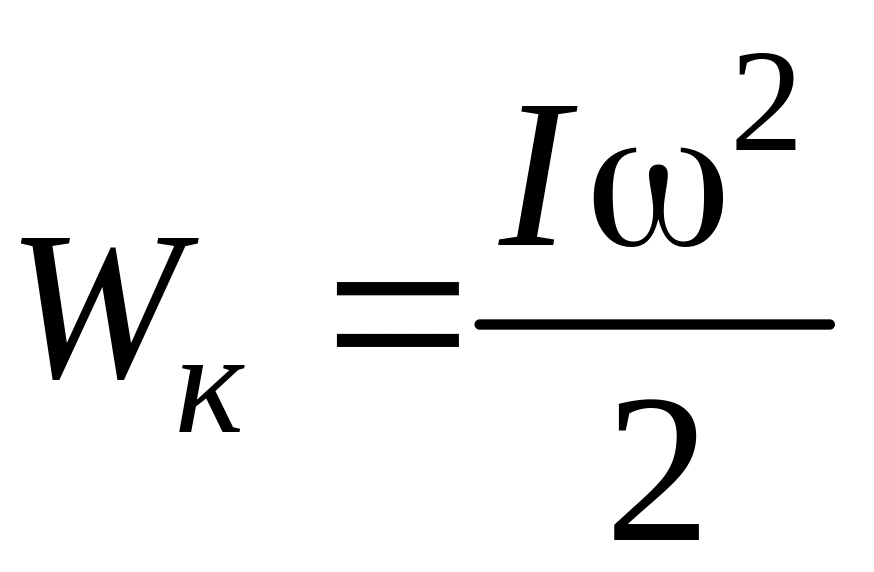(5)

Экспериментальное определение момента инерции маятника Максвелла основано на законе сохранения энергии в механике: полная энергия изолированной консервативной системы - величина постоянная.

М аятник Максвелла (Рис. 1.) представляет собой диск (маховик 1), жестко закреплённый на осевом стержне 2, висящем на двух нитях 3, прикрепленных к опоре 4.

Вращая маятник Максвелла вокруг его оси и тем самым наматывая нити 3 на осевой стержень 2, можно поднять его на некоторую высоту . В этом случае маятник, обладающий массой , будет иметь потенциальную энергию ( - ускорение свободного падения).

Рис. 1. Маятник Максвелла. Предоставленный затем самому себе, маятник начнёт раскручиваться, и его потенциальная энергия начнёт переходить в кинетическую энергию поступательного движения и вращательного движения . Таким образом, на основании закона сохранения механической энергии имеем:

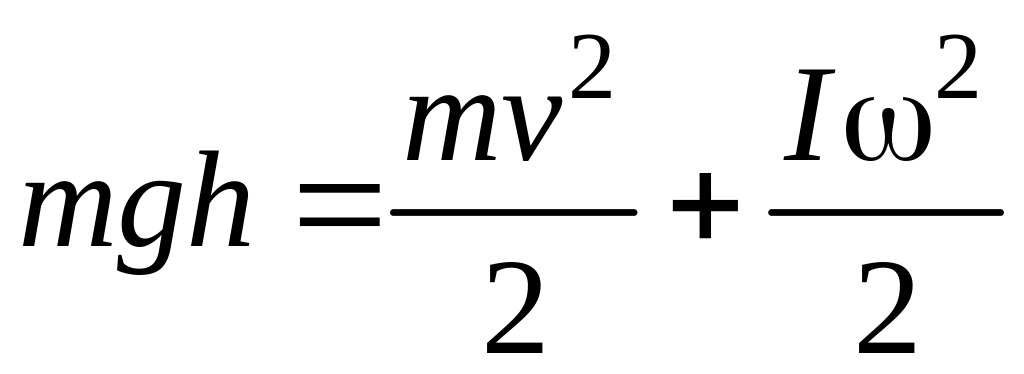, (6)

где - момент инерции маятника относительно его оси вращения;

- высота, на которую опустилась ось маятника;

- скорость спуска оси маятника в тот момент, когда ось опустилась на расстояние ;

- угловая скорость маятника в тот же момент времени.

Из уравнения (6) следует:

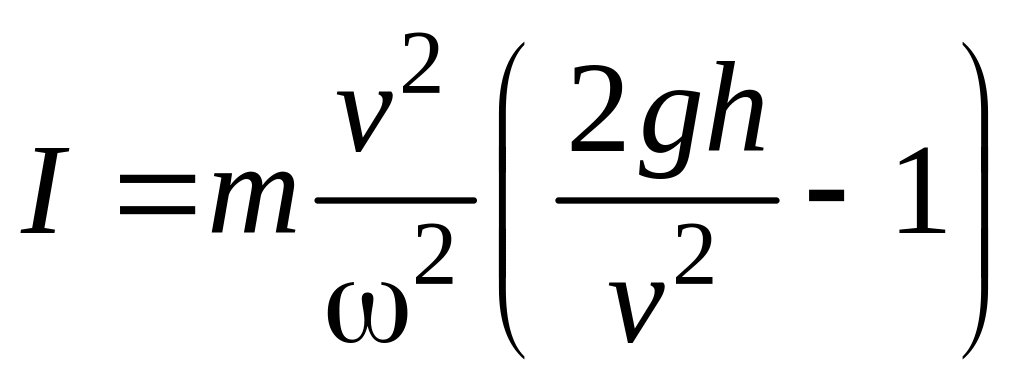(7)

Раскручивание нитей с осевого стержня маятника совершается без их проскальзывания. Поэтому

, (8)

где - радиус осевого сечения стержня;

- диаметр нити.

В тоже время, поскольку маятник опускается с ускорением , не равным ( ), скорость на расстоянии от начального верхнего положения можно определить с использованием зависимости:

(9)

Подставим (8) и (9) в (7). Тогда момент инерции равен:

(10)

Учитывая, что , , окончательно получим:

, (11)

где - диаметр осевого стержня, ;

- диаметр нити, ;

- время спуска оси маятника на расстояние ;

- масса маятника;

- ускорение свободного падения.

С другой стороны, теоретическое значение момента инерции маятника Максвелла можно рассчитать по формуле как сумму моментов инерции составляющих его отдельных элементов:

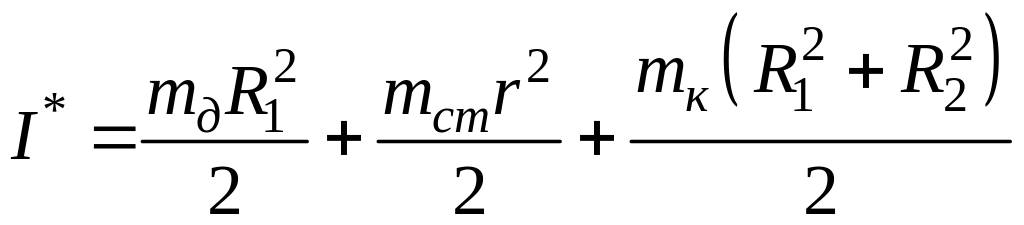, (12)

где - масса диска (маховика 1) маятника, включая массу части осевого стержня 2 внутри его;

- масса части осевого стержня вне маховика;

- масса кольца 5;

- радиус осевого стержня, ;

, - внутренний и внешний радиусы кольца, , .