БФИ 19-01 / ВТФЭ / 3 лаба

Министерство науки и высшего образования Российской Федерации Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева

ОПРЕДЕЛЕНИЕ ВИДИМОЙ УГЛОВОЙ СКОРОСТИ СПУТНИКА ПО НАЗЕМНЫМ ФОТОГРАФИЧЕСКИМ НАБЛЮДЕНИЯМ

Методические указания к выполнению лабораторной работы по курсу «Введение в технику физического эксперимента» для студентов бакалавриата

по направлению подготовки 03.03.02 «Физика» очной формы обучения

Красноярск 2019

УДК 521.1-13:629.78

Рецензент кандидат физ.-мат. наук, доцент А. Ю. Игуменов

(Сибирский государственный университет науки и технологий имени академика М.Ф. Решетнева)

Печатается по решению редакционно-издательского совета университета

Определение видимой угловой скорости спутника по наземным фото-

графическим наблюдениям: метод. указания к выполнению лаб. работы по курсу «Введение в технику физического эксперимента» для студентов бакалавриата по направлению 03.03.02 «Физика» очной формы обучения / сост.: Владимиров В. М., Лапухин Е. Г., Вайтузин О. П.; СибГУ им. М. Ф. Решетнева – Красноярск, 2019. – 12 с.

© СибГУ им. М.Ф. Решетнева, 2019

2

ОБЩИЕ СВЕДЕНИЯ

Определение видимой угловой скорости спутника по фотографическим наблюдениям и наблюдениям с помощью ПЗС-камеры сводится к определению видимого углового расстояния между двумя положениями спутника на определенные моменты времени. Отношение углового расстояния к времени пролета однозначно определяет видимую угловую скорость спутника.

Методические указания содержат теоретические сведения о небесных системах координат, используемых в астрономии и геодезии, и об основных операциях сложения и вычитания углов на небесной сфере из курса сферической геометрии. Экспериментальная часть включает в себя описание оборудования для получения снимков и краткое описание определения экваториальных координат положения спутника в программе MaxIm DL.

В методические указания включены контрольные вопросы и список литературы, необходимый для более глубокого изучения материалов по данной тематике.

Издание предназначено для студентов направления «Физика» очной формы обучения, но также может быть полезно магистрам, аспирантам и преподавателям, имеющих дело с определением видимой угловой скорости космического аппарата.

Лабораторная работа

ОПРЕДЕЛЕНИЕ ВИДИМОЙ УГЛОВОЙ СКОРОСТИ СПУТНИКА ПО НАЗЕМНЫМ ФОТОГРАФИЧЕСКИМ НАБЛЮДЕНИЯМ

Цель работы: определить видимую угловую скорость космического аппарата по данным ПЗС-снимка.

Задачи работы:

-ознакомиться с различными системами координат и шкалами времени, используемых в астрономии и геодезии;

-ознакомиться с оборудованием для получения ПЗС-изображения с треком космического аппарата;

-научиться определять координаты начала и конца трека спутника на изображении, длину трека и видимую угловую скорость.

Краткие теоретические сведения

Небесные координаты. При изучении видимых движений небесных тел необходимо определять их положения в моменты наблюдений. При этом нет необходимости знать расстояния до них, поскольку все тела представляются нам как бы находящимися на внутренней поверхности некоторой сферы произвольного радиуса. Поэтому видимые, положения светил можно опреде-

3

лять только направлениями, а их взаимное расположение – углами между этими направлениями, или соответствующими дугами больших кругов на сфере, из центра которой исходят все направления.

Небесная сфера – гипотетическая сферическая поверхность произвольного радиуса, в центре которой помещается наблюдатель, на которую проецируются небесные светила.

На небесной сфере вводят различные системы небесных координат для описания положений и движений небесных тел.

Положение светила на небе однозначно определяется по отношению к основным плоскостям и связанным с ними линиям и точкам небесной сферы и выражается количественно двумя величинами (центральными углами или дугами больших кругов), которые называются небесными координатами.

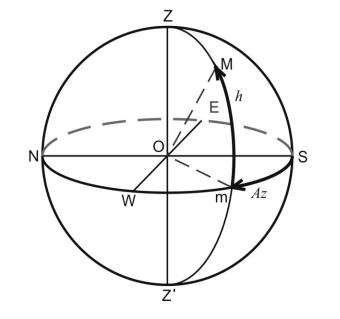
Горизонтальная система координат. Основной плоскостью в этой системе является плоскость математического горизонта NESW с центром O на поверхности Земли (рис. 1), а отсчет ведется от зенита Z (или от плоскости горизонта) и от одной из точек математического горизонта.

Рис. 1. Горизонтальная топоцентрическая система координат: M – объект на небесной сфере; N, E, S, W – точки севера, востока, юга и запада; Z и Z′ – зенит и надир

Одной координатой является или зенитное расстояние z (дуга ZM на рис. 1, равная углу ZOM), или высота светила над горизонтом h (дуга mM от математического горизонта до точки M равная углу mOM). Зенитные расстояния отсчитываются в пределах от 0° до 180° в направлении от зенита Z к надиру Z′. Светила, находящиеся в видимой части небесной сферы, имеют z < 90°, а в невидимой части z > 90°. Высоты h изменяются от 0° до +90° к зениту и от 0° до -90° ниже плоскости горизонта. Высота, или зенитное расстояние, определяет положение объекта на вертикальном круге Z′mMZ.

4

Положение вертикального круга на небесной сфере определяется другой координатой – азимутом Аz. Азимутом Аz светила М называется дуга математического горизонта Sm от точки юга S до вертикального круга, проходящего через светило, или центральный угол SOm (в плоскости математического горизонта.

Азимуты отсчитываются к западу W от точки юга S, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу (западные азимуты) и от 0° до -180° (восточные азимуты).

В геодезии азимуты отсчитываются от точки севера N. Такие азимуты называются геодезическими, в отличие от астрономических азимутов, отсчитываемых от точки юга.

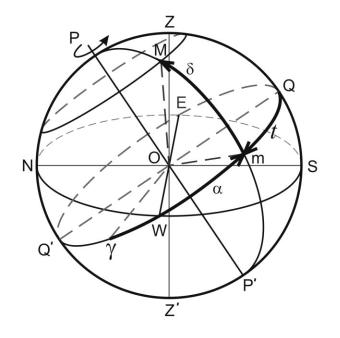
Первая экваториальная система координат. Основной плоскостью в этой системе является плоскость небесного экватора QWQ'E, а началом отсчета – точки небесного экватора (рис. 2). Ось PP′ называется осью мира.

Рис. 2. Экваториальная система координат:

M – объект на небесной сфере; N, E, S, W – точки севера, востока, юга и запада; Z и Z′- зенит и надир; Q и Q′ – верхняя и нижняя точки экватора; PP′– ось мира

Одной координатой светила M является склонение светила δ. Склонением δ светила М называется дуга mМ часового круга РМmР' от

небесного экватора до светила, или центральный угол mОМ.

Склонение, или полярное расстояние, определяет положение светила на часовом круге. Положение часового круга на небесной сфере определяется другой координатой – часовым углом t.

Часовым углом t светила М называется дуга небесного экватора Qm от верхней точки Q небесного экватора до часового круга РМmР', проходящего через светило, или центральный угол QOm (в плоскости небесного экватора),

5

измеряющий двухгранный угол между плоскостями небесного меридиана и часового круга светила.

Часовые углы отсчитываются в сторону суточного вращения небесной сферы, т.е. к западу от верхней точки Q небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу (западные часовые углы) и от 0° до -180° (от 0h до -12h) к востоку (восточные часовые углы).

Вторая экваториальная система координат. Основной плоскостью в этой системе является также плоскость небесного экватора, а одной координатой – склонение δ (реже – полярное расстояние р).

Другой же координатой, определяющей положение часового круга светила, является прямое восхождение α.

Прямым восхождение α светила М называется дуга небесного экватора γm (см. рис. 2) от точки весеннего равноденствия γ до часового круга, проходящего через светило, или центральный угол γОm (в плоскости небесного экватора) между направлением на точку весеннего равноденствия и плоскостью часового круга светила.

Прямые восхождения α отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере).

Горизонтальные координаты (z, h, А) и часовой угол светила t непрерывно изменяются вследствие суточного вращения небесной сферы, так как они отсчитываются от неподвижных точек, не участвующих в этом вращении.

Экваториальные координаты светила (прямое восхождение α и склонение δ) при суточном вращении небесной сферы не меняются, так как они отсчитываются от точек небесного экватора, которые сами участвуют в суточном вращении, и следовательно, положение светила относительно этих точек не изменяется.

Таким образом, для разных задач используются различные систему координат.

Горизонтальная система координат используется для непосредственных определений видимых положений светил с помощью угломерных инструментов.

Первая экваториальная система (склонение и часовой угол) используется преимущественно при определении точного времени – одной из основных задач практической астрономии.

Вторая экваториальная система является основной при решении задач фундаментальной астрометрии. В этой системе составляются списки звездных положений (звездные каталоги) и звездные карты.

6

Основные определения и формулы сферической геометрии

Геометрические построения и вычисления на поверхности сферы отличаются от таковых на плоскости. Следует заметить, что формулы сферической геометрии справедливы не только для небесной сферы, но и для любой другой сферы (например, при проведении вычислений на земном глобусе). Необходимо лишь учитывать радиус сферы.

Одними из основных понятий планиметрии являются понятия точки и прямой линии. В сферической геометрии аналогом прямой линии как линии с наименьшей длиной, соединяющей две точки, является дуга окружности, образованной пересечением плоскости, проходящей через центр сферы, со сферой. Так как круг – это часть плоскости, ограниченная окружностью, то дадим следующие определения. Любая плоскость, которая проходит через центр сферы и ограничена сферой, называется большим кругом. Любая плоскость, которая не проходит через центр сферы и ограничена сферой,

называется малым кругом.

Как большой, так и малый круг пересекает сферу по окружности. Очевидно, что любая прямая, лежащая в плоскости большого круга и проходящая через центр сферы, является диаметром сферы. Следовательно, два больших круга пересекаются по диаметру сферы.

Через любые две точки, лежащие на поверхности сферы, можно провести большой круг, и дуга окружности между этими точками является кратчайшим расстоянием между ними на сфере. Это утверждение эквивалентно аксиоме из планиметрии: через любые две точки можно провести прямую линию.

Перпендикуляр к большому кругу, проходящий через центр сферы, пересекает ее в двух точках, называемых полюсами.

Рассмотрим сферу с центром в точке O (рис. 3).

Рис. 3. Определение двугранного угла

7

Проведем большой круг через две точки A и B, лежащие на поверхности сферы, затем проведем перпендикуляр к большому кругу.

Полюсы обозначим как P и Z. Через точки P и A, затем через P и B проведем два больших круга. Угол φ между двумя большими кругами называется двугранным углом.

Единицами измерения углов в астрономии являются градусы, радианы, часы. Так как радиус сферы равен единице, то длина дуги ˆAB (рис. 3) равна

центральному углу AOB, то есть φ, выраженному в радианах. По опреде-

лению 1 градус (1º) – это центральный угол, равный 1/360 части окружности. Градус делится на 60 угловых минут (1º = 60ʹ), каждая из которых равна 60 угловым секундам (1ʹ = 60ʺ), то есть градус состоит из 3600 угловых секунд.

Для измерения углов используются также часы, причем (1h) – это центральный угол, соответствующий 1/24 части окружности. В одном часе содержится 60 минут или 3600 секунд (1h = 60m = 3600s). Очевидно, что 1h = 15º, 1m = 15ʹ, 1s = 15ʺ. Пример перевода углов прямого восхождения и склонения в радианную меру приведен в приложении А.

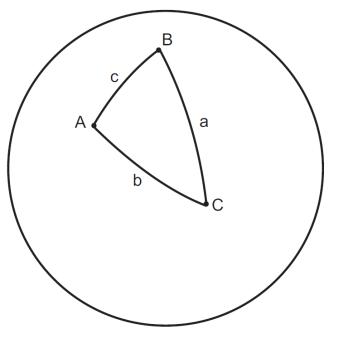
Рассмотрим теперь три точки, которые лежат на сфере и не принадлежат одному большому кругу. Через каждую пару точек можно провести большие круги (рис. 4).

Сферическим треугольником называется фигура, образованная тремя дугами окружностей больших кругов, попарно соединяющих три точки.

Примерами сферических треугольников могут быть треугольники

ABP, ABZ (рис. 3) и ABC (рис. 4).

Рис. 4. Определение сферического треугольника

Обычно углы сферического треугольника обозначают большими буквами, например A, B, C (и являются двугранными углами, которые образуют стороны сферического треугольника), а стороны, противолежащие углам –

8

соответствующими малыми буквами: AB c , BC a , AC b (рис. 4) (являются углами лежащими в одной из плоскостей двугранного угла, например a BOC , b AOC, c AOB , где О – является центром сферы). Как и в планиметрии, в сферической геометрии существуют определенные соотношения между сторонами и углами треугольников.

Здесь отметим лишь следующие свойства сферических треугольников. Углы A и B в треугольнике ABP (рис. 3) – прямые, так как большие круги, проходящие через точки P, A, Z и P, B, Z, перпендикулярны плоскости AOB. Поэтому, поскольку угол φ > 0, сумма углов сферического треугольника может превышать 180º. Теперь проведем плоскость через точки A, B, C (рис. 4), лежащие на сфере, и параллельно ей плоскость, которая проходит через центр сферы. Очевидно, что вторая плоскость поделит сферу на две полусферы, причем треугольник ABC будет полностью лежать в одной из полусфер. Таким образом, любой из углов сферического треугольника будет меньше

180◦.

В пределе (при увеличении каждого из углов до 180º) сферический треугольник трансформируется в полусферу.

Следующие свойства сферического треугольника аналогичны свойствам плоского треугольника:

а) в каждом сферическом треугольнике против большего угла лежит большая сторона;

б) сумма любых двух сторон больше третьей стороны.

Для решения многих задач оказывается удобнее вместо декартовой системы использовать сферическую систему координат.

Рис. 5. Определение сферических координат точки

Сферические координаты (рис. 5): r – радиус-вектор объекта, – полярное расстояние, которое иногда называют коширотой, и – долгота связаны с декартовыми координатами x, y, z уравнениями:

9

Полярное расстояние (коширота) изменяется от 0º до 180º, долгота – от 0º до 360º. Вместо полярного расстояния часто используется широта , при-

чем = 90 - .

Система уравнений (1) представляет преобразование между сферической и декартовой системами координат. Следовательно, связь между координатами будет следующая:

Основные формулы сферической геометрии

Рассмотрим сферический треугольник ABC на небесной сфере, причем точка A является полюсом, а точка B лежит в плоскости Oxz (рис. 6).

Рис. 6. К выводу формул синусов и косинусов

Декартовы координаты единичных векторов rA, rB, rC определяются согласно (1) при

rA 0,0,1 ,

10