5.4. Замена переменной в определенном интеграле

Пусть нужно найти интеграл 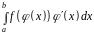, который непосредственно вычислить нельзя, где подынтегральная функция непрерывная.

Допустим, что .

Тогда: , где , .

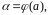
Пример 4. Вычислить .

Решение.

В интеграле была сделана замена:

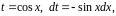и при , , а при .

Рассмотрим еще один случай замены переменной.

Пусть функция непрерывна на отрезке .

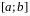Тогда, если:

1) функция 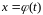дифференцируема на и отображает на , непрерывна на ;

2) функция определенная и непрерывная на ;

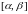3) ; , то справедлива формула: , которая носит название формулы замены переменной в определенном интеграле.

Заметим, что если при вычислении неопределенного интеграла с помощью замены переменной мы должны были вернуться от новой переменной к переменной , то при вычислении определенного интеграла этого можно не делать, достаточно установить новые пределы интегрирования 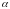и для переменной .

Пример 5. Вычислить .

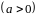Решение.

Если положить 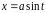, то

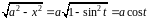и

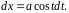
Изменяем пределы интегрирования: при при . Следовательно:

.

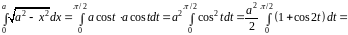
Здесь использована формула: .

5.5. Интегрирование по частям

Известно, что так же, как и для неопределенного интеграла, для определенного интеграла будет справедливой формула интегрирования по частям.

Теорема. Пусть функции и дифференцируемые функции по своим аргументам , тогда:

,

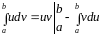где 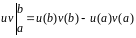, а интеграл 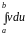будет более проще при интегрировании, чем исходный.

Формула является формулой интегрирования по частям в определенном интеграле.

Пример 6. Вычислить .

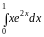Решение.

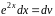Пусть , тогда , , тогда .

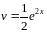Используя формулу интегрирования по частям (19.25), получим:

.

Пример 7. Вычислить .

Решение.

Пусть , тогда , а , тогда .

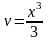Следовательно,

Лекция 6. Определенный интеграл

6.1. Геометрические приложения определенного интеграла

Вычисление длины дуги кривой

Длиной дуги называется предел длины вписанной ломаной линии при неограниченном уменьшении длины ее участков.

Найдем длину дуги 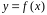, где – непрерывная дифференцируемая функция на .

Длина дуги кривой, которая ограничена , будет:

где . (1)

Если кривая задана уравнениями в параметрической форме то длина дуги кривой определяется по формуле:

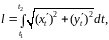(2)

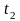где и – значения параметра, которые соответствуют концам дуги.

Если дуга задается уравнением в полярных координатах, то длина дуги определяется:

(3)

где и – значения полярного угла, которые соответствуют концам дуги (в полярной системе координат положение точки на плоскости определяется ее расстоянием 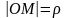от полюса 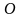и полярным углом, образованным отрезком с полярной осью ).

Прямоугольные и полярные координаты связаны следующими формулами: .

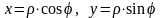Пример 1. Найти длину дуги кривой

Решение.

Чтобы найти пределы интегрирования, найдем область определения заданной функции, решив систему неравенств:

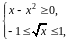
Найдем:

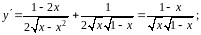
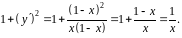
Следовательно: .

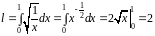Пример 2. Найти длину дуги астроиды (рис. 1).

Решение.

Найдем длину всей дуги,

которая расположена в первой четверти.

Параметр изменяется от

до

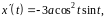
Рис. 1

Получаем:

.

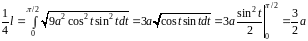Следовательно, длина астроиды .
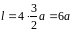