
- •Лекция 1. Неопределенный интеграл
- •1.1. Понятие первообразной функции и неопределенного интеграла
- •Свойства неопределенного интеграла
- •1.2. Таблица основных интегралов. Правила интегрирования
- •1.3. Непосредственное интегрирование
- •Лекция 2. Неопределенный интеграл
- •2.1. Замена переменной в неопределенном интеграле
- •2.2. Интегрирование по частям
- •Лекция 3. Неопределенный интеграл
- •3.1. Интегрирование рациональных дробей
- •3.2. Интегрирование выражений, содержащих квадратный трехчлен
- •3.3. Разложение дроби на простейшие
- •Лекция 4. Неопределенный интеграл
- •4.1. Интегрирование иррациональных выражений
- •4.2. Интегрирование выражений, которые содержат тригонометрические функции
- •Лекция 5. Определенный интеграл
- •5.1. Интегральные суммы. Условия существования определенного интеграла
- •5.2. Свойства определенного интеграла
- •5.3. Вычисление интеграла. Формула Ньютона – Лейбница
- •5.4. Замена переменной в определенном интеграле
- •5.5. Интегрирование по частям
- •Лекция 6. Определенный интеграл
- •6.1. Геометрические приложения определенного интеграла
- •Вычисление площадей геометрических фигур
- •Вычисление объема тела вращения
- •6.2. Использование интегралов в некоторых экономических задачах
Лекция 5. Определенный интеграл
5.1. Интегральные суммы. Условия существования определенного интеграла
Пусть
неотрицательная функция
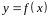 определена и
непрерывная на отрезке
определена и
непрерывная на отрезке
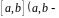 конечные числа).
График функции изображен на рис. 1.
конечные числа).
График функции изображен на рис. 1.
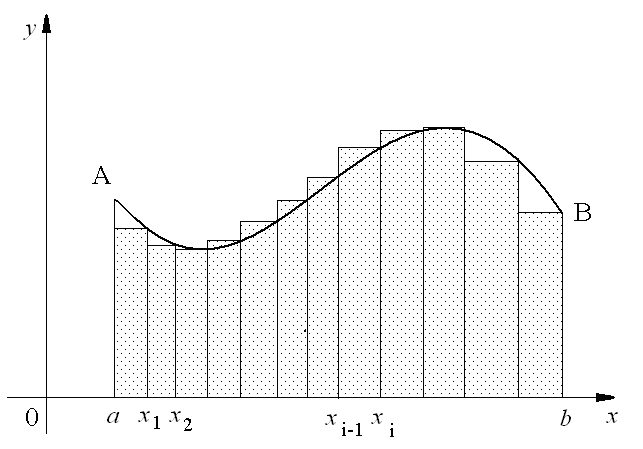
Рис. 1
1. Задача о вычислении площади криволинейной трапеции.
Пусть
плоская фигура ограничена
графиком функции
,
осью
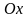 ,
прямыми
,
прямыми
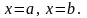
Фигура
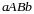 называется криволинейной
трапецией. Для
того
чтобы решить задачу
выполним следующие действия:
называется криволинейной
трапецией. Для
того
чтобы решить задачу
выполним следующие действия:
1)
разобьем произвольно
отрезок
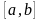 на
частей точками
на
частей точками
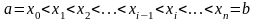 ;
;
2)
выберем на каждом из отрезков
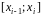 произвольную точку
произвольную точку
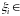
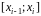 .
Обозначим через
.
Обозначим через
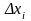 разницу
разницу
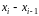 ,
которую будем называть длиной частного
отрезка
;
,
которую будем называть длиной частного
отрезка
;
3)
в точках
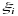 вычислим значение
функции
вычислим значение
функции
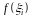 и составим такую сумму:
и составим такую сумму:
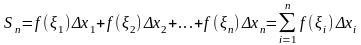 .
.
Геометрический
смысл этой суммы очевиден –
это сумма площадей
прямоугольников с основаниями
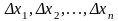 и высотами
и высотами
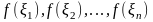 ;
;
4)
для нахождения площади криволинейной
трапеции допустим, что
количество точек
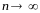 ,
а максимальная длина отрезков стремится
к нулю, то есть
,
а максимальная длина отрезков стремится
к нулю, то есть
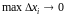 .
.
Тогда
площадь
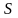 криволинейной фигуры,
которая изображена на
рис.1, есть
предел интегральной суммы,
то есть:
криволинейной фигуры,
которая изображена на
рис.1, есть
предел интегральной суммы,
то есть:
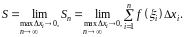
2. Задача о вычислении пути материальной точки.
Пусть
известна скорость движения материальной
точки как функция времени
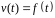 .
Найти путь, который пройдет точка за
время от
.
Найти путь, который пройдет точка за
время от
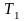 до
до
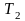 .
Если скорость
не изменяется в течение
времени, то
есть
.
Если скорость
не изменяется в течение
времени, то
есть
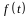 – постоянная
величина, то
путь
– постоянная
величина, то
путь
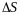 ,
который прошла точка за промежуток
времени
,
который прошла точка за промежуток
времени
 ,
вычисляется по формуле
,
вычисляется по формуле
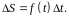
Выполним такие действия:
разобьем отрезок
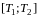 на промежутки времени:
на промежутки времени:
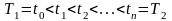 ;
;
2)
на каждом отрезке времени
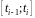 возьмем произвольную точку
возьмем произвольную точку
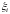 и вычислим в этой точке значения скорости
и вычислим в этой точке значения скорости
 ;
;
3)
для длины пути
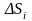 ,
который прошла точка за промежуток
,
который прошла точка за промежуток
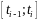 имеем
имеем
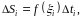 где
где
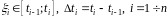 .
.
Тогда
полная длина пути
 ,
если на каждом промежутке времени
,
если на каждом промежутке времени
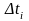 допустить движение равномерным, будет:
допустить движение равномерным, будет:
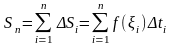 ; 4)
для нахождения пути, который прошла
точка за время от
до
,
найдем предел
при
; 4)
для нахождения пути, который прошла
точка за время от
до
,
найдем предел
при
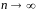 и при
и при
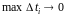 :
:
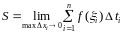 .
.
3. Задача об объеме продукции.
Пусть
функция
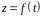 описывает
зависимость
производительности труда
описывает
зависимость
производительности труда
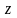 некоторого производства за время
.
Найдем
объем продукции
,
изготовленной за промежуток времени
некоторого производства за время
.
Найдем
объем продукции
,
изготовленной за промежуток времени
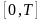 .
Если производительность
не меняется
на протяжении времени, то
есть
.
Если производительность
не меняется
на протяжении времени, то
есть
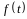 – постоянная величина,
то объем
продукции
– постоянная величина,
то объем
продукции
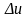 ,
изготовленной за
промежуток времени
,
изготовленной за
промежуток времени
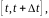 вычисляется
по формуле
вычисляется
по формуле
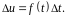 Используя приближенное
равенство
Используя приближенное
равенство
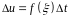 ,
где
,
где
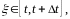 которое будет более точным,
чем
меньшим
будет
которое будет более точным,
чем
меньшим
будет
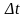 .
Выполним следующие действия:
.
Выполним следующие действия:
1. Разобьем отрезок на промежутки времени:
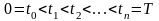 .
.
2.
Вычислим объем продукции
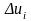 ,
изготовленной за
промежуток
,
изготовленной за
промежуток
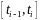 ,
имеем:
,
имеем:
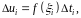 где
где
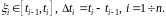
3.
Определим приближенно объем продукции,
изготовленной за промежуток времени
:
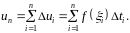
4.
Найдем предел
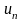 ,
если
,
если
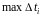 стремится к нулю, а
и получим объем продукции, изготовленной
за промежуток времени
:
стремится к нулю, а
и получим объем продукции, изготовленной
за промежуток времени
:
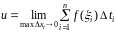 .
.
Итак, рассматривая различные по характеру задачи, пришли к пределу одного вида.
Будем
считать, что на промежутке
задана непрерывная функция
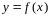 и для нее аналогично рассмотренным
задачам составлена сумма
и для нее аналогично рассмотренным
задачам составлена сумма
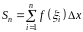 ,
которую будем называть интегральной
суммой для функции
,
которую будем называть интегральной
суммой для функции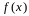 на промежутке
.
на промежутке
.
Если
существует конечный предел интегральной
суммы
при
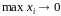 и
и
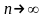 ,
который не зависит от способов разбиения
отрезка на части, а также выбора точек
,
который не зависит от способов разбиения
отрезка на части, а также выбора точек
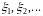 ,
то этот предел называется определенным
интегралом от функции
,
то этот предел называется определенным
интегралом от функции
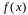 на отрезке
и обозначается:
на отрезке
и обозначается:
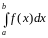
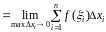 ,
при этом сама функция
,
при этом сама функция
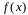 называется подынтегральной функцией,
заданной на отрезке
.
Числа
называется подынтегральной функцией,
заданной на отрезке
.
Числа
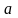 и
и
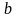 соответственно называются верхним
и нижним пределами интеграла,
соответственно называются верхним
и нижним пределами интеграла,
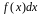 – подынтегральным выражением,
– переменной интегрирования.
– подынтегральным выражением,
– переменной интегрирования.
Отметим,
что поскольку определенным интегралом
является предел интегральной суммы, то
для существования такого предела, а
поэтому и интеграла, достаточно
непрерывности функции
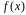 .
.
Заметим
также, что поскольку из определения
определенного интеграла также вытекает,
что величина интеграла зависит от вида
функции
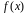 и пределов интегрирования, то определенный
интеграл определяется однозначно и в
отличие от неопределенного интеграла
является числом, которое не зависит от
того, какой буквой обозначается переменная
интегрирования.
и пределов интегрирования, то определенный
интеграл определяется однозначно и в
отличие от неопределенного интеграла
является числом, которое не зависит от
того, какой буквой обозначается переменная
интегрирования.
Следовательно,
можно записать:
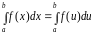 .
.
Геометрический
смысл определенного интеграла: если
функция неотрицательна на отрезке
,
где
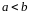 ,
то
,
то
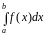 – численно равен площади
криволинейной трапеции, которая
ограничена кривой
– численно равен площади
криволинейной трапеции, которая
ограничена кривой
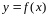 ,
отрезком
и прямыми
,
отрезком
и прямыми
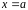 и
и
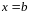 .
.
Физический
смысл определенного интеграла:
определенный интеграл
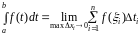 – это длина пути, пройденного материальной
точкой за промежуток времени
,
если известна скорость
– это длина пути, пройденного материальной
точкой за промежуток времени
,
если известна скорость
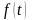 в момент времени
.
в момент времени
.
Экономический
смысл определенного интеграла:
определенный интеграл
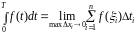 – это объем продукции, произведенной
за промежуток времени
– это объем продукции, произведенной
за промежуток времени
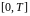 ,
если известна производительность труда
в момент времени
.
,
если известна производительность труда
в момент времени
.
