Лекция 3. Неопределенный интеграл

3.1. Интегрирование рациональных дробей

Рассмотрим интеграл .

Для вычисления этого интеграла сделаем такие преобразования: выделим полный квадрат из квадратного трехчлена и получим квадратный двучлен:

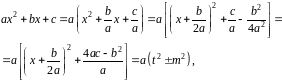
где В последнем равенстве берется знак плюс, если 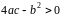, и знак минус, если .

Таким образом, интеграл будет иметь вид:

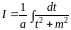, или .

Получили табличные интегралы.

Рассмотрим интеграл общего вида: .

В квадратном трехчлене выделим полный квадрат, проведем замену переменной и запишем данный интеграл в виде суммы двух интегралов:

где первый интеграл в правой части этого равенства равен модулю натурального логарифма знаменателя дроби, а второй – табличный.

Пример 1. Найти интеграл

Решение.

Из квадратного трехчлена выделим полный квадрат, получим:

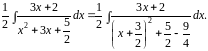
Сделаем замену переменной, положив

:

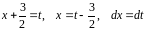3.2. Интегрирование выражений, содержащих квадратный трехчлен

Рассмотрим интегралы вида:

и .

И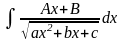нтегралы этого типа с помощью преобразований, а именно выделения полного квадрата в квадратном трехчлене и замены переменной приводятся к табличным интегралам.

Отметим, что квадратный трехчлен 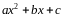при этом должен быть положительным .

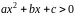Пример 2. Найти интеграл

Решение.

Рациональной функцией называется отношение двух многочленов: . Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, то есть когда , и неправильной – в противоположном случае, когда .

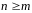Рациональную неправильную дробь всегда можно записать в виде:

,

где 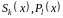– многочлены, причем степень многочлена меньше степени многочлена . Для этого нужно разделить числитель на знаменателя по правилу деления многочленов.

Следовательно, интегрирование неправильной рациональной дроби сводится к интегрированию целой части (многочлена) и правильной рациональной дроби.

Рассмотрим интегрирование элементарных дробей типа:

1) ;

2) ( – целое, );

3) 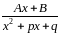( 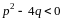, то есть квадратный трехчлен не имеет действительных корней).

Для вычисления интегралов 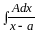и нужно сделать замену переменной 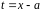, а .

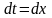Тогда:

.

.

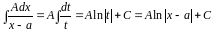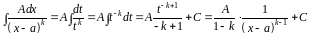Для вычисления интеграла 3) в знаменателе выделяем полный квадрат и делаем замену:

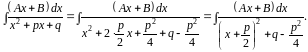
Замена .

Теперь: .

Последний интеграл запишем как сумму двух интегралов, а именно:

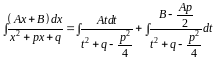, если

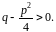
Возвращаемся к переменной :

3.3. Разложение дроби на простейшие

Рассмотрим общий подход к интегрированию правильной рациональной дроби , где .

Для этого нужно:

1. Разложить знаменатель 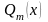на простые действительные множители. По основной теореме алгебры это разложение может иметь линейные и квадратичные множители:

,

при этом квадратичные трехчлены не имеют действительные корни.

2. Написать разложение данной рациональной дроби на элементарные (самые простые) дроби в таком виде:

где 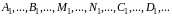– некоторые постоянные.

Нужно заметить, что в этом разложении будет столько дробей, сколько корней имеет многочлен , включая их кратность 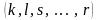. Знаменателями простых дробей являются все целые степени каждого множителя , начиная с первой степени и заканчивая той степенью, которая имеет множитель в разложении .

Числителями простых дробей будут или постоянные , или линейные функции , в зависимости от того, есть ли в знаменателе дроби какая-либо степень линейной или квадратичной функции.

3. Избавиться от знаменателя в последнем расписании, для чего нужно умножить обе части равенства на .

4. Составить и решить систему уравнений, сравнивая коэффициенты при одинаковых степенях в обеих частях полученного тождества. (Количество этих уравнений должно равняться количеству неизвестных ).

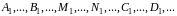Систему уравнений для нахождения неизвестных можно найти иначе. Учитывая, что тождество имеет место при любых значениях , присваиваем произвольные числовые значения. Как правило присваивают значения корней . Также можно комбинировать эти способы.

5. Решить полученную систему уравнений. Найденные значения подставить в разложение рациональной дроби.

Следовательно, интегрирование правильной рациональной дроби сводится к интегрированию элементарных дробей.

Примеры. Найти интегралы.

3.

Решение.

Приравняем знаменатель подынтегральной функции к нулю: откуда имеем корни .

Тогда подынтегральную дробь можно переписать так:

Это правильная рациональная дробь, которую можно разложить на простые дроби таким образом:

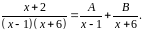
Приводя к общему знаменателю и приравнивая числители, получим:

.

Теперь найдем коэффициенты . Подставим в последнее равенство значения корней знаменателя, тогда:

.

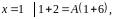
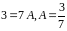Перепишем интеграл и с учетом предыдущих преобразований, найдем его:

.

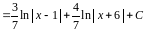4.

Решение.

Здесь, как видим, под знаком интеграла имеем неправильную рациональную дробь. Разделим числитель на знаменатель по правилу деления многочленов, тогда имеем: ,

откуда:

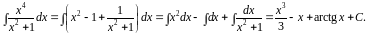
5.

Решение.

Под интегралом правильная рациональная дробь. Разложим эту дробь на простые:

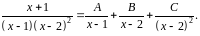
Приводя к общему знаменателю и приравнивая числители, имеем:

.

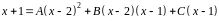Находим коэффициенты .

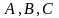Сначала в обе части подставляем корни знаменателя :

.

Осталось найти .

Его можно найти, если приравнять коэффициенты, например при в обеих частях:

.

Следовательно,

6. .

Решение.

Под знаком интеграла знаменатель правильной дроби имеет лишь один действительный корень , а уравнение не имеет действительных корней, тогда разложение на элементарные дроби будет иметь вид:

.

Приводим к общему знаменателю и приравниваем числители:

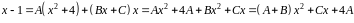
Определяем :

.

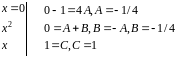Следовательно, интеграл запишется в виде суммы двух интегралов от простых дробей, которые легко интегрируются: