Лекция 1. Неопределенный интеграл
1.1. Понятие первообразной функции и неопределенного интеграла
Одной
из основных задач
дифференциального исчисления является
поиск производной данной функции.
Разнообразные исследования во многих
направлениях науки, в том числе
экономической, приводят к решению
обратной задачи, а именно по
данной
функции
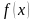найти такую функцию
,
производная которой равна функции
,
то есть
.
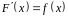Восстановление функции по известной производной этой функции составляет одну из основных задач интегрального исчисления.
Следовательно, если
,
то
.
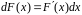Обозначим
,
тогда дифференциал функции:
.
(1.1)
Функция
называется первообразной
функцией для
функции
на множестве
,
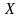если для любой переменной
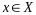функция
дифференцируема и
,
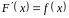или
.
Примеры. Найти первообразные для функций:
1.1.
Пусть функция
,
тогда
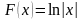– первообразная для функции
,
потому что
.
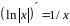1.2.
Если
на интервале
,
то
–
первообразная, потому что в любой точке
этого интервала
.
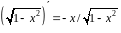1.3.
Если
,
то
,
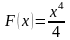потому что
.
При
этом также
,
потому что
.
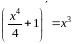Следовательно,
,
где
– произвольная постоянная.
В примерах, которые приведены выше, общий вид всех первообразных для заданных функций будет:
1.
.
2.
,
.
3.
,
.
Теорема.
1.
Если
– первообразная для
на
,
то
,
также первообразная для
,
где
– постоянная величина.
2.
Если
и
– две
первообразные для
на
,
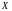то
,
то есть эти функции отличаются одна от
другой на постоянную величину.
Доказательство.
То, что вместе с функцией функция также является первообразной для функции , очевидно, так как
.
Для доказательства второй части теоремы составим функцию:
,
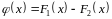где
и
,
поскольку эти функции первообразные
для
.
Тогда
,
.
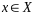Откуда,
функция
,
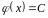то есть
.
Теорема доказана.
Из
данной теоремы вытекает, что если
– одна из первообразных для
,
то множество всех первообразных имеет
вид
.
Если функция – первообразная для функции , то множество функций , где – произвольная постоянная, называется неопределенным интегралом от функции и обозначается таким образом:
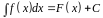, (1.2)
где
символ
–
интеграл, а
подынтегральное выражение,
– подынтегральная функция,
– переменная интегрирования.
Операция восстановления функции по ее производной, или нахождение функции , называется интегрированием .
Из
геометрического содержания производная
является угловым коэффициентом
касательной к кривой
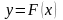в точке с абсциссой
.
Тогда найти первообразную для
значит найти такую кривую
,
что угловой коэффициент касательной к
ней в произвольной точке
был бы равен значению
в этой точке.
Из определения неопределенного интеграла можно сделать вывод: для того чтобы проверить правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла по независимой переменной равна подынтегральной функции, то есть:
. (1.3)
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, то есть:
а)
;
б)
.
3. Постоянный множитель можно выносить за знак интеграла:
.
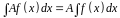4. Неопределенный интеграл от алгебраической суммы двух (или конечного числа) функций равен алгебраической сумме интегралов от этих функций:
.
(1.4)
5.
Если в подынтегральной функции переменную
интегрирования умножить на любой
постоянный множитель
,
то первообразная подынтегральной
функции делится на этот множитель:
, (1.5)
а также
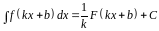. (1.6)
Все свойства доказываются дифференцированием правых частей приведенных равенств.