2. Математическая модель функционирования информационных систем

Нужно рассказать о всех известных вам способах описания функционирования технических систем(см вопрос 3). А потом описать систему с помощью теории систем массового обслуживания.

Системы массового обслуживания.

1. Одноканальные СМО

   • С отказами

   • С ожиданием

   • С ожиданием и неограниченной очередью

2. Многоканальные СМО

• С отказами

СМО характеризуются следующими параметрами:

- каналы обслуживания

- входной поток заявок

-правило обслуживания

-организация очереди

-организация обслуживания

Потоки заявок.

Простейшим потоком называется поток, обладающий следующими свойствами:

1.стационарность;

2.ординарность;

3.отсутствие последействия.

Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени длиной  зависит только от длины участка и не зависит от того, где именно на оси времени расположен этот участок.

Поток событий называется ординарным, если вероятность попадания на элементарный участок t двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Ординарность означает, что поток прореженный, т.е. между любыми двумя событиями есть временной интервал.

Поток событий называется потоком без последействия, если для любых, не перекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Это означает, что заявки попадают в систему не зависимо друг от друга.

Одноканальная СМО с отказами. -канал свободен и готов к обслуживанию, заявок в системе нет. -канал занят и в системе находится одна заявка.

Составим систему Колмогорова (правило составления: минус исходящая интенсивность, плюс входящая интенсивность):

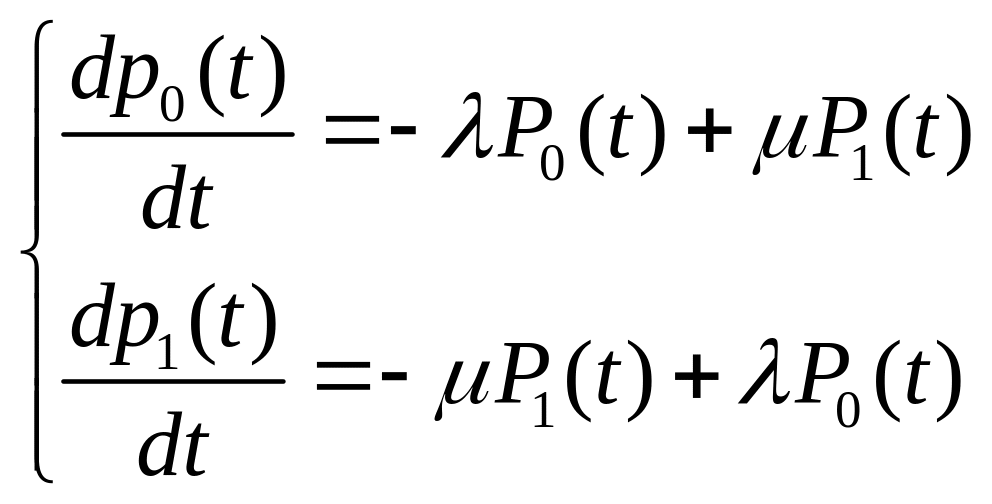Н.У.:

Решение системы будет следующим:

Ро-это вероятность обслуживания заявки

3.Способы описания надежности функционирования информационных систем.

1. Структурная схема системы.

Основное достоинство метода – это высокая наглядность.

Недостаток - неполная информация о структуре объекта.

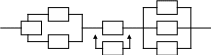
2. Описание функционирования системы с помощью алгебры-логики.

Пусть 0-элемент в отказе, 1-элемент исправен и работает.

Тогда функционирование системы можно описать с помощью ФАЛ, используя операции конъюнкции, дизъюнкции и инверсии.

Y(x₁x₂x₃x₄)=

	х1	х2	х3	х4	y
1	0	0	0	0	0
2	1	0	0	0	0
3	0	1	0	0	0
4	0	0	1	0	0
5	0	0	0	1	0
6	1	1	0	0	0
7	1	0	1	0	0
8	1	0	0	1	0
9	0	1	1	0	0
10	0	1	0	1	0
11	1	1	1	0	0
12	1	1	0	1	0
13	1	0	1	1	1
14	0	1	1	1	1
15	0	0	1	1	0
16	1	1	1	1	1

3. Матрица состояний системы.

В матрице состояний, каждая строка представляет собой вектор, компонентами которого служат признаки о том. в каком состоянии прибывает каждый элемент, когда сама система находится в состоянии i, i E, где Е-это множество всех состояний системы. Пусть n число состояний системы. Все состояния системы можно разбить на два подмножества: работоспособное состояние E₊ и множество отказовых состояний Е_-

В каждый момент времени t для К-го состояния определяют шесть подмножеств множества всех элементов.

Rk-подмножество всех исправных элементов системы

Wk-подмножество всех ремонтируемых элементов сиситемы

R’k- подмножество всех элементов находящихся в состоянии простоя, в следствии прерывания их функционирования

W’k- подмножество всех элементов, находящихся в состоянии простоя, в следствии прерывания их восстановления

W⁰k- подмножество всех элементов, находящихся в очереди на восстановление

R⁰k подмножество всех элементов, находящихся в очереди на работу.

С каждым состоянием свяжем вектор Ак=(а_1к,а_2к,…а_nк), характеризующий состояние всех элементов системы в момент времени t.

Si, если R’k v Rk

a_ik = τi, если W’k v Wk

0, если W⁰k v R⁰k

Таким образом, функционирование любой восстанавливаемой системы определяет матрица состояний S размером (mxn). Столбцами, которой служат векторы Ак.

4. Граф состояний системы.

Восстанавливаемая система, состоящая из n-элементов, может находиться во множестве различных состояний. Из-за постоянно возникающих отказов и восстановлений система в дискретный момент времени переходит из одного состояния в другое. Функционирование такой системы может быть описано графом, узлами которого являются состояния системы, а ветвям соответствуют различные переходы из состояния в состояние.

В ид графа зависит от структурной схемы системы, числа обслуживающих бригад и дисциплины обслуживания. Исправен - обозначаем кругом, отказ-прямоугольник.

Граф состояний дублируемой системы.

1 Система обслуживается 1 бригадой с прямым приоритетом

2 Систему обслуживает 2 бригады с прямым приоритетом

λ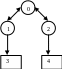 1μ1 λ2μ2 λ1μ1 λ2μ2

λ1 λ2 λ1 λ2

5. Формализованный способ построения графов состояния системы

Каждому узлу графа соответствует определенное состояние системы, совокупность состояний, когда в системе отказало i- устройств называется i-ым уровнем графа. Исходными данными для построения графа является структурное схема системы. Интенсивности отказов и восстановления, дисциплина обслуживания и вид восстановления. Суть метода:

проводятся горизонтальные линии, которым присваиваются номера 0, 1, 2..m.

Далее строится граф с λ-переходами от верхних уровней к нижним. На нулевом уровне отмечается точкой или кружком, состояние системы соответствующее исправному состоянию всех устройств.

Затем, на линии с номером 1, обозначаются узлы соответствующие первому уровню графа, число узлов первого уровня равно числу устройств структурной схемы. Соединяем нулевой узел со всеми узлами первого уровня и отмечая стрелками переходы. Получим неполный граф, который называется графом первого уровня с λ-переходами. Все элементы первого уровня нумеруются в соответствии с номерами в структурной схеме, а у ветвей записываются соответствующие им интенсивности. Все узлы соответствующие отказовым состояниям отмечаются перечеркнутыми кружками, из этих узлов λ-переходы на более высокие уровни отсутствуют. Для построения графа состояний 2-го уровня с λ-переходами на линии с номером 2 наносятся узлы графа соответствующие всем возможным состояниям системы, когда отказали 2 устройства. Узлы нумеруются 2-х разрядными числами, номера отказавших элементов структурной схемы и последовательности их отказов. соединяем ветвями соответствующие узлы 1-го и 2-го уровня и отмечаем стрелками соответствующие переходы, получим граф состояний системы 2-го уровня с λ-переходами и т.д.

4. Методы анализа надежности технических систем. Логико-вероятностные методы анализа надежности. (:Вы должны рассказать как из структурной схемы получить таблицу истинности и затем составить функцию для описания работоспособного состояния системы. После этого, заменить операции дизъюнкции и конъюнкции на алгебраические операции сложения и умножения соответственно, а логические переменные - на соответствующие вероятности состояния элементов, в итоге получим вероятность безотказной работы системы..)

Описание функционирования системы с помощью алгебры-логики.

Пусть 0-элемент в отказе, 1-элемент исправен и работает.

Тогда функционирование системы можно описать с помощью ФАЛ, используя операции конъюнкции, дизъюнкции и инверсии. Вероятности работоспособного состояния элементов: -соответственно. Вероятность отказа для первого и второго элементов -соответственно. Здесь в формулу (1) необходимо подставить вероятности и записать в алгебраическом виде(2,3).

(1)

	х1	х2	х3	х4	y
1	0	0	0	0	0
2	1	0	0	0	0
3	0	1	0	0	0
4	0	0	1	0	0
5	0	0	0	1	0
6	1	1	0	0	0
7	1	0	1	0	0
8	1	0	0	1	0
9	0	1	1	0	0
10	0	1	0	1	0
11	1	1	1	0	0
12	1	1	0	1	0
13	1	0	1	1	1
14	0	1	1	1	1
15	0	0	1	1	0
16	1	1	1	1	1

(2)

(3)

Методы анализа надежности. Методы, основанные на теории Марковских процессов

Случайный процесс Х(t) называется Марковским процессом или процессом без последействия (без памяти), если для любых двух моментов времени t₀ и t1 (t₀<t₁) распределение вероятности Х(t), при условии, что заданы все значения Х(t) (t≤t₀), зависит только от Х(t₀).

Для Марковского процесса зависимыми являются только два соседних состояния. Пусть t₀ –настоящее время, τ-прошедшее время и t₁ – будущее, то можно сказать, что для Марковских процессов прошедшее состояние никак не влияет на будущее. Марковский процесс называется однородным, если для двух любых возможных значений i и k, и τ≥0, вероятность события

Х(t+τ) =k, при условии, что Х(t)=i. Условная вероятность p_ik(τ)=P(X(t+τ))k при Х(t)=i)

Эта вероятность называется вероятностью перехода из состояния i в состояние j за единицу времени τ.

Для любых состояний i и j вероятности переходов обладают следующими свойствами:

1. P_ik(τ)≥0

2. Σp_ik(t)=1

3. p_ik(τ₁+ τ₂)= Σp_ik(τ₁) p_ik(τ₂)

Основным допущением метода, основанного на теории Марковских процессов, является:

1. Время отказа и время восстановления каждого элемента, входящего в систему имеют экспоненциальное распределение.

2. Функционирование системы контролируется непрерывно.

3. Восстановление элемента начинается сразу после его отказа, при наличии свободной бригады, обслуживающей данный элемент, при отсутствии ремонтной бригады, отказавший элемент становится в очередь на обслуживание.

Метод позволяет рассчитать надежность невосстанавливаемой и восстанавливаемой не резервируемой и структурно резервируемой технической систем.

Метод позволяет вычислить вероятность безотказной работы, среднее время безотказной работы,

Функцию и коэффициента готовности, наработку на отказ и среднее время восстановления.

Инженерная методика расчета надежности технических систем, на основе Марковских цепей, состоит из следующих этапов:

1. Формулировка понятия отказов и представления исходных данных.

2. Построения графа состояния, где Е₊ -исправные состояния и Е- -неисправные состояния.

3. Составление по графу системы дифференциальных уравнений (Колмагорова) для стационарного или нестационарного режима

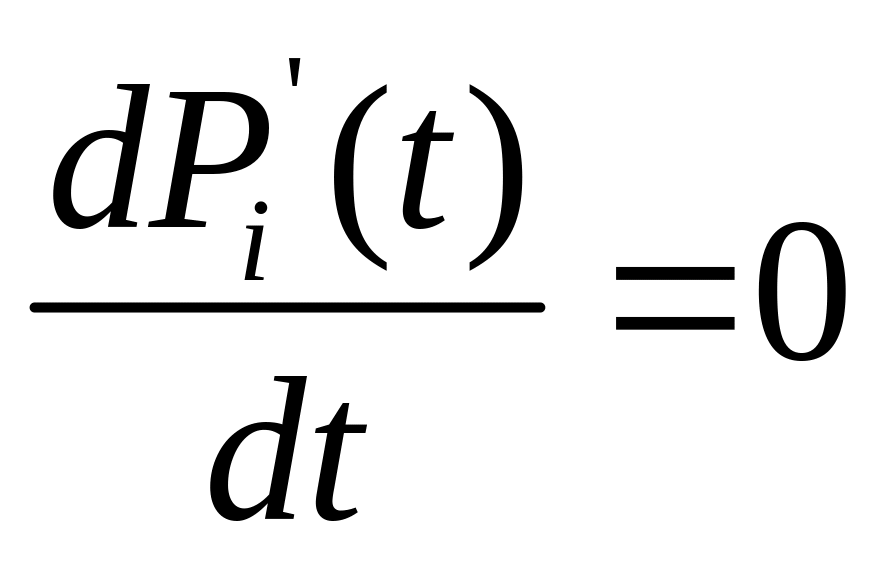
Вероятности состояний Pi(t) определяются путем решения системы диф. ур-й Колмагорова:

Удобнее всего решать с помощью преобразований Лапласа. Для этого в системе(1) вместо Pi(t) необходимо записать их изображение ,

В соответствии с этой заменой система диф.ур-ий будет выглядеть:

Эта система позволяет определить следующие показатели надежности:

1. Система работает до 1-го отказа, в этом случае вероятность безотказной работы системы за время t будет вычисляться по формуле:

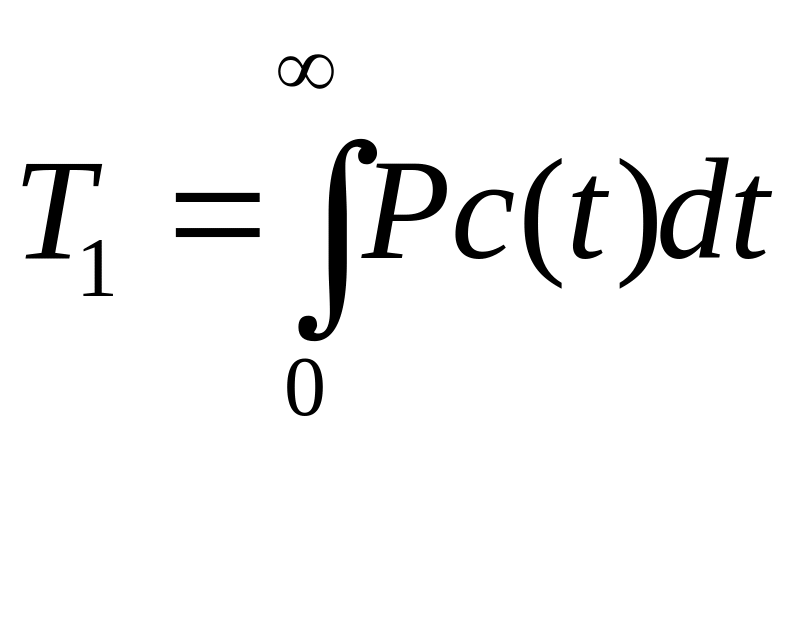
2. Система восстанавливается после наступления отказа.

После решения системы линейных уравнений, определяется стационарное значение вероятностей, которые равны

А по ним средняя наработка на отказ

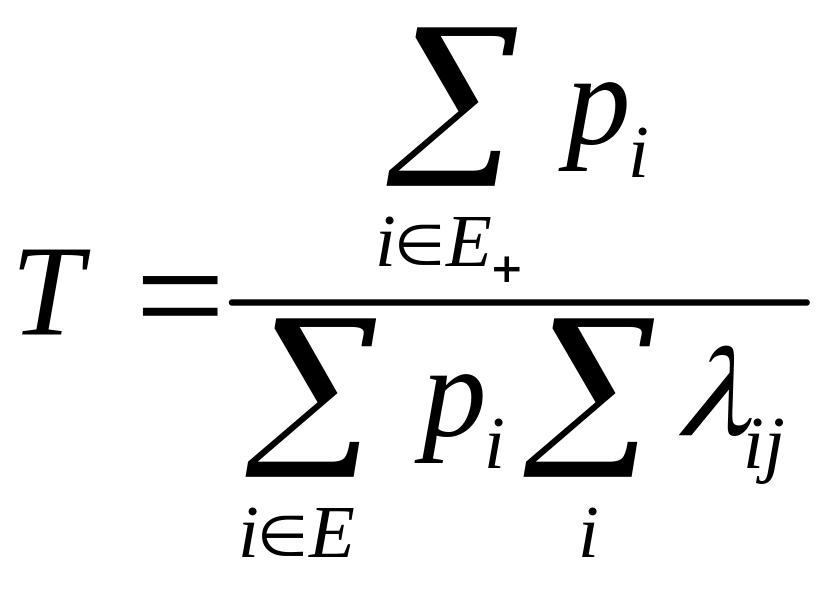
время восстановления

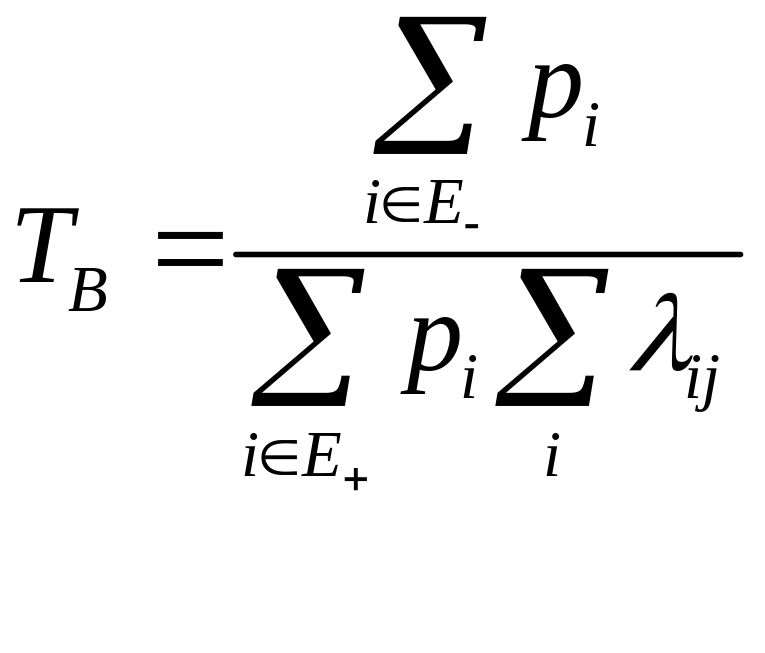
коэффициент готовности