6. Операции манипулирования данными в гиперкубе. Агрегация данных в гиперкубе.

Агрегация данных - суть получение значений, соответствующих меткам некоторого уровня иерархического измерения D на основе значений уровня .

Рассмотрим иерархическое измерение D с L уровнями (Рис. 2). Первичные данные (факты) соответствуют нижнему уровню иерархии ( ).

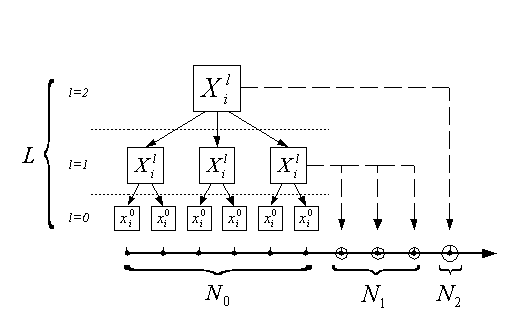
Рис. 2. Агрегация гиперкуба данных. Одномерное представление.

Вычисление агрегатов производится в соответствии с применяемым методом агрегирования. Например, в случае суммирования значение агрегата на уровне иерархии может быть вычислено по формул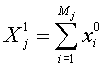е: , где - количество фактов, соответствующих меткам, являющимся дочерними по отношению к метке j.

Обобщая, получим формулы вычисления агрегатов по методу суммирования на остальных уровнях иерархии: ,

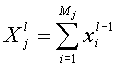Ось измерения D, первоначально содержащая метки, соответствующие нижнему уровню иерархии ( ), может быть дополнена метками, соответствующими уровням иерархии, начиная с . Таким образом, различие между метками, соответствующими первичным данным и метками, соответствующим агрегатам является условным.

Операция свертки данных в этом случае представляет собой построение среза гиперкуба данных, соответствующего смене метки уровня агрегации на уровень . Операция детализации соответствует смене метки уровня на уровень .

Количество агрегатов для одного измерения 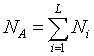. Рассмотрим случай двух измерений (Рис. 3).

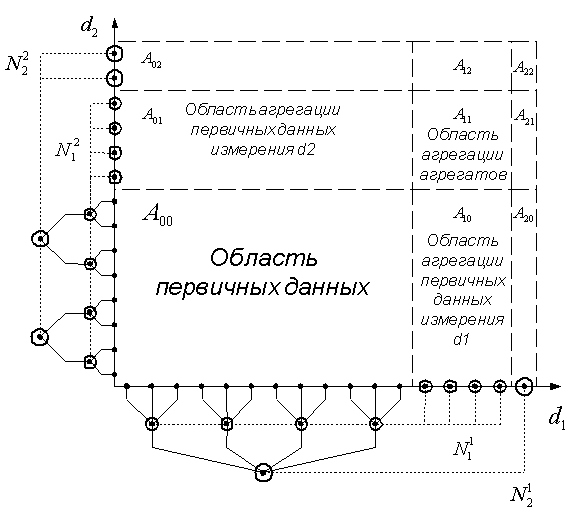
Рис. 3. Агрегация гиперкуба данных. Двумерное представление.

Количество агрегатов, хранимое в гиперкубе данных наряду с первичными данными, зависит от количества меток, соответствующих уровням иерархии измерений гиперкуба, начиная с , и может существенно превышать количество первичных данных.

В случае двух измерений число агрегатов будет составлять сумма значений областей: . С другой стороны, количество агрегатов может быть вычислено как разность количества всех значений гиперкуба и количества значений, соответствующих области первичных данных . Количество значений последней есть произведение . Таким образом, количество агрегатов гиперкуба данных в двумерном случае составляет:

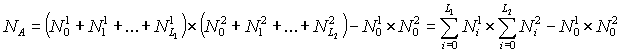
Обобщая на случай произвольного числа измерений D, получим: 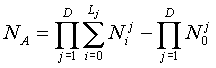, где - кол-во меток i-го уровня иерархии измерения , а - кол-во уровней иерархии измерения j.

7. Разреженный гиперкуб данных. Бинарное представление гиперкуба данных. Выборка данных из гиперкуба.

Наполнение гиперкуба данными при недостаточном количестве исходных данных приводит к образованию пустых ячеек. Гиперкубы данных с большим количеством пустых ячеек называют разреженными.

Введем оператор подсчета количества непустых ячеек , ставящий в соответствие множествам фиксированных измерений и фиксированных меток гиперкуба данных некоторое число , равное количеству непустых ячеек в области гиперкуба данных, соответствующей фиксированным значениям.

Количество всех ячеек , соответствующих множествам и будет равно произведению мощностей множеств по незафиксированным измерениям : . Тогда степень разреженности области гиперкуба данных (в процентах) на множествах фиксированных измерений и меток можно вычислить как отношение: ,

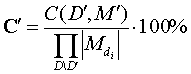Заметим, что при оператор принимает значение 0, если ячейка, соответствующая множеству пуста и 1 в противном случае. Степень разреженности гиперкуба в целом: ,

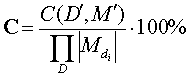Оценка заполненности многомерной базы данных может быть произведена на основе анализа хранилища данных до начала операции формирования гиперкубов данных. Вычисление значений оператора на различных наборах и позволяет оценить степень заполнения хранилища данных и построить гиперкуб данных заданной плотности путем отбрасывания меток, соответствующих пустым ячейкам.

Введение оператора является основой формального подхода к описанию плотности гиперкубов данных и решению множества задач, связанных с оценкой заполненности многомерных баз данных. Некоторые из этих задач будут рассмотрены далее подробно.

Бинарное представление

Для вычисления значения оператора может быть использована модель бинарного представления гиперкуба данных (Рис. 4).

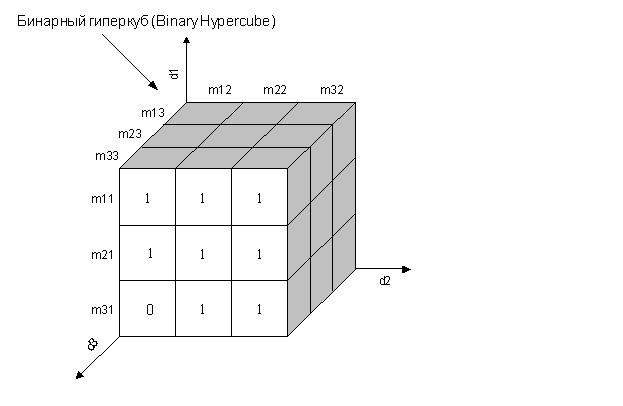
Рис. 4. Бинарное представление гиперкуба данных

Бинарное представление гиперкуба данных представляет собой гиперкуб , структура которого в точности повторяет структуру гиперкуба данных . Однако вместо значений, содержащихся в ячейках гиперкуба данных , ячейки бинарного гиперкуба содержат: 1 - если соответствующая ячейка содержит числовое значение, 0 - если соответствующая ячейка пуста.

Таким образом, гиперкуб является бинарным представлением гиперкуба данных , характеризующим степень его заполненности.

Значение оператора может быть вычислено как сумма значений бинарного гиперкуба : ,

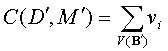где - срез бинарного гиперкуба, соответствующий множествам фиксированных значений , гиперкуба данных .

Множество значений операторов, соответствующих выбранному измерению , может быть определено как одномерная проекция бинарного представления гиперкуба данных по выбранному измерению .

Аналогично определяется двумерная проекция по выбранным измерениям и трехмерная проекция. Построение одно-, двух- и трехмерных проекций бинарного представления гиперкуба данных является основой создания карт заполненности многомерных баз данных и может быть использовано при решении различных задач, связанных с обработкой данных в многомерных базах данных с неполной информацией.