Матричная форма системы нормальных уравнений. Информационная матрица.
qiu – i независимый параметр номера точки плана u. qlu – l параметр точки плана u. l=0,1,2,…L; u=1,2,…N; i=1,2,…n.
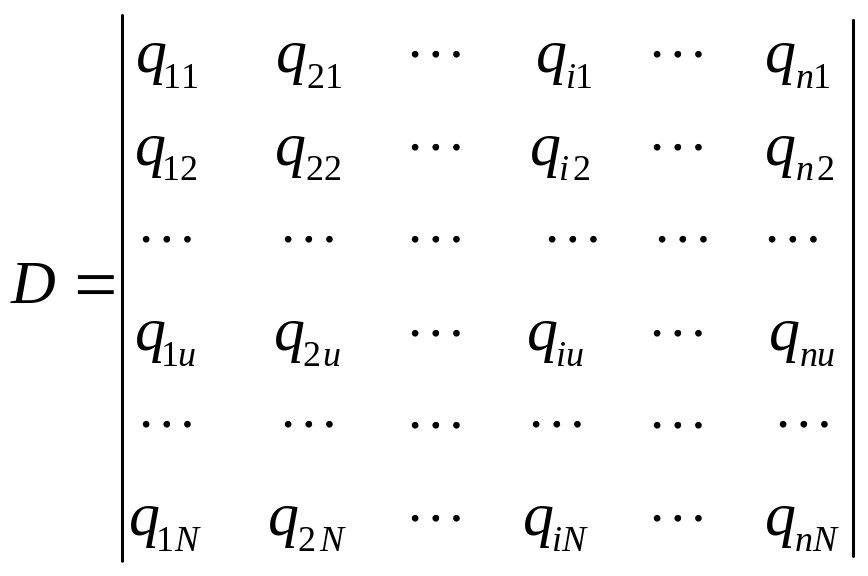- матрица планирования эксперимента
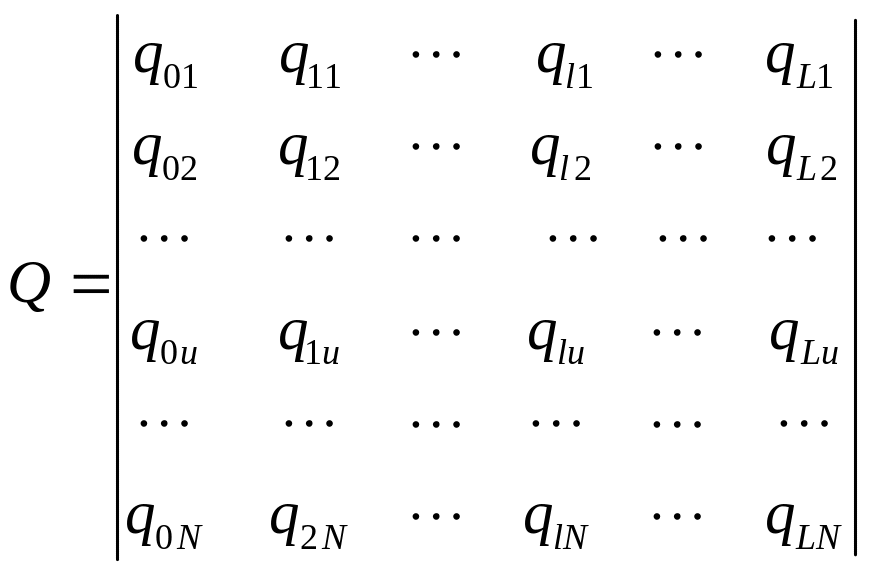
- транспонированная матрица является
основной.
M – информационная матрица
(матрица моментов).
- (L+1) строк; N
- столбцов.
Q – N*(L+1); M - (L+1)*(L+1)
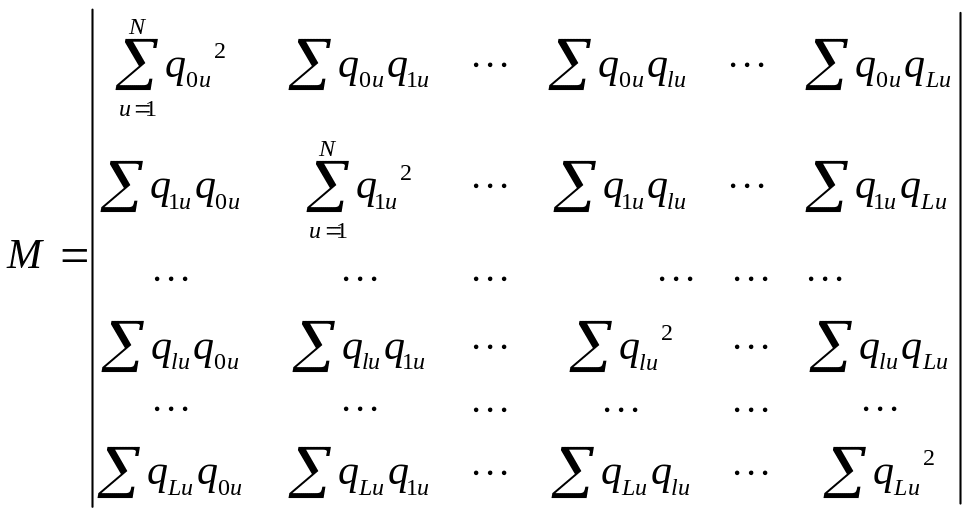
Рассмотрим 2 вектора. B – вектор искомых коэффициентов; K – вектор значения показателей.
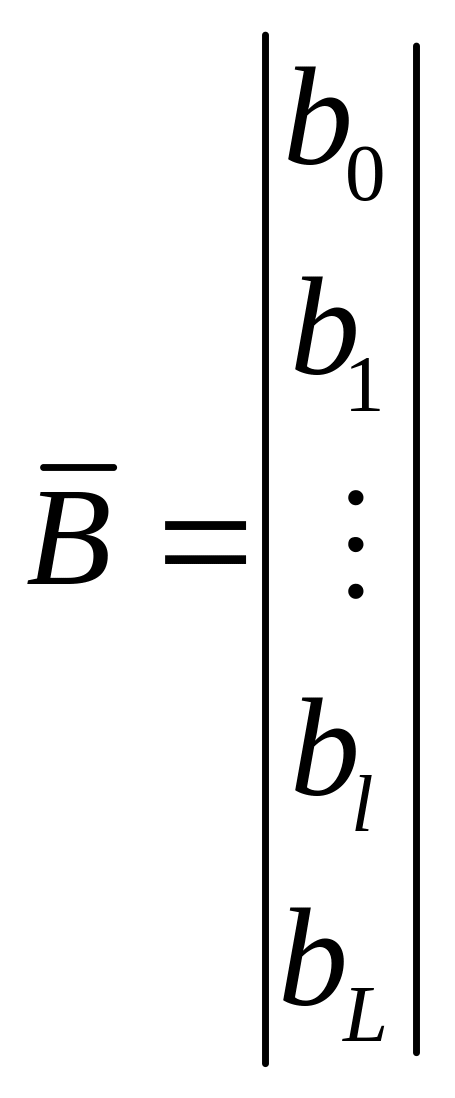
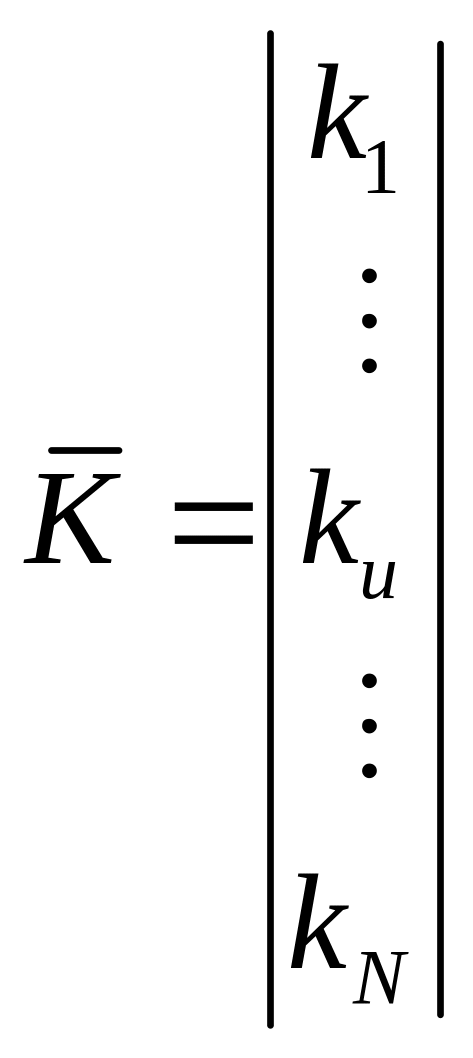
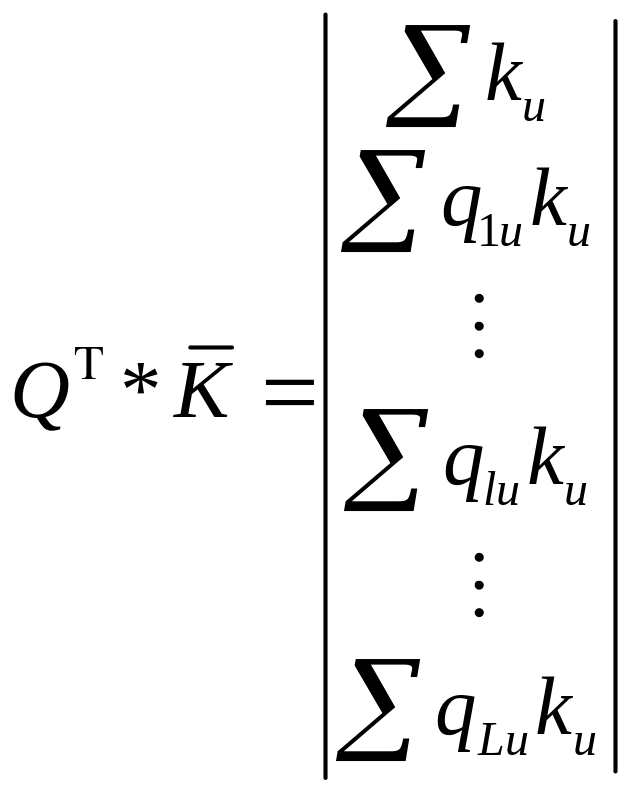
- по аналогии с системой нормальных
уравнений (система нормальных уравнений
в матричной форме).
Умножим левую и правую часть слева на
.
;
- единичная матрица.
- универсальное решение в матричной
форме.
Свойства матрицы M:
Квадратная симметричная матрица;
В главной диагонали – сумма квадратов элементов;
Недиагональные элементы симметричны и равны;
Если матрица наблюдения ортогональна, то она хорошо обращается;
Матрица, обратная матрице M,
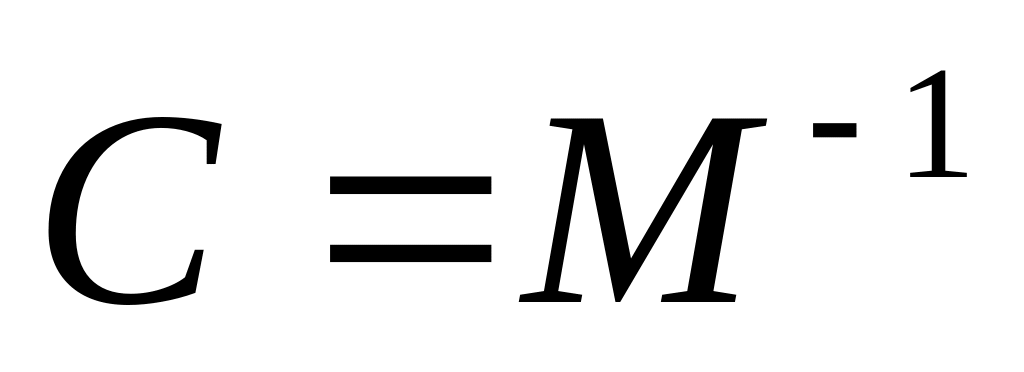- ковариационная. Она определяет свойства
плана.
Исследование судовых систем на основе полного факторного эксперимента.
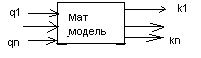Задача найти
k(q1,q2,…qn).
qi соответствует Si уровень. При ПФЭ рассчитывается сочетание всех уровней параметров.
- количество всех сочетаний (опытов).
Если
,
то
.
Обычно рассматривается случай когда
Si=2. 1 уровень - qimin;
2 уровень - qimax.
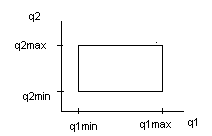ПФЭ соответствует
координатам вершин (точки плана
эксперимента).
Пронормируем все параметры:
Центрирование
Нормирование
qi0
– среднее значение.
- половина диапазона.
- нормированное значение.
Типовые планы не зависят от принципов размерности, если переходим к нормированным единицам.
- третья сумма обычно не используется.
ПФЭ в математическом виде: D – план эксперимента.
- для одного фактора
Выразим Dr+1 через Dr
,
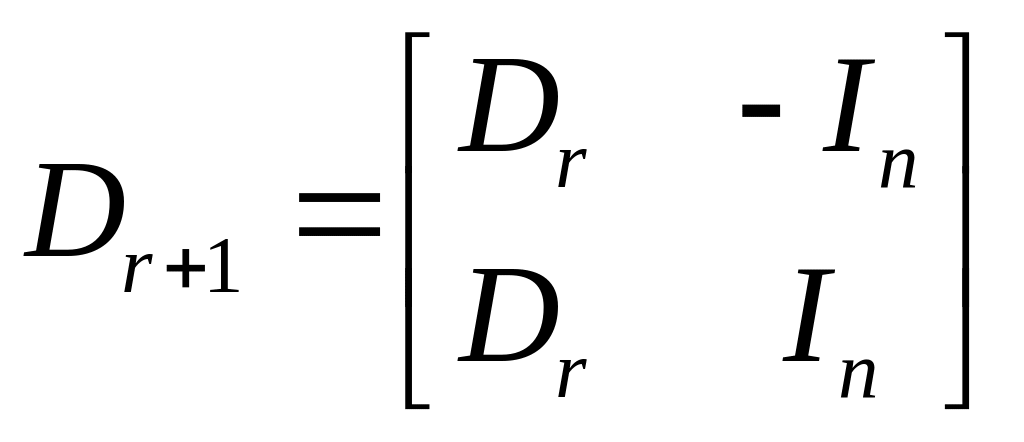где
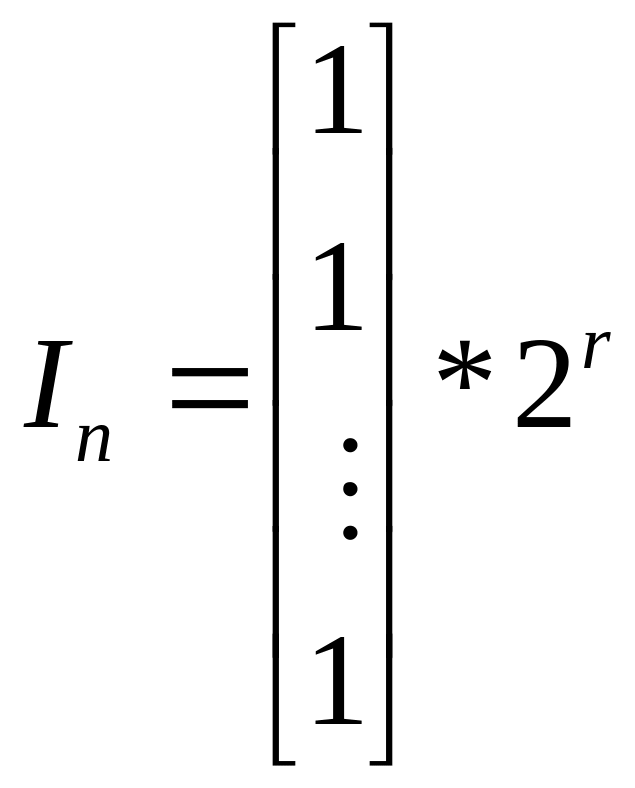
Недостаток матрицы планирования D. Она не учитывает, какую модель мы хотим получить. Для того чтобы получить вводиться понятие матрицы наблюдения.
Для N=3
Q=
1 |
q1 |
q2 |
q3 |
q1q2 |
q1q3 |
q2q3 |
1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
qiu – нормированные параметры в u-том эксперименте u=1,2,…N
qlu – зависимые переменные l=0,1,2,…L.
Рассмотрим свойства матрицы наблюдения:
Симметрия кроме 1го столбца
Свойство нормировки. Если все возвести в квадрат и сложить получится N.
Свойство ортогональности.
Если большой диапазон изменения параметров, то модель получается неадекватная, потому что все зависимости нелинейные. ПФЭ может применяться только в небольшом диапазоне изменений. ПФЭ в большинстве случаев является частью какого-то более сложного плана.