8. Синусоидальный ток в емкости.

Д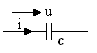 ано: , С

Найти:

Реактивное сопротивление емкости, измеряется в (Ом): .

1) => - закон Ома для действ-их значений U и I в емкости.

2) => в емкости ток опережает напряжение на 90⁰.

, .

0<t</2 емкость накапливает энергию магн. поля, /2<t<накопленная энергия возвращается в источник.

Актив. мощность в индуктивности P=0 (площадь «+» полуволны компенс. площ. «-» полуволны).

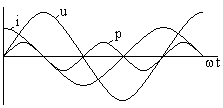
9. Синусоидальный ток в индуктивности.

Дано: , L

Найти:

, .

Индуктивное сопротивление, измеряется в (Ом): .

1) => - закон Ома для действ-их значений U и I в индуктивности.

2) => в индуктивности напряжение опережает ток на 90⁰.

, .

0<t</2 индуктивность накапливает энергию магн. поля, /2<t<накопленная энергия возвращается в источник.

Актив. мощность в индуктивности P=0 (площадь «+» полуволны компенс. площ. «-» полуволны).

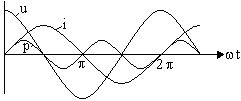
10. Полное сопротивление и комплексное сопротивление двухполюсника.

Входное сопротивление двухполюсника . В общем случае .

П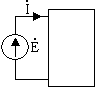 ри входное сопротивление имеет индуктивный характер , при - емкостный и при - чисто активный.

- входное реактивное сопротивление.

- полное сопротивление

- комплексное сопротивление.

11. Законы Ома и Кирхгофа в комплексной форме.

Д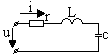 ано: r, L, c,

Найти: - ?

(1)

Обозначим: - комплексное сопротивление сопротивления;

- комплексное сопротивление индуктивности;

- комплексное сопротивление ёмкости.

Тогда: (5) – комплексная амплитуда напряжения на сопротивлении.

(6) - комплексная амплитуда напряжения на индуктивности.

(7) – комплексная амплитуда напряжения на ёмкости.

Выражения (5), (6), (7), - закон Ома в комплексной форме записи для отдельных элементов цепи.

С учетом введенных обозначений:

- II закон Кирхгофа в комплексной форме записи.

Из (4)→

- реактивное сопротивление цепи

- входное комплексное сопротивление цепи.

- полное сопротивление цепи

- угол сдвига фаз между током и напряжением

(9) – закон Ома в комплексной форме для всей цепи.

;

После определения комплексной амплитуды тока осуществляем переход к мгновенному значению: .

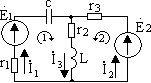
Закон Ома в комплексной форме записи:

Второй закон Кирхгофа в комплексной форме записи:

1)

2)

Где комплексные действующие значения:

Закон Ома:

Первый закон Кирхгофа: .

Второй закон Кирхгофа:

12. Векторная диаграмма.

Векторной диаграммой называется совокупность векторов на комплексной плоскости, отображающих синусоидально изменяющие функции времени одинаковой частоты, и построенных с соблюдением их взаимной ориентации по фазе.

Векторная диаграмма позволяет производить сложение и вычитание синусоидальных функций времени.

Д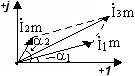 ано: ,

Найти:

Геометрическая сумма векторов дает комплексную амплитуду искомого третьего тока.

Длина вектора равна амплитуде тока, а угол между действительной осью и самим вектором равен начальной фазе искомого тока.

Векторные диаграммы дают наглядное представление о фазных соотношениях между токами и напряжениями отдельных элементов (участков цепи).

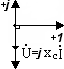
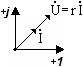
1 .Сопротивление: 3.Ёмкость:

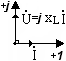
2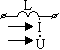 .Индуктивность:

Частный случай векторной диаграммы – топографическая векторная диаграмма на которой вектора располагаются последовательно друг за другом, а порядок их расположения соответствует порядку расположения элементов в цепи.