1. Определение тока, потенциала, напряжения.

Ток – упорядоченное движение свободных носителей электрических зарядов.

Сила тока определяется как предел отношения количества электричества проходящего через поперечное сечение проводника за интервал времени Δt, при условии стремления последнего к нулю.

Маленькая буква i обозначает мгновенное значение величины .

Если через поперечное сечение проводника за равные промежутки времени переносятся одинаковые по величине и знаку заряды, то такой ток называется постоянным:

Потенциал данной точки поля – величина, равная работе электростатической силы по перемещению единичного заряда из данной точки поля 1 в бесконечно удаленную точку: . Или

Потенциал в данной точке поля равен потенциальной энергии, которой обладает единичный положительный заряд, помещенный в эту точку поля:

Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка:

2. Источники эдс и тока.

При расчётах электрических цепей пользуются идеализированными источниками электрической энергии – источниками Э. Д.С. и тока. Им приписываются следующие свойства:

Идеальный источник ЭДС –активный элемент с 2мя выводами, напряжение на кот. не зависит от величины тока протекающего ч/з источник. Внутреннее сопротивление идеал. ЭДС = 0.

Величина численно равная работе, совершаемой сторонними силами, при перемещении единичного «+» заряда от клеммы « - » к клемме «+» называется ЭДС источника и обозначается Е. Стрелка внутри ЭДС указывает на направление возрастания потенциала.

Идеал. источ. ЭДС является источником с бесконеч. мощностью. Реал. источ. ЭДС конечной мощности, изображается виде послед. включенных идеал. источ. ЭДС и сопротивления, кот. ограничивает мощность отдаваемую во внеш. цепь.

Источник тока представляет собой идеализированный источник питания, который создает ток , не зависящей от сопротивления нагрузки, к которой он присоединен, а его ЭДС и внутреннее сопротивление равны бесконечности.

3. Закон Ома для участка цепи с эдс.

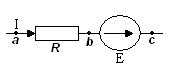
Закон Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φа-φс) на концах участка цепи и имеющейся на этом участке ЭДС.

Так, для схемы рис.1.а: Так, для схемы рис.1.б:

, ,

рис.1.а рис.1б

В общем случае: (1.1а)

Уравнение (1.1а) математически выражает закон Ома для участка цепи, содержащего источник ЭДС; знак плюс перед E соответствует рис.1.а, знак минус – рис.1.б. В частном случае при E=0 уравнение (1.1а) переходит в уравнение (1.1) (1.1)