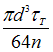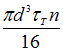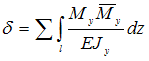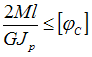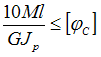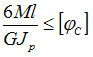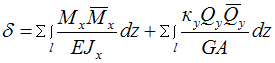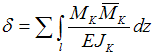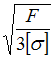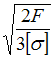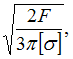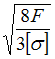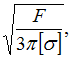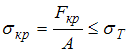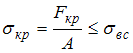Задание n 6
Тема:
Крутящий момент. Деформации и
напряжения
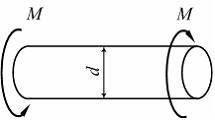 На
рисунке показан стержень, работающий
на кручение. Известны величины:
На
рисунке показан стержень, работающий
на кручение. Известны величины: ![]() –
предел текучести при чистом сдвиге, n –
коэффициент запаса по текучести в самых
напряженных точках. Значение М равно …
–
предел текучести при чистом сдвиге, n –
коэффициент запаса по текучести в самых
напряженных точках. Значение М равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Коэффициент
запаса по текучести в самых напряженных
точках определяется по формуле  где
где  После
подстановки получаем
После
подстановки получаем 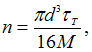 откуда
откуда 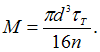
ЗАДАНИЕ
N 7
Тема:
Расчет на жесткость при кручении
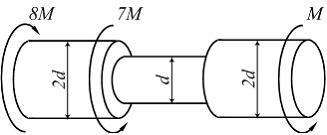 Максимальный
относительный угол закручивания для
стержня, показанного на рисунке, равен …
Известны величины: М, d, G –
модуль сдвига материала стержня.
Максимальный
относительный угол закручивания для
стержня, показанного на рисунке, равен …
Известны величины: М, d, G –
модуль сдвига материала стержня.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Стержень
имеет три участка (левый, средний и
правый). Относительный угол закручивания
определим по формуле  где
где ![]() и
и 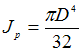 –
крутящий момент и полярный момент
инерции поперечного сечения на
соответствующем участке. После вычислений
получаем:
–
крутящий момент и полярный момент
инерции поперечного сечения на
соответствующем участке. После вычислений
получаем:
![]()
![]()
![]() таким
образом
таким
образом ![]()
ЗАДАНИЕ N 8 Тема: Чистый сдвиг. Расчет на сдвиг (срез) Напряженное состояние «чистый сдвиг» имеет место при нагружении тонкостенной трубки по схеме, показанной на рисунке …
|
|
|
2 |
|
|
|
1 |
|
|
|
4 |
|
|
|
3 |
Решение: Двумя поперечными и двумя продольно-осевыми сечениями выделим элемент стенки трубки (см. рис.). Известно, что в поперечном сечении трубки при кручении действуют касательные напряжения. По закону парности такие же напряжения действуют в продольно-осевых сечениях. Нормальные напряжения в этих сечениях равны нулю. Поэтому напряженное состояние стенки трубки – «чистый сдвиг».
ЗАДАНИЕ
N 9
Тема:
Статическая неопределимость. Степень
статической неопределенности
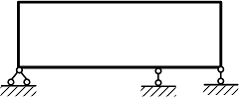 Число
дополнительных связей наложенных на
раму равно …
Число
дополнительных связей наложенных на
раму равно …
|
|
|
четырем |
|
|
|
трем |
|
|
|
одному |
|
|
|
двум |
ЗАДАНИЕ
N 10
Тема:
Расчет простейших статически неопределимых
систем
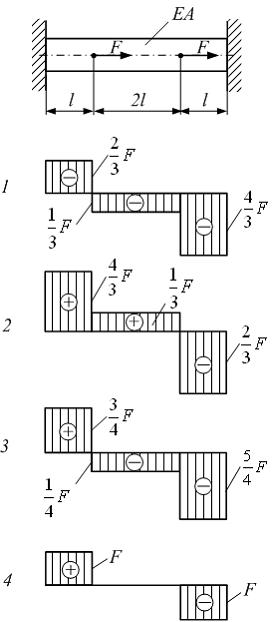 Стержень
нагружен внешними силами F.
Модуль упругости материала Е,
площадь поперечного сечения А,
размер l заданы.
Эпюра продольных сил показана на
рисунке …
Стержень
нагружен внешними силами F.
Модуль упругости материала Е,
площадь поперечного сечения А,
размер l заданы.
Эпюра продольных сил показана на
рисунке …
|
|
|
4 |
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
Решение:
В
геометрическом отношении стержень
симметричен относительно плоскости
симметрии I–I.
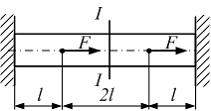 Внешняя
нагрузка относительно плоскости
симметрии расположена кососимметрично.
В
симметричной системе в плоскости
симметрии при кососимметричной нагрузке
симметричные силовые факторы равны
нулю. Продольная сила – симметричный
силовой фактор. Следовательно, на среднем
участке продольная сила равна нулю.
Эпюра продольных сил, при данном варианте
нагружения стержня показана на рисунке
4.
Внешняя
нагрузка относительно плоскости
симметрии расположена кососимметрично.
В
симметричной системе в плоскости
симметрии при кососимметричной нагрузке
симметричные силовые факторы равны
нулю. Продольная сила – симметричный
силовой фактор. Следовательно, на среднем
участке продольная сила равна нулю.
Эпюра продольных сил, при данном варианте
нагружения стержня показана на рисунке
4.
ЗАДАНИЕ
N 11
Тема:
Метод сил
Система
канонических уравнений для системы два
раза статически неопределимой, имеет
вид
![]()
![]() Коэффициент,
который определяет перемещение по
направлению неизвестной силы
Коэффициент,
который определяет перемещение по
направлению неизвестной силы ![]() от
единичного фактора
от
единичного фактора ![]() ,
обозначен …
,
обозначен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Система
канонических уравнений для раскрытия
статической неопределимости системы
методом сил имеет вид
Коэффициент ![]() –
это есть перемещение по направлению i-го
силового фактора под действием единичного
фактора, заменяющего j-й
фактор.
Следовательно,
–
это перемещение в направлении неизвестной
силы
от
единичной силы
–
это есть перемещение по направлению i-го
силового фактора под действием единичного
фактора, заменяющего j-й
фактор.
Следовательно,
–
это перемещение в направлении неизвестной
силы
от
единичной силы ![]() .
.
ЗАДАНИЕ
N 12
Тема:
Определение перемещений с помощью
интегралов Мора. Правило Верещагина
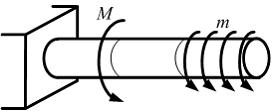 Для
данной расчетной схемы формула интеграла
Мора имеет вид …
Для
данной расчетной схемы формула интеграла
Мора имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
В
данной схеме все грузовые участки
стержня работают на кручение. Единственным
отличным от нуля внутренним силовым
фактором является крутящий момент.
Следовательно, формула интеграла Мора
для данной расчетной схемы имеет вид

ЗАДАНИЕ
N 13
Тема:
Формула Эйлера для критической силы
сжатого стержня и пределы ее
применимости
Стержень
изготовлен из малоуглеродистой стали
(предел пропорциональности ![]() модуль
упругости
модуль
упругости ![]() ).
Гибкость стержня
).
Гибкость стержня ![]() Для
определения критической силы сжатого
стержня необходимо использовать …
Для
определения критической силы сжатого
стержня необходимо использовать …
|
|
|
формулу Эйлера |
|
|
|
формулу Ясинского |
|
|
|
закон Гука при сжатии |
|
|
|
формулу Энгессера |
ЗАДАНИЕ
N 14
Тема:
Влияние условий закрепления концов
стержня на величину критической
силы
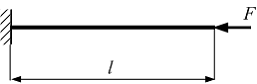 Стержень
длиной l сжимается
силой F.
Схема закрепления показана на рисунке.
Приведенная длина стержня равна …
Стержень
длиной l сжимается
силой F.
Схема закрепления показана на рисунке.
Приведенная длина стержня равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Приведенная
длина стержня определяется по
формуле ![]() где
− коэффициент
приведения длины, который учитывает
условия опирания стержня. Для стержня
с одним защемленным, а другим свободным
концами
где
− коэффициент
приведения длины, который учитывает
условия опирания стержня. Для стержня
с одним защемленным, а другим свободным
концами ![]() Тогда
Тогда ![]()
ЗАДАНИЕ N 15 Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость Стержень длиной сжат силой F. Схема закрепления показана на рисунке а. Зависимость критического напряжения от гибкости для материала Ст. 3 приведена на рисунке б. Поперечное сечение швеллер №10. Площадь поперечного сечения радиусы инерции Значение критической силы равно ____ кН.
|
|
|
247 |
|
|
|
124 |
|
|
|
318 |
|
|
|
212 |
Решение:
Определим
гибкость стержня по формуле
 При
данных условиях закрепления коэффициент
приведения длины
Тогда
При
данных условиях закрепления коэффициент
приведения длины
Тогда 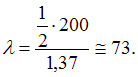 Из
графика зависимости критического
напряжения от гибкости видно, что при
определении критического напряжения
необходимо использовать формулу
Тетмайера-Ясинского
Из
графика зависимости критического
напряжения от гибкости видно, что при
определении критического напряжения
необходимо использовать формулу
Тетмайера-Ясинского
![]() .
Значение
критической силы сжатого стержня найдем
из выражения
.
Значение
критической силы сжатого стержня найдем
из выражения
![]() После
вычислений получим
После
вычислений получим
![]()
ЗАДАНИЕ N 16 Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Стержень длиной l круглого сечения диаметром d сжимается силой F. Напряжения в стержне не превышают предела пропорциональности. При увеличении диаметра в два раза, при прочих равных условиях, критическое напряжение ____________ раза.
|
|
|
увеличится в 4 |
|
|
|
увеличится в 2 |
|
|
|
уменьшится в 2 |
|
|
|
уменьшится в 4 |
Решение:
Критическое
напряжение в сжатом стержне, если
напряжение в стержне не превышает
предела пропорциональности, определяется
по формуле
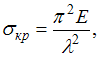 где
где
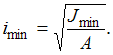 Для
круглого стержня
Для
круглого стержня ![]() При
увеличении диаметра в два раза
При
увеличении диаметра в два раза ![]() Следовательно,
при увеличении диаметра стержня в два
раза критическое напряжение увеличится
в четыре раза.
Следовательно,
при увеличении диаметра стержня в два
раза критическое напряжение увеличится
в четыре раза.
ЗАДАНИЕ
N 17 о
Тема:
Механические свойства и механические
характеристики материалов
 На
рисунке показана диаграмма растяжения
стального образца диаметром 0,01 м.
Масштаб нагрузки – 1 деление – 0,007 МН.
Предел текучести материала ____ МПа.
На
рисунке показана диаграмма растяжения
стального образца диаметром 0,01 м.
Масштаб нагрузки – 1 деление – 0,007 МН.
Предел текучести материала ____ МПа.
|
|
|
268 |
|
|
|
536 |
|
|
|
357 |
|
|
|
179 |
ЗАДАНИЕ N 18 о Тема: Продольная сила. Напряжения и деформации Продольная сила есть равнодействующая …
|
|
|
нормальных напряжений в поперечном сечении стержня |
|
|
|
внешних сил, приложенных к отсеченной части стержня |
|
|
|
нормальных напряжений и внешних сил, приложенных к отсеченной части стержня |
|
|
|
всех внешних сил, приложенных к стержню |
Решение:
 Нормальное
напряжение − это сила, приходящаяся
на единицу площади поперечного сечения.
Напряжения распределены по площади
сечения равномерно. Если их сложить, то
получим их равнодействующую – продольную
силу, которая приложена к центру тяжести
поперечного сечения.
Нормальное
напряжение − это сила, приходящаяся
на единицу площади поперечного сечения.
Напряжения распределены по площади
сечения равномерно. Если их сложить, то
получим их равнодействующую – продольную
силу, которая приложена к центру тяжести
поперечного сечения.
ЗАДАНИЕ N 19 Тема: Испытание конструкционных материалов на растяжение и сжатие Вид образца после испытаний показан на рисунке. По форме образца и характеру разрушения можно сказать, что испытание проводилось по варианту …
|
|
|
в |
|
|
|
а |
|
|
|
г |
|
|
|
б |
ЗАДАНИЕ
N 20
Тема:
Расчеты стержней на прочность и
жесткость
 Стержень
растянут осевыми силами (см. рисунок).
Задана допустимая величина нормального
напряжения
для
материала стержня. Условие прочности
имеет вид …
Стержень
растянут осевыми силами (см. рисунок).
Задана допустимая величина нормального
напряжения
для
материала стержня. Условие прочности
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Максимальные
нормальные напряжения действуют в
поперечных сечениях среднего участка,
где значение продольной силы равно 3F.
Тогда ![]() Условие
прочности для стержня имеет вид
Условие
прочности для стержня имеет вид ![]()
ЗАДАНИЕ
N 21
Тема:
Главные оси и главные моменты
инерциим
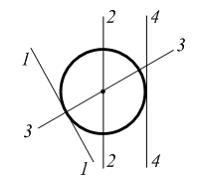 Главными
центральными осями для круга являются
оси(ось) …
Главными
центральными осями для круга являются
оси(ось) …
|
|
|
2-2, 3-3 |
|
|
|
2-2 |
|
|
|
1-1, 3-3 |
|
|
|
4-4, 2-2 |
ЗАДАНИЕ
N 22
Тема:
Статические моменты. Центр тяжести
плоской фигуры
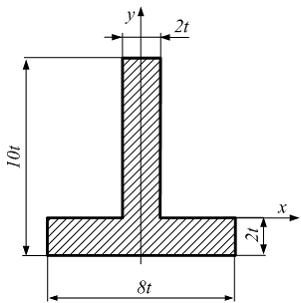 Статический
момент фигуры относительно оси x равен ____
Статический
момент фигуры относительно оси x равен ____ ![]()
|
|
|
48 |
|
|
|
80 |
|
|
|
96 |
|
|
|
102 |
Решение:
Разделим
фигуру на два прямоугольника, верхний
(I) и нижний (II).
![]() где
где ![]() и
и ![]() –
площади прямоугольников,
–
площади прямоугольников, ![]() и
и ![]() –
координаты центра тяжести прямоугольников.
–
координаты центра тяжести прямоугольников.
ЗАДАНИЕ
N 23
Тема:
Моменты инерции простых и сложных
сечений
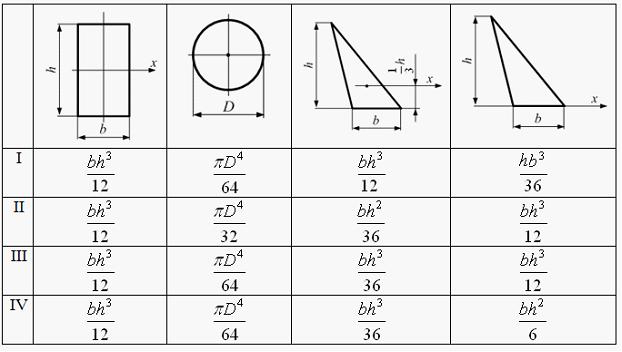 Моменты
инерции фигур относительно оси x определяются
по формулам варианта …
Моменты
инерции фигур относительно оси x определяются
по формулам варианта …
|
|
|
III |
|
|
|
II |
|
|
|
IV |
|
|
|
I |
Решение: Моменты инерции фигур относительно осей x определяются по формулам варианта III.
ЗАДАНИЕ
N 24
Тема:
Осевые моменты инерции. Зависимость
между моментами инерции при параллельном
переносе осей
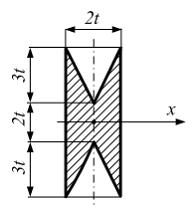 Момент
инерции фигуры относительно оси x,
проходящей через центр тяжести, равен …
Момент
инерции фигуры относительно оси x,
проходящей через центр тяжести, равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 25
Тема:
Основные понятия, определения, допущения
и принципы
 На
рисунке показаны два стержня с одинаковой
площадью поперечного сечения, работающие
на растяжение. Нормальные напряжения
в сечениях обоих стержней, достаточно
удаленных от мест приложения сил, равны
согласно …
На
рисунке показаны два стержня с одинаковой
площадью поперечного сечения, работающие
на растяжение. Нормальные напряжения
в сечениях обоих стержней, достаточно
удаленных от мест приложения сил, равны
согласно …
|
|
|
принципу Сен-Венана |
|
|
|
принципу суперпозиции |
|
|
|
принципу начальных размеров |
|
|
|
гипотезе сплошной среды |
ЗАДАНИЕ N 26 Тема: Модели прочностной надежности В курсе «Сопротивление материалов» все материалы, независимо от особенностей их микроструктуры, принято рассматривать как …
|
|
|
сплошную среду |
|
|
|
атомную кристаллическую решетку |
|
|
|
совокупность хаотически расположенных кристаллов |
|
|
|
атомную кристаллическую решетку и совокупность хаотически расположенных кристаллов |
Решение: Модель сплошной среды не учитывает: местные пустоты, инородные включения в материале, особенности кристаллической решетки и пространственную ориентацию хаотически расположенных кристаллов, что позволяет широко использовать в сопротивлении материалов аппарат высшей математики и решать практические задачи.
ЗАДАНИЕ N 27 Тема: Внутренние силы и напряжения Полное напряжение в точке сечения определяется как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Полное
напряжение в точке сечения 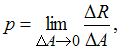 где
где ![]() –
площадь элементарной площадки вокруг
точки поперечного сечения,
–
площадь элементарной площадки вокруг
точки поперечного сечения, ![]() –
равнодействующая внутренних сил,
действующих на площадке с площадью
–
равнодействующая внутренних сил,
действующих на площадке с площадью ![]()
ЗАДАНИЕ
N 28
Тема:
Перемещение и деформация
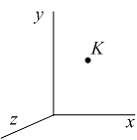 Точка К деформируемого
тела перемещается в пространстве.
Известны полное перемещение
Точка К деформируемого
тела перемещается в пространстве.
Известны полное перемещение ![]() и
перемещения вдоль координатных
осей x, y (u и v).
Величина перемещения вдоль оси z (w)
определяется по формуле …
и
перемещения вдоль координатных
осей x, y (u и v).
Величина перемещения вдоль оси z (w)
определяется по формуле …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 29 Тема: Перемещения при изгибе. Расчет балок на жесткость Консоль нагружена внешними моментами. Примерный вид изогнутой оси балки показан на схеме …
|
|
|
в |
|
|
|
а |
|
|
|
б |
|
|
|
г |
Решение: Балка имеет два силовых участка. На первом участке изгибающий момент равен. Поэтому на первом участке балка останется прямой. Второй участок испытывает деформацию чистый изгиб. Радиус кривизны оси балки во всех сечениях будет одинаков. Нижние слои балки работают на растяжение, верхние – на сжатие. Поэтому, примерный вид изогнуто оси балки соответствует схеме «в».
ЗАДАНИЕ N 30 Тема: Поперечная сила, изгибающий момент и их эпюры Балка длиной l нагружена моментом М. Поперечная сила по длине балки …
|
|
|
постоянна |
|
|
|
равна нулю |
|
|
|
меняется по линейному закону |
|
|
|
меняется по закону квадратной параболы |
Решение: Используя уравнения статики определим реакции в опорах. Затем рассекаем балку поперечным сечением на расстоянии z от правой опоры Из условия равновесия правой части найдем Поперечная сила от переменной z не зависит. Следовательно, по длине балки поперечная сила постоянна.
ЗАДАНИЕ
N 31
Тема:
Расчет балок на прочность
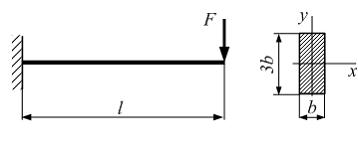 Консольная
балка прямоугольного сечения нагружена
силой
Консольная
балка прямоугольного сечения нагружена
силой ![]() Допускаемое
нормальное напряжение для материала
балки
Допускаемое
нормальное напряжение для материала
балки ![]() ,
линейный размер
,
линейный размер ![]() .
Наибольшая длина консоли
.
Наибольшая длина консоли ![]() из
расчета на прочность по нормальным
напряжениям равна ___ см.
из
расчета на прочность по нормальным
напряжениям равна ___ см.
|
|
|
64 |
|
|
|
32 |
|
|
|
128 |
|
|
|
96 |
Решение:
Условие
прочности по допускаемым нормальным
напряжениям имеет вид
![]() .
Наибольшее
нормальное напряжение действует в
сечении балки вблизи заделки, где
возникает максимальный изгибающий
момент
.
Наибольшее
нормальное напряжение действует в
сечении балки вблизи заделки, где
возникает максимальный изгибающий
момент ![]() ,
и определяется по формуле
,
и определяется по формуле  Осевой
момент сопротивления при заданных
размерах поперечного сечения
равен
Осевой
момент сопротивления при заданных
размерах поперечного сечения
равен ![]() Следовательно,
Следовательно,  Откуда
Откуда 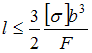 или
или ![]()
ЗАДАНИЕ N 32 Тема: Напряжения в поперечном сечении стержня при плоском изгибе Геометрическое место точек в поперечном сечении стержня при изгибе, в которых нормальные напряжения равны нулю, называется …
|
|
|
нейтральной линией |
|
|
|
нейтральным слоем |
|
|
|
ядром сечения |
|
|
|
центром изгиба |
(8)
ЗАДАНИЕ N 1 Тема: Расчет на прочность при кручении Труба скручивается двумя моментами. Величины М и заданы. Минимально допустимое значение параметра d из расчета на прочность по допускаемым напряжениям равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Запишем
условие прочности 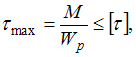 где
где 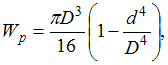 d и D –
внутренний и наружный диаметры трубы.
После вычислений получаем
d и D –
внутренний и наружный диаметры трубы.
После вычислений получаем ![]() и
условие прочности принимает вид
и
условие прочности принимает вид 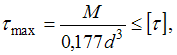 откуда
откуда 
ЗАДАНИЕ
N 2
Тема:
Крутящий момент. Деформации и
напряжения
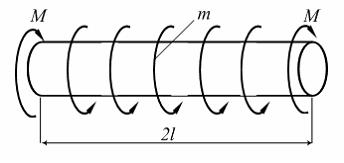 Стержень,
работающий на кручение, нагружен
равномерно распределенным по длине
моментом с интенсивностью m и
сосредоточенными моментами
Стержень,
работающий на кручение, нагружен
равномерно распределенным по длине
моментом с интенсивностью m и
сосредоточенными моментами ![]() Крутящий
момент в среднем сечении стержня, по
абсолютной величине, равен …
Крутящий
момент в среднем сечении стержня, по
абсолютной величине, равен …
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
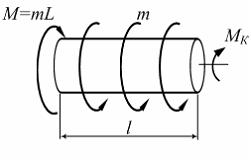 Из
условия равновесия стержня
Из
условия равновесия стержня ![]() В
среднем поперечном сечении рассекаем
стержень на две части и рассмотрим
равновесие одной из них, например, левой
(см. рисунок). Уравнение равновесия имеет
вид
В
среднем поперечном сечении рассекаем
стержень на две части и рассмотрим
равновесие одной из них, например, левой
(см. рисунок). Уравнение равновесия имеет
вид ![]() откуда
откуда ![]()
ЗАДАНИЕ N 3 Тема: Чистый сдвиг. Расчет на сдвиг (срез) На рисунке показано клеевое соединение втулки с валом, передающее крутящий момент. Задано: М, d, l, – допускаемое касательное напряжение на срез клеевого слоя. Условие прочности на срез клеевого слоя имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
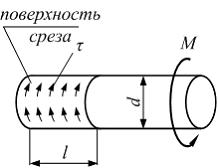 Срез
клеевого слоя происходит по цилиндрической
поверхности диаметром d и
длиной l (см. рисунок).
Считаем, что касательные напряжения
распределены по площади среза равномерно.
Запишем уравнение равновесия
Срез
клеевого слоя происходит по цилиндрической
поверхности диаметром d и
длиной l (см. рисунок).
Считаем, что касательные напряжения
распределены по площади среза равномерно.
Запишем уравнение равновесия ![]() откуда
откуда ![]() Условие
прочности на срез клеевого слоя имеет
вид
Условие
прочности на срез клеевого слоя имеет
вид ![]()
ЗАДАНИЕ
N 4
Тема:
Расчет на жесткость при кручении
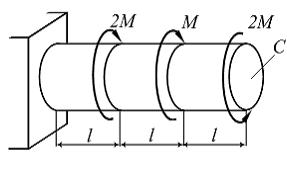 Стержень,
показанный на рисунке, испытывает
деформацию кручение.
Заданы
величины: М, l,
Стержень,
показанный на рисунке, испытывает
деформацию кручение.
Заданы
величины: М, l, ![]() ,
, ![]() –
допустимый угол поворота сечения С.
Условие жесткости имеет вид …
–
допустимый угол поворота сечения С.
Условие жесткости имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Стержень
имеет три грузовых участка (левый,
средний и правый). Крутящие моменты на
участках: ![]()
![]()
![]() Определяем
угол поворота сечения С.
Определяем
угол поворота сечения С.
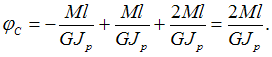 Условие
жесткости имеет вид
Условие
жесткости имеет вид 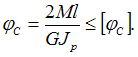
ЗАДАНИЕ N 5 Тема: Расчет балок на прочность Консольная балка длиной нагружена силой F. Сечение прямоугольное с размерами b и h. В сечении I-I максимальное нормальное напряжение равно Предел текучести для материала балки задан. Коэффициент запаса прочности по нормальным напряжениям равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Максимальное
нормальное напряжение возникает в
поперечном сечении балки вблизи заделки,
где изгибающий момент ![]() В
сечении I-I изгибающий момент
В
сечении I-I изгибающий момент ![]() Учитывая,
что форма и размеры поперечного сечения
не меняются, заключаем, что
Учитывая,
что форма и размеры поперечного сечения
не меняются, заключаем, что ![]() Коэффициент
запаса прочности по нормальным
напряжениям
Коэффициент
запаса прочности по нормальным
напряжениям 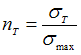 или
или ![]()
ЗАДАНИЕ
N 6
Тема:
Поперечная сила, изгибающий момент и
их эпюры
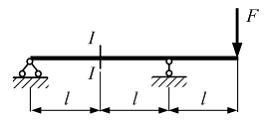 Однопролетная
консольная балка нагружена силой F.
Размер l задан.
Значения изгибающего момента и поперечной
силы по абсолютной величине в сечении
I–I равны …
Однопролетная
консольная балка нагружена силой F.
Размер l задан.
Значения изгибающего момента и поперечной
силы по абсолютной величине в сечении
I–I равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
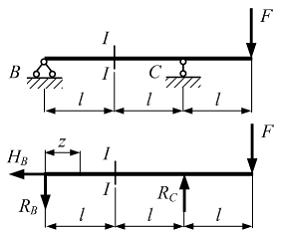 Отбросим
связи, наложенные на балку, и их действие
заменяем реакциями
Используя
уравнения статики, найдем:
Отбросим
связи, наложенные на балку, и их действие
заменяем реакциями
Используя
уравнения статики, найдем: ![]() Балка
имеет два участка. Рассекаем балку
произвольным сечением на левом участке
на две части. Отбрасываем правую часть.
Длина левой части изменяется в
пределах
Балка
имеет два участка. Рассекаем балку
произвольным сечением на левом участке
на две части. Отбрасываем правую часть.
Длина левой части изменяется в
пределах
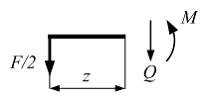 Действие
отброшенной правой части заменяем на
левую внутренними силовыми факторами.
При плоском поперечном изгибе в сечении
балки возникают два внутренних силовых
фактора: поперечная сила Q и
изгибающий момент М.
Из
уравнений статики определяем
Действие
отброшенной правой части заменяем на
левую внутренними силовыми факторами.
При плоском поперечном изгибе в сечении
балки возникают два внутренних силовых
фактора: поперечная сила Q и
изгибающий момент М.
Из
уравнений статики определяем ![]() Следовательно,
поперечная сила по длине левого участка
постоянна, а изгибающий момент меняется
по линейному закону. Сечение I–I
Следовательно,
поперечная сила по длине левого участка
постоянна, а изгибающий момент меняется
по линейному закону. Сечение I–I ![]() находится
в границах левого участка. Абсолютные
значения изгибающего момента и поперечной
силы в этом сечении:
находится
в границах левого участка. Абсолютные
значения изгибающего момента и поперечной
силы в этом сечении: ![]() .
.
ЗАДАНИЕ N 7 Тема: Перемещения при изгибе. Расчет балок на жесткость Консольная балка длиной нагружена силой F и моментом Размеры поперечного сечения по длине балки не меняются. Модуль упругости материала Е. Форма изогнутой оси балки на первом участке описывается кривой _______ порядка, а на втором _______ порядка.
|
|
|
I – третьего, II – второго |
|
|
|
I –второго, II – второго |
|
|
|
I – третьего, II – третьего |
|
|
|
I –второго, II – третьего |
ЗАДАНИЕ N 8 Тема: Напряжения в поперечном сечении стержня при плоском изгибе При плоском поперечном изгибе в точках поперечного сечения в общем случае возникают ______________ напряжения.
|
|
|
нормальные и касательные |
|
|
|
нормальные |
|
|
|
касательные |
|
|
|
главные |
Решение: При поперечном изгибе в сечении балки возникают изгибающий момент и поперечная сила. Поперечная сила является равнодействующей силой элементарных внутренних сил, лежащих в плоскости сечения. Изгибающий момент – это равнодействующий момент внутренних сил перпендикулярных плоскости сечения. Следовательно, в поперечном сечении балки, при поперечном изгибе, одновременно возникают нормальные и касательные напряжения.
ЗАДАНИЕ N 9 Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями На рисунке показано напряженное состояние в точке. Модуль упругости , коэффициент Пуассона Главные линейные деформации соответственно равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Фронтальная грань элементарного параллелепипеда является главной площадкой с главным напряжением равным нулю. Напряженное состояние чистый сдвиг. Главные напряжения при чистом сдвиге: Присваивая главным напряжениям индексы, имеем: Главные деформации определим, используя формулы обобщенного закона Гука. Подставляя числовые значения, получаем:
ЗАДАНИЕ N 10 Тема: Виды напряженного состояния На рисунке показан стержень, работающий на кручение с растяжением. Напряженное состояние в точке К является – …
|
|
|
линейное |
|
|
|
плоское |
|
|
|
объемное |
|
|
|
плоское (чистый сдвиг) |
Решение: В точке К поперечного сечения действует нормальное напряжение от силы F. Эпюра касательных напряжений от крутящего момента показана на рисунке 1. В угловых точках Поэтому напряженное состояние в точке К − линейное (одноосное растяжение, рис. 2).
ЗАДАНИЕ
N 11
Тема:
Оценка прочности материала при сложном
напряженном состоянии. Теории
прочности
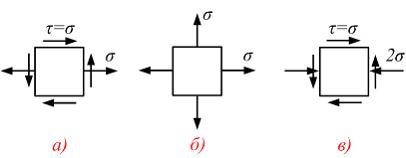 Фронтальная
грань на всех рисунках является главной
площадкой с главным напряжением, равным
нулю. Согласно гипотезе наибольших
касательных напряжений, самое опасное
напряженное состояние показано на
рисунке …
Фронтальная
грань на всех рисунках является главной
площадкой с главным напряжением, равным
нулю. Согласно гипотезе наибольших
касательных напряжений, самое опасное
напряженное состояние показано на
рисунке …
|
|
|
в |
|
|
|
а |
|
|
|
б |
|
|
|
все три напряженные состояния равноопасны |
Решение:
Во
всех напряженных состояниях одно главное
напряжение равно нулю. Два других главных
напряжения, для напряженных состояний а и в,
определяем по формуле
Вычислим
значения главных напряжений для трех
вариантов:
а) ![]()
![]()
![]() б)
б) ![]()
![]() в)
в)![]()
![]() Эквивалентные
напряжения вычисляем по
формуле
Эквивалентные
напряжения вычисляем по
формуле ![]() :
а)
:
а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() Сравнивая
эквивалентные напряжения, можно сказать,
что самое опасное напряженное состояние
показано на рисунке в.
Сравнивая
эквивалентные напряжения, можно сказать,
что самое опасное напряженное состояние
показано на рисунке в.
ЗАДАНИЕ N 12 Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) После определения величин главных напряжений им присваивают индексы 1, 2, 3, исходя из условия …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 13 Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Признаком потери устойчивости сжатого стержня при статическом нагружении является …
|
|
|
внезапная смена прямолинейной формы равновесия на криволинейную |
|
|
|
резкое уменьшение длины сжатого стержня |
|
|
|
увеличение напряжений в сжатом стержне до предела текучести |
|
|
|
увеличение напряжений в сжатом стержне до предела прочности |
Решение: Центрально сжатый стержень, при некотором значении силы, не может сохранить прямолинейную форму, а изогнется. Произойдет потеря устойчивости. Внезапная смена прямолинейной формы равновесия на криволинейную является признаком потери устойчивости стержня.
ЗАДАНИЕ
N 14
Тема:
Устойчивость за пределом пропорциональности.
Расчет сжатых стержней на
устойчивость
 Стержень
длиной
Стержень
длиной ![]() круглого
сечения диаметром
круглого
сечения диаметром ![]() сжимается
силой F.
Материал Ст.3 с характеристиками: предел
пропорциональности
сжимается
силой F.
Материал Ст.3 с характеристиками: предел
пропорциональности ![]() предел
текучести
предел
текучести ![]() модуль
упругости
модуль
упругости ![]() Значение
критического напряжения равно ____ МПа.
Значение
критического напряжения равно ____ МПа.
|
|
|
207,4 |
|
|
|
246,9 |
|
|
|
103,5 |
|
|
|
123 |
Решение:
Найдем
предельную гибкость для стержня из
данного материала
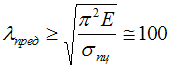 .
При
данных условиях закрепления стержня и
линейных размерах гибкость
.
При
данных условиях закрепления стержня и
линейных размерах гибкость  где
где ![]() Следовательно,
при определении критического напряжения
необходимо воспользоваться формулой
Тетмайера-Ясинского
Следовательно,
при определении критического напряжения
необходимо воспользоваться формулой
Тетмайера-Ясинского
![]() которая
справедлива, когда напряжения в сжатом
стержне больше предела пропорциональности,
но меньше предела текучести
которая
справедлива, когда напряжения в сжатом
стержне больше предела пропорциональности,
но меньше предела текучести
![]() или
или ![]() Значения
коэффициентов
Значения
коэффициентов ![]()
![]() принимаем
исходя из марки материала.
Окончательно
принимаем
исходя из марки материала.
Окончательно
![]()
ЗАДАНИЕ
N 15
Тема:
Влияние условий закрепления концов
стержня на величину критической
силы
Выражение 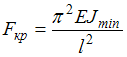 определяет
критическую силу сжатого стержня …
определяет
критическую силу сжатого стержня …
|
|
|
с шарнирно-опертыми концами |
|
|
|
при любых условиях закрепления |
|
|
|
шарнирно-опертого при наличии промежуточной опоры |
|
|
|
с одним защемленным концом и свободным другим |
Решение:
Формула
Эйлера для определения наименьшего
значения критической силы имеет
вид  Коэффициент
приведения длины
зависит
от условий закрепления стержня. Для
стержня с шарнирно-опертыми концами
Поэтому
выражение
определяет
критическую силу для сжатого стержня
с шарнирно-опертыми концами.
Коэффициент
приведения длины
зависит
от условий закрепления стержня. Для
стержня с шарнирно-опертыми концами
Поэтому
выражение
определяет
критическую силу для сжатого стержня
с шарнирно-опертыми концами.
ЗАДАНИЕ N 16 Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Стержень изготовлен из малоуглеродистой стали (предел пропорциональности модуль упругости ). Гибкость стержня Для определения критической силы сжатого стержня необходимо использовать …
|
|
|
формулу Эйлера |
|
|
|
формулу Ясинского |
|
|
|
закон Гука при сжатии |
|
|
|
формулу Энгессера |
ЗАДАНИЕ
N 17
Тема:
Расчет простейших статически неопределимых
систем
 На
рисунке показана балка прямоугольного
поперечного сечения нагруженная
моментом М.
Известны величины: l, t, E,
.
Из расчета на прочность по допускаемым
напряжениям максимально допустимое
значение М равно …
На
рисунке показана балка прямоугольного
поперечного сечения нагруженная
моментом М.
Известны величины: l, t, E,
.
Из расчета на прочность по допускаемым
напряжениям максимально допустимое
значение М равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
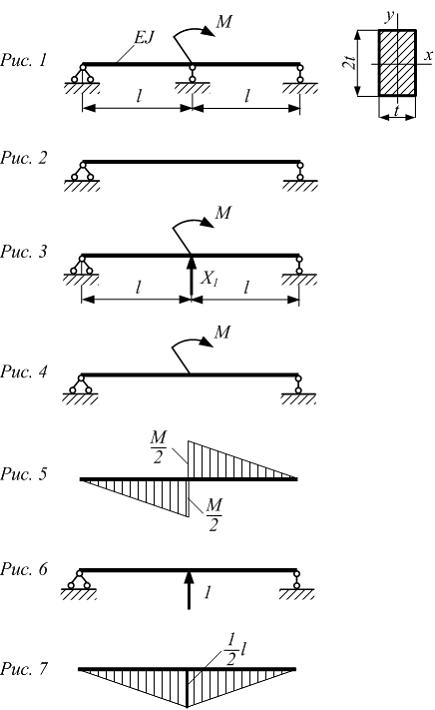 Балка
(рис. 1) один раз статически неопределима.
Для раскрытия статической неопределимости
используем метод сил. На рисунках 2 и 3
показана основная и эквивалентная
системы.
Каноническое уравнение
метода сил имеет вид
Определяем
коэффициенты канонического уравнение,
используя для вычисления интегралов
Мора способ Верещагина.
Для этого
строим эпюры изгибающих моментов
(рис. 5, 7) в грузовом и единичном
состоянии основной системы (рис. 4,
6) и перемножаем их.
Балка
(рис. 1) один раз статически неопределима.
Для раскрытия статической неопределимости
используем метод сил. На рисунках 2 и 3
показана основная и эквивалентная
системы.
Каноническое уравнение
метода сил имеет вид
Определяем
коэффициенты канонического уравнение,
используя для вычисления интегралов
Мора способ Верещагина.
Для этого
строим эпюры изгибающих моментов
(рис. 5, 7) в грузовом и единичном
состоянии основной системы (рис. 4,
6) и перемножаем их.

 После
подстановки значений
и
в
каноническое уравнение получаем
После
подстановки значений
и
в
каноническое уравнение получаем ![]() Эпюра
изгибающего момента для балки (рис. 1)
имеет вид, показанный на рисунке 5.
Условие прочности –
Эпюра
изгибающего момента для балки (рис. 1)
имеет вид, показанный на рисунке 5.
Условие прочности –  .
Откуда
.
Откуда  .
.
ЗАДАНИЕ
N 18
Тема:
Определение перемещений с помощью
интегралов Мора. Правило Верещагина
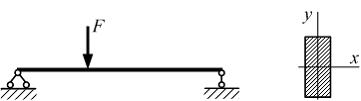 Формула
интеграла Мора, не учитывающая влияние
поперечной силы, для данной расчетной
схемы имеет вид …
Формула
интеграла Мора, не учитывающая влияние
поперечной силы, для данной расчетной
схемы имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
В
заданной расчетной схеме стержень
испытывает деформацию плоского
поперечного изгиба. Нулю не равняются
два внутренних силовых фактора: изгибающий
момент ![]() и
поперечная сила
и
поперечная сила ![]() ,
влияние которой на величину перемещения
не учитывается. Следовательно, формула
интеграла Мора для данной расчетной
схемы имеет вид
,
влияние которой на величину перемещения
не учитывается. Следовательно, формула
интеграла Мора для данной расчетной
схемы имеет вид 
ЗАДАНИЕ N 19 Тема: Метод сил Для статически неопределимой системы один из вариантов правильно выбранной основной системы показан на рисунке …
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
Решение: Система два раза статически неопределима. При выборе основной системы необходимо отбросить две дополнительные связи. На рис. 2 отброшена одна связь, на рисунках 3 и 4 удалены три связи. Правильно выбранная основная система показана на рисунке 1.
ЗАДАНИЕ N 20 Тема: Статическая неопределимость. Степень статической неопределенности Ограничения, накладываемые на взаимные смещения элементов рамы, называют ____________ связями.
|
|
|
внутренними |
|
|
|
внешними |
|
|
|
дополнительными |
|
|
|
необходимыми |
ЗАДАНИЕ N 21 Тема: Основные понятия, определения, допущения и принципы Основным объектом, изучаемым в сопротивлении материалов, является …
|
|
|
стержень |
|
|
|
пластина |
|
|
|
оболочка |
|
|
|
массивное тело |
ЗАДАНИЕ N 22 Тема: Модели прочностной надежности Материал полностью заполняет объем тела и имеет беспустотную, бездефектную структуру. Данная гипотеза называется гипотезой …
|
|
|
сплошной среды |
|
|
|
однородности |
|
|
|
изотропности |
|
|
|
абсолютной упругости |
ЗАДАНИЕ N 23 Тема: Внутренние силы и напряжения Размерность напряжения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 24 Тема: Перемещение и деформация На рисунке показано положение двух точек В и С до приложения к телу внешней нагрузки. После нагружения тела точки перемещаются в новое положение и Расстояние S между точками изменяется на величину Линейная деформация в точке В по направлению отрезка ВСопределяется как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Линейная
деформация в точке В по
направлению отрезка ВС определяется
как ![]()
ЗАДАНИЕ N 25 Тема: Главные оси и главные моменты инерциим Главными центральными осями для круга являются оси(ось) …
|
|
|
2-2, 3-3 |
|
|
|
2-2 |
|
|
|
1-1, 3-3 |
|
|
|
4-4, 2-2 |
ЗАДАНИЕ N 26 Тема: Статические моменты. Центр тяжести плоской фигуры Размерность статического момента …
|
|
|
длина3 |
|
|
|
длина2 |
|
|
|
длина4 |
|
|
|
сила∙длина |
ЗАДАНИЕ N 27 Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей Момент инерции площади – величина …
|
|
|
положительная |
|
|
|
положительная или равна нулю |
|
|
|
положительная или отрицательная |
|
|
|
отрицательная или равна нулю |
ЗАДАНИЕ
N 28
Тема:
Моменты инерции простых и сложных
сечений
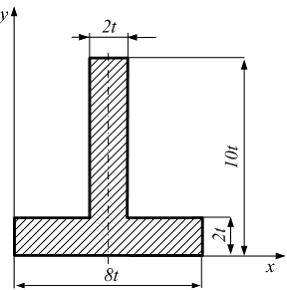 Центробежный
момент инерции фигуры относительно
осей x, y равен ____
Центробежный
момент инерции фигуры относительно
осей x, y равен ____
|
|
|
448 |
|
|
|
240 |
|
|
|
542 |
|
|
|
389 |
Решение:
 Разделим
фигуру на два прямоугольника и используем
формулу параллельного переноса.
Разделим
фигуру на два прямоугольника и используем
формулу параллельного переноса.
![]() где
где ![]()
![]()
![]()
![]() –
координаты центра тяжести прямоугольников;
–
координаты центра тяжести прямоугольников; ![]() –
площади прямоугольников;
–
площади прямоугольников; ![]() –
центробежные моменты инерции
прямоугольников относительно своих
главных центральных осей. Подставляя
в формулу числовые значения, получаем
–
центробежные моменты инерции
прямоугольников относительно своих
главных центральных осей. Подставляя
в формулу числовые значения, получаем ![]()
ЗАДАНИЕ N 29 Тема: Продольная сила. Напряжения и деформации Для определения продольной силы в поперечном сечении стержня используется метод …
|
|
|
сечений |
|
|
|
сил |
|
|
|
интегралов Мора |
|
|
|
аппроксимаций |
ЗАДАНИЕ N 30 Тема: Механические свойства и механические характеристики материалов Для хрупких материалов за опасное (предельное) напряжение принимается предел …
|
|
|
прочности |
|
|
|
пропорциональности |
|
|
|
текучести |
|
|
|
выносливости |
ЗАДАНИЕ N 31 Тема: Испытание конструкционных материалов на растяжение и сжатие Вид образца из пластичного материала после испытаний на сжатие показан на рисунке …
|
|
|
d |
|
|
|
a |
|
|
|
b |
|
|
|
c |
Решение: Образец из пластичного материала при испытании на сжатие не разрушается, а только расплющивается, что и показано на рисунке «d».
ЗАДАНИЕ
N 32
Тема:
Расчеты стержней на прочность и
жесткость
 Абсолютно
жесткий элемент СК подвешен
на двух стержнях и нагружен
силой F (см. рисунок).
Известны величины: сила F,
линейный размер l,
–
допускаемое напряжение для материала
стержней. Вес элемента СК в
расчетах не учитывается. Минимально
допустимые размеры поперечных сечений
стержней имеют значения: d = ___, t = ___.
Абсолютно
жесткий элемент СК подвешен
на двух стержнях и нагружен
силой F (см. рисунок).
Известны величины: сила F,
линейный размер l,
–
допускаемое напряжение для материала
стержней. Вес элемента СК в
расчетах не учитывается. Минимально
допустимые размеры поперечных сечений
стержней имеют значения: d = ___, t = ___.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
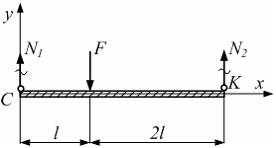 Рассмотрим
равновесие элемента СК (см. рисунок).
Уравнения равновесия имеют
вид:
Рассмотрим
равновесие элемента СК (см. рисунок).
Уравнения равновесия имеют
вид:
![]()
![]() откуда
откуда ![]()
![]() Условия
прочности для стержней:
Условия
прочности для стержней:
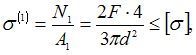
 Следовательно,
Следовательно,
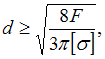
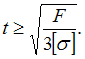
(9)
ЗАДАНИЕ
N 1
Тема:
Напряженное состояние в точке. Главные
площадки и главные напряжения)
 На
рисунке показан элементарный параллелепипед
и напряжения на его гранях:
На
рисунке показан элементарный параллелепипед
и напряжения на его гранях: ![]()
![]()
![]() Положение
главных площадок, параллельных оси z,
определяется углом равным …
Положение
главных площадок, параллельных оси z,
определяется углом равным …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2 Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Стержень растянут усилиями, равномерно распределенными по его торцам с интенсивностью р. Модуль упругости Е и коэффициент Пуассона материала стержня известны. Относительное изменение объема стержня равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 3
Тема:
Виды напряженного состояния
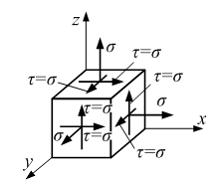 Напряженное
состояние элементарного объема,
показанное на рисунке, является – …
Напряженное
состояние элементарного объема,
показанное на рисунке, является – …
|
|
|
линейное (одноосное растяжение) |
|
|
|
плоское |
|
|
|
линейное (одноосное сжатие) |
|
|
|
объемное |
Решение:
Главные
напряжения являются корнями кубического
уравнения
![]() где:
где:
![]()
![]()
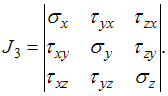 В
нашем случае
В
нашем случае ![]() ,
и кубическое уравнение принимает
вид
,
и кубическое уравнение принимает
вид ![]() откуда
откуда ![]()
![]()
![]() Таким
образом, напряженное состояние
элементарного объема линейное (одноосное
растяжение).
Таким
образом, напряженное состояние
элементарного объема линейное (одноосное
растяжение).
ЗАДАНИЕ N 4 Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности На рисунке показано напряженное состояние в точке. Материал пластичный с пределом текучести Для перехода материала из упругого состояния в пластичное компоненты напряженного состояния следует увеличить в _____ раз(-а). Использовать теорию наибольших касательных напряжений.
|
|
|
4,5 |
|
|
|
9 |
|
|
|
3 |
|
|
|
5,3 |
Решение:
Главные
напряжения: ![]() Эквивалентное
напряжение
Эквивалентное
напряжение ![]() Коэффициент
запаса
Коэффициент
запаса  Для
перехода материала из упругого состояния
в пластичное напряжения
Для
перехода материала из упругого состояния
в пластичное напряжения ![]() следует
увеличить в 4,5 раза.
следует
увеличить в 4,5 раза.
ЗАДАНИЕ
N 5
Тема:
Поперечная сила, изгибающий момент и
их эпюры
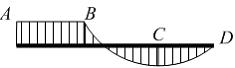 Эпюра
изгибающих моментов показана на рисунке.
В отношении действующей на балку
нагрузки, неверным является
утверждение, что …
Эпюра
изгибающих моментов показана на рисунке.
В отношении действующей на балку
нагрузки, неверным является
утверждение, что …
|
|
|
в сечении В к балке приложен сосредоточенный момент |
|
|
|
на участке BD действует распределенная нагрузка |
|
|
|
в сечении А к балке приложен сосредоточенный момент |
|
|
|
в сечении В начинается распределенная нагрузка |
Решение: Известно, что в сечении балки, в котором приложен сосредоточенный момент, на эпюре изгибающих моментов будет скачок на величину этого момента. В сечении В отсутствует скачок на эпюре. Следовательно, в отношении действующей на балку нагрузки, неверным будет утверждение, что в сечении В к балке приложен сосредоточенный момент.
ЗАДАНИЕ
N 6
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
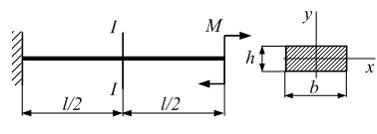 Консольная
балка длиной
Консольная
балка длиной ![]() нагружена
моментом
нагружена
моментом ![]() Поперечное
сечение балки прямоугольник:
Поперечное
сечение балки прямоугольник: ![]()
![]() Модуль
упругости материала
Модуль
упругости материала ![]() Радиус
кривизны балки в сечении I–I равен ___ (м).
Радиус
кривизны балки в сечении I–I равен ___ (м).
|
|
|
3,6 |
|
|
|
6 |
|
|
|
5,2 |
|
|
|
4,8 |
Решение:
Балка
испытывает чистый изгиб. Значение
изгибающего момента в любом
сечении ![]() Следовательно,
балка изгибается по окружности. Для
определения радиуса кривизны воспользуемся
формулой
Следовательно,
балка изгибается по окружности. Для
определения радиуса кривизны воспользуемся
формулой
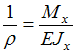 ,
откуда
,
откуда 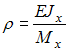 .
–
жесткость поперечного сечения балки
на изгиб. Осевой момент инерции
сечения
.
–
жесткость поперечного сечения балки
на изгиб. Осевой момент инерции
сечения 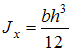 .
После
вычислений найдем
.
После
вычислений найдем ![]()
ЗАДАНИЕ N 7 Тема: Расчет балок на прочность Консольная балка длиной нагружена равномерно распределенной нагрузкой интенсивности Поперечное сечение – равнобедренный треугольник. Допускаемое нормальное напряжение для материала балки Из расчета на прочность по нормальным напряжениям размер поперечного сечения балки b равен ____ (см).
|
|
|
3 |
|
|
|
5 |
|
|
|
4 |
|
|
|
6 |
Решение:
Максимальные
нормальные напряжения в балке определяются
по формуле  В
случае, когда размеры поперечного
сечения балки по длине не меняются,
максимальные нормальные напряжения
возникают в сечении балки, где действует
максимальный изгибающий момент и в
точках, наиболее удаленных от нейтральной
линии. Нейтральная линия совпадает с
главной центральной осью поперечного
сечения перпендикулярной плоскости
действия изгибающего момента. Максимальный
изгибающий момент
В
случае, когда размеры поперечного
сечения балки по длине не меняются,
максимальные нормальные напряжения
возникают в сечении балки, где действует
максимальный изгибающий момент и в
точках, наиболее удаленных от нейтральной
линии. Нейтральная линия совпадает с
главной центральной осью поперечного
сечения перпендикулярной плоскости
действия изгибающего момента. Максимальный
изгибающий момент ![]() действует
в сечении балки вблизи заделки. Центр
тяжести треугольного сечения расположен
на расстоянии
действует
в сечении балки вблизи заделки. Центр
тяжести треугольного сечения расположен
на расстоянии ![]() от
основания треугольника, то есть
от
основания треугольника, то есть ![]() Осевой
момент инерции относительно главной
центральной оси x равен
Осевой
момент инерции относительно главной
центральной оси x равен  а
расстояние
а
расстояние ![]() После
вычислений
После
вычислений  Из
условия прочности по нормальным
напряжениям
Из
условия прочности по нормальным
напряжениям ![]() получим
получим ![]()
ЗАДАНИЕ
N 8
Тема:
Напряжения в поперечном сечении стержня
при плоском изгибе
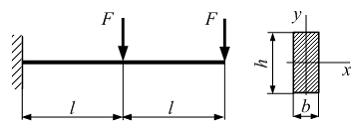 Консольная
балка прямоугольного сечения с
размерами b и h нагружена
силами F.
Линейный размер
Консольная
балка прямоугольного сечения с
размерами b и h нагружена
силами F.
Линейный размер ![]() .
Отношение максимального нормального
напряжения к максимальному касательному
напряжению в балке
.
Отношение максимального нормального
напряжения к максимальному касательному
напряжению в балке ![]() равно …
равно …
|
|
|
60 |
|
|
|
40 |
|
|
|
80 |
|
|
|
10 |
Решение:
Максимальный
изгибающий момент возникает в поперечном
сечении балки вблизи заделки ![]() Для
определения максимального нормального
напряжения используем
формулу
где
Для
определения максимального нормального
напряжения используем
формулу
где  Тогда
Тогда 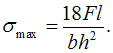 Максимальное
значение поперечной силы
Максимальное
значение поперечной силы ![]() Максимальное
касательное напряжение для балки
прямоугольного сечения определяется
по формуле
Максимальное
касательное напряжение для балки
прямоугольного сечения определяется
по формуле 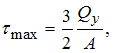 где
где ![]() После
вычислений
После
вычислений ![]() Учитывая,
что
,
получим
Учитывая,
что
,
получим 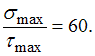
ЗАДАНИЕ N 9 Тема: Продольная сила. Напряжения и деформации Продольная сила есть равнодействующая …
|
|
|
нормальных напряжений в поперечном сечении стержня |
|
|
|
внешних сил, приложенных к отсеченной части стержня |
|
|
|
нормальных напряжений и внешних сил, приложенных к отсеченной части стержня |
|
|
|
всех внешних сил, приложенных к стержню |
Решение: Нормальное напряжение − это сила, приходящаяся на единицу площади поперечного сечения. Напряжения распределены по площади сечения равномерно. Если их сложить, то получим их равнодействующую – продольную силу, которая приложена к центру тяжести поперечного сечения.
ЗАДАНИЕ N 10 Тема: Испытание конструкционных материалов на растяжение и сжатие Вид образца после испытаний показан на рисунке. По форме образца и характеру разрушения можно сказать, что испытание проводилось по варианту …
|
|
|
в |
|
|
|
а |
|
|
|
г |
|
|
|
б |
ЗАДАНИЕ N 11 Тема: Механические свойства и механические характеристики материалов На рисунке показана диаграмма сжатия чугунного образца диаметром 15 мм. Масштаб нагрузки – 1 деление – 0,02 МН. Предел прочности чугуна при сжатии равен ____ МПа.
|
|
|
678 |
|
|
|
565 |
|
|
|
700 |
|
|
|
860 |
Решение: Предел прочности чугуна при сжатии определим по формуле где Подставляя числовые значения, получаем
ЗАДАНИЕ
N 12
Тема:
Расчеты стержней на прочность и
жесткость
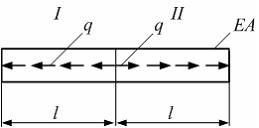 На
стержень действует равномерно
распределенная нагрузка с
интенсивностью q (см. рисунок).
Заданы величины:
На
стержень действует равномерно
распределенная нагрузка с
интенсивностью q (см. рисунок).
Заданы величины: ![]() –
допустимая величина удлинения стержня.
Максимально допустимое значение
интенсивности распределенной нагрузки
равно …
–
допустимая величина удлинения стержня.
Максимально допустимое значение
интенсивности распределенной нагрузки
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
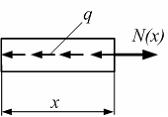 Стержень
имеет два грузовых участка. Поперечным
сечением на первом участке делим стержень
на две части и рассмотрим равновесие
левой части (см. рисунок). Уравнение
равновесия имеет вид
Стержень
имеет два грузовых участка. Поперечным
сечением на первом участке делим стержень
на две части и рассмотрим равновесие
левой части (см. рисунок). Уравнение
равновесия имеет вид ![]() откуда
откуда ![]() Абсолютное
удлинение первого участка
Абсолютное
удлинение первого участка 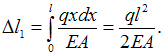 Удлинение
всего стержня
Удлинение
всего стержня 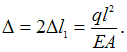 Условие
жесткости имеет вид
Условие
жесткости имеет вид  откуда
откуда ![]()
ЗАДАНИЕ
N 13
Тема:
Формула Эйлера для критической силы
сжатого стержня и пределы ее
применимости
Стержень
с площадью поперечного сечения А сжимается
силой приложенной в центре тяжести
поперечного сечения. Предел
пропорциональности ![]() предел
текучести
предел
текучести ![]() предел
прочности на сжатие
предел
прочности на сжатие ![]() для
материала заданы. Для определения
критической силы формула Эйлера применима
при выполнении условия …
для
материала заданы. Для определения
критической силы формула Эйлера применима
при выполнении условия …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 14
Тема:
Устойчивость за пределом пропорциональности.
Расчет сжатых стержней на
устойчивость
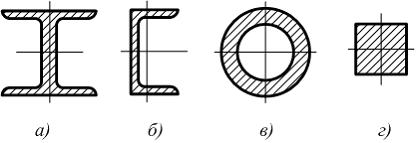 Площади
поперечных сечений, представленных на
схемах, одинаковы. С точки зрения
устойчивости наиболее рациональная
форма показана на схеме …
Площади
поперечных сечений, представленных на
схемах, одинаковы. С точки зрения
устойчивости наиболее рациональная
форма показана на схеме …
|
|
|
в |
|
|
|
г |
|
|
|
а |
|
|
|
б |
Решение: С позиции устойчивости сжатого стержня необходимо конструировать сечение таким образом, чтобы при определенной площади величина наименьшего радиуса инерции была бы возможно большей. Также желательно стремиться к получению, при данной площади, наибольших центральных моментов инерции. Этим двум условиям удовлетворяет трубчатое сечение, показанное на схеме «в».
ЗАДАНИЕ N 15 Тема: Влияние условий закрепления концов стержня на величину критической силы Стержни изготовлены из одного материала, имеют одинаковую длину, форму и размеры поперечного сечения. Схемы закрепления стержней, сжатых силой F, показаны на рисунках. Наибольшее значение гибкости имеет стержень, показанный на рисунке …
|
|
|
а |
|
|
|
г |
|
|
|
в |
|
|
|
б |
ЗАДАНИЕ N 16 Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Стержень длиной l сжимается силой F приложенной в центре тяжести поперечного сечения. При увеличении длины стержня в два раза, при прочих равных условиях, критическое напряжение … При решении учитывать, что напряжения в сжатом стержне не превышают предел пропорциональности.
|
|
|
уменьшается в 4 раза |
|
|
|
увеличивается в 4 раза |
|
|
|
уменьшается в 2 раза |
|
|
|
увеличивается в 2 раза |
ЗАДАНИЕ N 17 Тема: Расчет на жесткость при кручении Стержень скручивается двумя моментами (см. рисунок). Из расчетов на прочность и жесткость максимально допустимая величина момента М равна ____
|
|
|
0,0013 |
|
|
|
0,0098 |
|
|
|
0,0056 |
|
|
|
0,0008 |
Решение: Запишем условие прочности для стержня откуда Составим условие жесткости откуда Таким образом, максимально допустимое значение
ЗАДАНИЕ N 18 Тема: Крутящий момент. Деформации и напряжения При кручении стержня круглого поперечного сечения угол сдвига изменяется вдоль радиуса по …
|
|
|
линейному закону |
|
|
|
по закону синуса |
|
|
|
по закону квадратной параболы |
|
|
|
по закону косинуса |
ЗАДАНИЕ
N 19
Тема:
Чистый сдвиг. Расчет на сдвиг (срез)
 На
рисунке показано клеевое соединение
трех листов. Известно:
На
рисунке показано клеевое соединение
трех листов. Известно: ![]()
![]()
![]() –
допускаемое касательное напряжение на
срез клеевого слоя. Максимально допустимое
значение силы F из
расчета на срез клеевого слоя равно ___ кН.
–
допускаемое касательное напряжение на
срез клеевого слоя. Максимально допустимое
значение силы F из
расчета на срез клеевого слоя равно ___ кН.
|
|
|
14,4 |
|
|
|
7,2 |
|
|
|
3,6 |
|
|
|
5,2 |
ЗАДАНИЕ N 20 Тема: Расчет на прочность при кручении Стержень круглого поперечного сечения из пластичного материала работает на кручение. При расчете по допускаемым касательным напряжениям за предельное напряжение принимается …
|
|
|
предел текучести при чистом сдвиге |
|
|
|
предел текучести при растяжении |
|
|
|
предел прочности при чистом сдвиге |
|
|
|
предел упругости при чистом сдвиге |
Решение: Предел текучести при чистом сдвиге считается предельным напряжением в расчетах по допускаемым напряжениям стержней из пластичного материала, работающих на кручение.
ЗАДАНИЕ N 21 Тема: Расчет простейших статически неопределимых систем На рисунке показана балка прямоугольного поперечного сечения нагруженная моментом М. Известны величины: l, t, E, . Из расчета на прочность по допускаемым напряжениям максимально допустимое значение М равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Балка (рис. 1) один раз статически неопределима. Для раскрытия статической неопределимости используем метод сил. На рисунках 2 и 3 показана основная и эквивалентная системы. Каноническое уравнение метода сил имеет вид Определяем коэффициенты канонического уравнение, используя для вычисления интегралов Мора способ Верещагина. Для этого строим эпюры изгибающих моментов (рис. 5, 7) в грузовом и единичном состоянии основной системы (рис. 4, 6) и перемножаем их. После подстановки значений и в каноническое уравнение получаем Эпюра изгибающего момента для балки (рис. 1) имеет вид, показанный на рисунке 5. Условие прочности – . Откуда .
ЗАДАНИЕ
N 22
Тема:
Метод сил
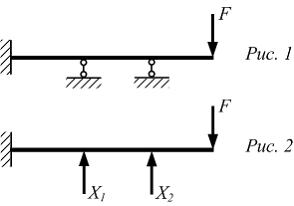 На
рисунках 1 и 2 показаны два раза статически
неопределимая балка и эквивалентная
система метода сил. Система канонических
уравнений имеет вид
На
рисунках 1 и 2 показаны два раза статически
неопределимая балка и эквивалентная
система метода сил. Система канонических
уравнений имеет вид
![]()
![]() Левые
части уравнений приравниваются к нулю
потому, что …
Левые
части уравнений приравниваются к нулю
потому, что …
|
|
|
шарнирно подвижные опоры жесткие |
|
|
|
перемещения поперечных сечений балки малы |
|
|
|
сила F предполагается небольшой |
|
|
|
сама балка достаточно жесткая |
ЗАДАНИЕ N 23 Тема: Статическая неопределимость. Степень статической неопределенности Степень статической неопределимости плоской рамы равна …
|
|
|
четырем |
|
|
|
трем |
|
|
|
пяти |
|
|
|
двум |
ЗАДАНИЕ N 24 Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина Необходимо определить угол поворота поперечного сечения С (см. рисунок) с помощью интегралов Мора, который требуется вычислить способом Верещагина. Правильная эпюра изгибающего момента в единичном состоянии, построенная на сжатом слое, имеет вид …
|
|
|
в |
|
|
|
г |
|
|
|
б |
|
|
|
а |
Решение: Единичное состояние для определения угла поворота сечения С и эпюра изгибающего момента показаны на рисунке.
ЗАДАНИЕ
N 25
Тема:
Главные оси и главные моменты
инерциим
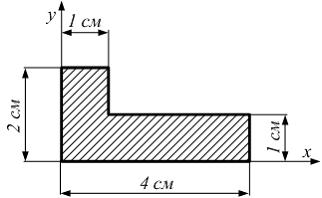 Моменты
инерции фигуры относительно
осей x и y:
Моменты
инерции фигуры относительно
осей x и y: ![]()
![]()
![]() Положение
главных осей, проходящих через начало
координат, определяется углом равным …
Положение
главных осей, проходящих через начало
координат, определяется углом равным …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
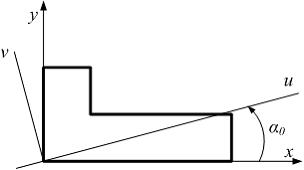 Угол
между главной осью и положительным
направлением оси x определим
по формуле
Угол
между главной осью и положительным
направлением оси x определим
по формуле 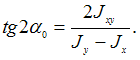 После
вычислений получаем
После
вычислений получаем ![]() и
откладываем его против часовой стрелки
(см. рисунок). Оси u и v –
главные оси, проходящие через начало
координат.
и
откладываем его против часовой стрелки
(см. рисунок). Оси u и v –
главные оси, проходящие через начало
координат.
ЗАДАНИЕ N 26 Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей Осевой момент инерции поперечного сечения двутавра №10 относительно оси равен ___ Характеристики двутавра взять из ГОСТа.
|
|
|
498 |
|
|
|
300 |
|
|
|
258 |
|
|
|
320 |
ЗАДАНИЕ
N 27
Тема:
Статические моменты. Центр тяжести
плоской фигуры
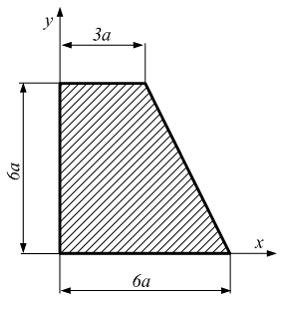 Координаты
центра тяжести трапеции (см. рис.) в
заданной системе координат
Координаты
центра тяжести трапеции (см. рис.) в
заданной системе координат ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
 Разобьем
сложную фигуру на простые фигуры, площади
которых можно вычислить и положения
центров тяжести которых известны. В
данном случае это прямоугольник и
треугольник. Координаты центра тяжести
трапеции определим по
формулам
Разобьем
сложную фигуру на простые фигуры, площади
которых можно вычислить и положения
центров тяжести которых известны. В
данном случае это прямоугольник и
треугольник. Координаты центра тяжести
трапеции определим по
формулам  где
где ![]() − статические
моменты площади трапеции относительно
осей y и x, А –
площадь трапеции.
− статические
моменты площади трапеции относительно
осей y и x, А –
площадь трапеции.

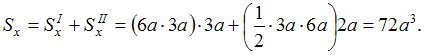
![]() Подставляя
найденные значения
Подставляя
найденные значения ![]() в
формулы для определения
в
формулы для определения ![]() и
и ![]() получаем
получаем
![]()
ЗАДАНИЕ
N 28
Тема:
Моменты инерции простых и сложных
сечений
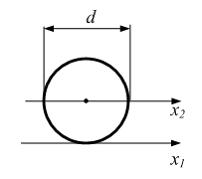 Ось
перемещается из положения x1 в
положение x2.
Момент инерции круга при этом …
Ось
перемещается из положения x1 в
положение x2.
Момент инерции круга при этом …
|
|
|
уменьшается
на величину |
|
|
|
увеличивается на величину |
|
|
|
уменьшается
на величину |
|
|
|
увеличивается на величину |
Решение:
Формула,
связывающая моменты инерции относительно
параллельных осей, одна из которых
центральная, имеет вид
![]() где а –
расстояние между осями, А –
площадь фигуры.
При перемещении оси
из положения x1 в
положение x2 момент
инерции уменьшается на величину
где а –
расстояние между осями, А –
площадь фигуры.
При перемещении оси
из положения x1 в
положение x2 момент
инерции уменьшается на величину 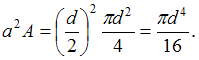
ЗАДАНИЕ N 29 Тема: Основные понятия, определения, допущения и принципы Свойство материала сохранять некоторую часть деформации после снятия нагрузки называется …
|
|
|
пластичностью |
|
|
|
упругостью |
|
|
|
жесткостью |
|
|
|
твердостью |
Решение:
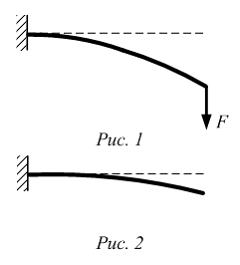 При
нагружении силой F стержень
изгибается (рис. 1). В процессе снятия
нагрузки (при уменьшении силы F)
исчезает только часть деформаций. Такие
деформации называются упругими
деформациями. Деформации, которые
сохранились после снятия нагрузки,
называются пластическими деформациями.
В результате стержень после снятия
нагрузки остается искривленным. Если
сила F мала,
то пластические деформации равны нулю
и стержень после снятия нагрузки
полностью выпрямляется. Свойство
материала сохранять некоторую часть
деформации после снятия нагрузки
называется пластичностью.
При
нагружении силой F стержень
изгибается (рис. 1). В процессе снятия
нагрузки (при уменьшении силы F)
исчезает только часть деформаций. Такие
деформации называются упругими
деформациями. Деформации, которые
сохранились после снятия нагрузки,
называются пластическими деформациями.
В результате стержень после снятия
нагрузки остается искривленным. Если
сила F мала,
то пластические деформации равны нулю
и стержень после снятия нагрузки
полностью выпрямляется. Свойство
материала сохранять некоторую часть
деформации после снятия нагрузки
называется пластичностью.
ЗАДАНИЕ N 30 Тема: Модели прочностной надежности В сопротивлении материалов все тела считаются …
|
|
|
абсолютно упругими |
|
|
|
абсолютно твердыми |
|
|
|
вязко-упругими |
|
|
|
упруго-вязко-пластичными |
Решение: Свойство тела восстанавливать свою форму и размеры после снятия нагрузки называется упругостью. При решении большинства задач в сопротивлении материалов все тела считаются абсолютно упругими.
ЗАДАНИЕ N 31 Тема: Перемещение и деформация На рисунке показано положение двух точек В и С до приложения к телу внешней нагрузки. После нагружения тела точки перемещаются в новое положение и Расстояние S между точками изменяется на величину Линейная деформация в точке В по направлению отрезка ВСопределяется как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 32 Тема: Внутренние силы и напряжения Интегральная связь между крутящим моментом ( ) и касательными напряжениями имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Площадь сечения можно разбить прямоугольной координатной сеткой на элементарные площадки. и – равнодействующие касательных напряжений, действующих на элементарной площадке, − элементарные моменты относительно оси z. Крутящий момент определяется как сумма элементарных моментов. Заменяя суммирование интегрированием по площади сечения, получаем
(10)
ЗАДАНИЕ N 1 Тема: Напряжения в поперечном сечении стержня при плоском изгибе Консольная балка длиной l имеет два варианта расположения прямоугольного поперечного сечения. Сила F, линейные размеры b и h заданы. В опасном сечении балки отношение наибольших нормальных напряжений равно …
|
|
|
2 |
|
|
|
1 |
|
|
|
6 |
|
|
|
4 |
ЗАДАНИЕ N 2 Тема: Расчет балок на прочность Однопролетная деревянная балка длиной нагружена равномерно распределенной нагрузкой интенсивности q. Диаметр поперечного сечения Значение допускаемого нормального напряжения Из расчета на прочность по нормальным напряжениям максимально допустимое значение интенсивности нагрузки q равно ____
|
|
|
5,88 |
|
|
|
5,58 |
|
|
|
6,24 |
|
|
|
4,68 |
ЗАДАНИЕ
N 3
Тема:
Поперечная сила, изгибающий момент и
их эпюры
 На
рисунке показана эпюра поперечных сил.
Правильным является утверждение, что …
На
рисунке показана эпюра поперечных сил.
Правильным является утверждение, что …
|
|
|
в сечении А к балке приложена сосредоточенная сила |
|
|
|
на участке АВ действует распределенная нагрузка |
|
|
|
в сечении В на эпюре изгибающих моментов отсутствует излом |
|
|
|
участок ВС свободен от распределенной нагрузки |
Решение: В сечении, где к балке приложена сосредоточенная сила, на эпюре поперечной сила будет скачок на величину и в направлении этой силы. Следовательно, правильным является утверждение, что в сечении А к балке приложена сосредоточенная сила.
ЗАДАНИЕ
N 4
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
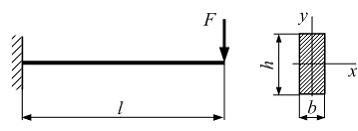 Консоль
длиной l нагружена
силой F.
Сечение балки прямоугольное с
размерами b и h.
Модуль упругости материала Е.
При увеличении линейных размеров
Консоль
длиной l нагружена
силой F.
Сечение балки прямоугольное с
размерами b и h.
Модуль упругости материала Е.
При увеличении линейных размеров ![]() в
два раза значение максимального прогиба …
в
два раза значение максимального прогиба …
|
|
|
уменьшится в 2 раза |
|
|
|
увеличится в 2 раза |
|
|
|
не изменится |
|
|
|
увеличится в 4 раза |
ЗАДАНИЕ N 5 Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Если то линейные деформации:
|
|
|
0; 0; 0 |
|
|
|
0; 0; 0,0015 |
|
|
|
0,0025; 0,0025; 0,0025 |
|
|
|
0,062; 0; 0 |
Решение: Согласно обобщенному закону Гука, линейные деформации элементарного объема зависят только от нормальных напряжений, действующих на его гранях. Поэтому в нашем случае
ЗАДАНИЕ N 6 Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) Нормальные напряжения, действующие на главных площадках, называются …
|
|
|
главными напряжениями |
|
|
|
экстремальными напряжениями |
|
|
|
октаэдрическими напряжениями |
|
|
|
инвариантами напряженного состояния |
ЗАДАНИЕ N 7 Тема: Виды напряженного состояния Напряженные состояния в точках нагруженного тела бывают ______ видов.
|
|
|
трех |
|
|
|
двух |
|
|
|
четырех |
|
|
|
пяти |
Решение: Напряженные состояния в точках нагруженного тела бывают трех видов: линейное, плоское, объемное.
ЗАДАНИЕ N 8 Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности Согласно теории наибольших касательных напряжений (третья теория прочности), самое опасное напряженное состояние показано на рисунке …
|
|
|
б |
|
|
|
в |
|
|
|
а |
|
|
|
все три напряженные состояния равноопасны |
Решение: Согласно теории наибольших касательных напряжений, эквивалентное напряжение определяется по формуле Определим эквивалентное напряжение для трех вариантов: а) , б) , в) . Сравнивая эквивалентные напряжения, можно сказать, что самое опасное напряженное состояние показано на рисунке б.
ЗАДАНИЕ N 9 Тема: Механические свойства и механические характеристики материалов Материал, механические характеристики которого не зависят от направления, называется …
|
|
|
изотропным |
|
|
|
однородным |
|
|
|
сплошным |
|
|
|
анизотропным |
ЗАДАНИЕ N 10 Тема: Расчеты стержней на прочность и жесткость На стержень действует равномерно распределенная нагрузка с интенсивностью q (см. рисунок). Заданы величины: – допустимая величина удлинения стержня. Максимально допустимое значение интенсивности распределенной нагрузки равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 11 Тема: Испытание конструкционных материалов на растяжение и сжатие Стрелка рычажного тензометра показывает на шкале …
|
|
|
абсолютное увеличение (уменьшение) расстояния между ножами тензометра в числе делений |
|
|
|
абсолютное изменение размера поперечного сечения образца |
|
|
|
относительное удлинение образца |
|
|
|
относительное изменение расстояния между ножами тензометра |
ЗАДАНИЕ N 12 Тема: Продольная сила. Напряжения и деформации Значение продольной силы в сечении С-С равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Сечением С-С делим стержень на две части. Для того чтобы определить продольную силу в сечении, следует рассмотреть равновесие одной из частей. Рассмотрим, например, равновесие левой части (см. рисунок). Продольную силу N направляем от сечения, полагая, что она растягивает материал участка. Уравнение равновесия имеет вид откуда
ЗАДАНИЕ N 13 Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости График зависимости критического напряжения от гибкости сжатого стержня, в пределах применимости формулы Эйлера, представляет …
|
|
|
гиперболу |
|
|
|
параболу |
|
|
|
синусоиду |
|
|
|
прямую линию |
Решение:
Величина
критического напряжения есть отношение
критической силы к площади поперечного
сечения
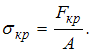 Значение
критической силы сжатого стержня по
формуле Эйлера определяется из
выражения
Значение
критической силы сжатого стержня по
формуле Эйлера определяется из
выражения
 тогда
тогда
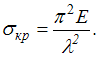 Из
формулы следует, что график зависимости
критического напряжения от гибкости
сжатого стержня представляет гиперболу.
Из
формулы следует, что график зависимости
критического напряжения от гибкости
сжатого стержня представляет гиперболу.
ЗАДАНИЕ N 14 Тема: Влияние условий закрепления концов стержня на величину критической силы Шарнирно-опертый по концам стержень длиной l сжимается силой F. При постановке в середине пролета промежуточной опоры значение гибкости …
|
|
|
уменьшится в 2 раза |
|
|
|
не изменится |
|
|
|
увеличится в 2 раза |
|
|
|
уменьшится в 4 раза |
Решение: Гибкость стержня определяется по формуле При прочих равных условиях значение гибкости зависит от коэффициента приведения длины До постановки промежуточной опоры после постановки Значение гибкости уменьшится в 2 раза.
ЗАДАНИЕ N 15 Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость График зависимости критических напряжений от гибкости стержня изготовленного из стали, когда напряжения в сжатом стержне больше предела пропорциональности, но меньше предела текучести, имеет вид …
|
|
|
наклонной прямой |
|
|
|
гиперболы |
|
|
|
горизонтальной прямой |
|
|
|
полуволны синусоиды |
ЗАДАНИЕ N 16 Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Стержень длиной l сжимается силой F приложенной в центре тяжести поперечного сечения. При увеличении длины стержня в два раза, при прочих равных условиях, критическое напряжение … При решении учитывать, что напряжения в сжатом стержне не превышают предел пропорциональности.
|
|
|
уменьшается в 4 раза |
|
|
|
увеличивается в 4 раза |
|
|
|
уменьшается в 2 раза |
|
|
|
увеличивается в 2 раза |
Решение:
Напряжения
в стержне не превышают предел
пропорциональности. Поэтому, при
определении критического напряжения,
следует воспользоваться формулой  где
где  При
увеличении длины стержня в два раза,
при прочих равных условиях, гибкость
стержня
При
увеличении длины стержня в два раза,
при прочих равных условиях, гибкость
стержня ![]() увеличивается
в два раза, а критическое
напряжение
увеличивается
в два раза, а критическое
напряжение ![]() уменьшается
в четыре раза.
уменьшается
в четыре раза.
ЗАДАНИЕ
N 17
Тема:
Основные понятия, определения, допущения
и принципы
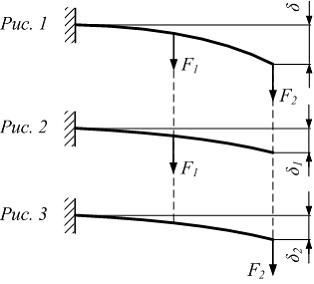 На
рисунках показана одна и та же балка,
нагруженная силами
На
рисунках показана одна и та же балка,
нагруженная силами ![]() и
и ![]() (рис. 1),
силой
(рис. 2),
силой
(рис. 3).
(рис. 1),
силой
(рис. 2),
силой
(рис. 3). ![]() –
прогибы концевых сечений. Исходя из
принципа независимости действия сил
можно записать …
–
прогибы концевых сечений. Исходя из
принципа независимости действия сил
можно записать …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Согласно
принципу независимости действия сил
результатов действия системы сил равен
сумме результатов действий каждой силы
в отдельности. Поэтому можно записать ![]()
ЗАДАНИЕ
N 18
Тема:
Модели прочностной надежности
 Моделью
формы столешницы стола (см. рисунок)
является …
Моделью
формы столешницы стола (см. рисунок)
является …
|
|
|
пластина |
|
|
|
оболочка |
|
|
|
массивное тело |
|
|
|
стержень |
Решение: Пластина – это тело, ограниченное двумя плоскостями, близко расположенными друг к другу, поэтому моделью формы столешницы является пластина.
ЗАДАНИЕ N 19 Тема: Внутренние силы и напряжения Интегральная связь между крутящим моментом ( ) и касательными напряжениями имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Площадь сечения можно разбить прямоугольной координатной сеткой на элементарные площадки. и – равнодействующие касательных напряжений, действующих на элементарной площадке, − элементарные моменты относительно оси z. Крутящий момент определяется как сумма элементарных моментов. Заменяя суммирование интегрированием по площади сечения, получаем
ЗАДАНИЕ N 20 Тема: Перемещение и деформация В процессе деформации точки А, В, С деформируемого тела перемещаются в плоскости xoy и занимают положения . Прямолинейные отрезки АВ и АС поворачиваются на углы и Угловая деформация в точке А между направлениями АВ и АС, когда длины отрезков стремятся к нулю, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Угловая деформация – это изменение угла между двумя взаимно перпендикулярными до деформации малыми отрезками, проходящими через данную точку. Следовательно, угловая деформация в точке А между направлениями АВ и АС равна
ЗАДАНИЕ N 21 Тема: Расчет на жесткость при кручении На рисунке показан стержень, работающий на кручение. Величины (допускаемый угол поворота сечения С) заданы. Максимально допустимое значение момента М равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 22
Тема:
Чистый сдвиг. Расчет на сдвиг (срез)
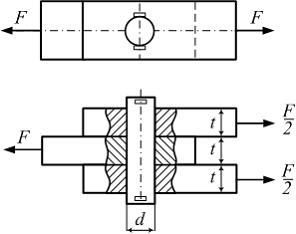 Три
металлические полосы (см. рисунок)
соединены штифтом.
Три
металлические полосы (см. рисунок)
соединены штифтом. ![]() –
значение допускаемого касательного
напряжения на срез для материала штифта.
Условие прочности штифта на срез имеет
вид …
–
значение допускаемого касательного
напряжения на срез для материала штифта.
Условие прочности штифта на срез имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
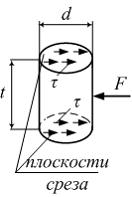 Рассмотрим
равновесие средней части штифта
(см. рисунок). Считаем, что касательные
напряжения распределены по площади
среза равномерно. Составим уравнение
равновесия
Рассмотрим
равновесие средней части штифта
(см. рисунок). Считаем, что касательные
напряжения распределены по площади
среза равномерно. Составим уравнение
равновесия 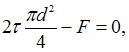 откуда
откуда ![]() Условие
прочности штифта на срез имеет
вид
Условие
прочности штифта на срез имеет
вид
![]() где
–
допускаемое касательное напряжение на
срез для штифта.
где
–
допускаемое касательное напряжение на
срез для штифта.
ЗАДАНИЕ
N 23
Тема:
Крутящий момент. Деформации и
напряжения
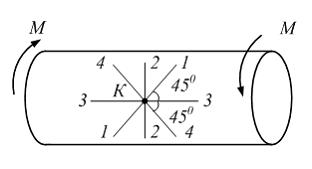 На
рисунке показан стержень, работающий
на кручение. Максимальное растягивающее
напряжение в точке К действует
в направлении …
На
рисунке показан стержень, работающий
на кручение. Максимальное растягивающее
напряжение в точке К действует
в направлении …
|
|
|
4−4 |
|
|
|
3−3 |
|
|
|
1−1 |
|
|
|
2−2 |
Решение:
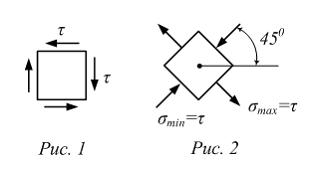 Если
в окрестности точки К двумя
поперечными, двумя продольно-осевыми
и цилиндрическим сечениями выделить
элементарный объем, то на его гранях
будут действовать касательные напряжения.
Напряженное состояние показано на
рисунке 1 через плоский элемент. При
повороте на угол
Если
в окрестности точки К двумя
поперечными, двумя продольно-осевыми
и цилиндрическим сечениями выделить
элементарный объем, то на его гранях
будут действовать касательные напряжения.
Напряженное состояние показано на
рисунке 1 через плоский элемент. При
повороте на угол ![]() касательные
напряжения на его гранях исчезают, но
появляются нормальные напряжения,
показанные на рисунке 2.
касательные
напряжения на его гранях исчезают, но
появляются нормальные напряжения,
показанные на рисунке 2.
ЗАДАНИЕ N 24 Тема: Расчет на прочность при кручении Стержень с круглым поперечным сечением, изготовленный из пластичного материала, работает на кручение. Опасным (предельным) напряжением для стержня является …
|
|
|
предел текучести при чистом сдвиге |
|
|
|
предел прочности при чистом сдвиге |
|
|
|
предел упругости при чистом сдвиге |
|
|
|
предел текучести при растяжении |
Решение:
 Напряженное
состояние материала стержня – чистый
сдвиг. На рисунке показана диаграмма
напряжений при чистом сдвиге для
пластичного материала с ярко выраженной
площадкой текучести. За опасное состояние
пластичного материала
принимается процесс текучести,
когда угол сдвига растет при постоянном
касательном напряжении, которое
называется пределом текучести материала
при чистом сдвиге
Напряженное
состояние материала стержня – чистый
сдвиг. На рисунке показана диаграмма
напряжений при чистом сдвиге для
пластичного материала с ярко выраженной
площадкой текучести. За опасное состояние
пластичного материала
принимается процесс текучести,
когда угол сдвига растет при постоянном
касательном напряжении, которое
называется пределом текучести материала
при чистом сдвиге ![]() Если
диаграмма напряжений не имеет площадки
текучести, то принято говорить об
условном пределе текучести при чистом
сдвиге. При определении условного
предела текучести вводится допуск на
остаточную деформацию после снятия
нагрузки аналогично допуску на остаточную
деформацию при определении условного
предела текучести при растяжении-сжатии
(см. учебник В. И. Феодосьева
«Сопротивление материалов», § 16. Основные
механические характеристики материалов).
Если
диаграмма напряжений не имеет площадки
текучести, то принято говорить об
условном пределе текучести при чистом
сдвиге. При определении условного
предела текучести вводится допуск на
остаточную деформацию после снятия
нагрузки аналогично допуску на остаточную
деформацию при определении условного
предела текучести при растяжении-сжатии
(см. учебник В. И. Феодосьева
«Сопротивление материалов», § 16. Основные
механические характеристики материалов).
ЗАДАНИЕ N 25 Тема: Статическая неопределимость. Степень статической неопределенности Степень статической неопределимости равна числу _____ связей, наложенных на систему.
|
|
|
дополнительных |
|
|
|
необходимых |
|
|
|
внутренних |
|
|
|
внешних |
ЗАДАНИЕ
N 26
Тема:
Расчет простейших статически неопределимых
систем
 Статически
неопределимая ферма нагружена силой F.
Модуль упругости материала Е,
площадь поперечного сечения А,
длина l всех
стержней одинаковы. Усилия N1, N2, N3 в
стержнях фермы, соответственно, равны …
Статически
неопределимая ферма нагружена силой F.
Модуль упругости материала Е,
площадь поперечного сечения А,
длина l всех
стержней одинаковы. Усилия N1, N2, N3 в
стержнях фермы, соответственно, равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Ферма
один раз статически неопределима.
Воспользуемся при решении задачи методом
сил. Получим основную систему, разрезая
стержень 3 (рис. 1а). Действие отброшенной
связи заменяем неизвестной силой ![]() (рис.
1б).
(рис.
1б).
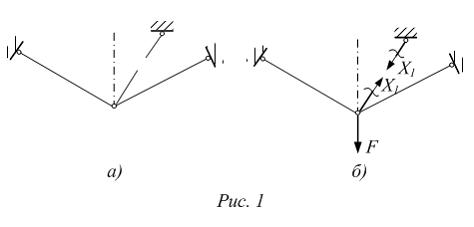 Каноническое
уравнение имеет вид
Каноническое
уравнение имеет вид
![]() Элементы
фермы работают на растяжение.
Коэффициенты
и
будут
определяться продольными силами,
возникающими в стержнях. Прикладываем
к основной системе единичную
силу
Элементы
фермы работают на растяжение.
Коэффициенты
и
будут
определяться продольными силами,
возникающими в стержнях. Прикладываем
к основной системе единичную
силу ![]() (рис. 2а).
Из
условий равновесия узла определим
продольные усилия в стержнях
(рис. 2б).
(рис. 2а).
Из
условий равновесия узла определим
продольные усилия в стержнях
(рис. 2б).
 Тогда
Тогда
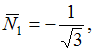
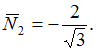 Далее
учитывая, что коэффициент
Далее
учитывая, что коэффициент
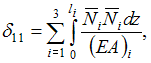 вычислим
его значение
вычислим
его значение
 Найдем
продольные усилия в стержнях основной
системы от внешней нагрузки. Прикладываем
к основной системе силу F (рис. 3а)
и, рассматривая равновесие узла
(рис. 3б),
Найдем
продольные усилия в стержнях основной
системы от внешней нагрузки. Прикладываем
к основной системе силу F (рис. 3а)
и, рассматривая равновесие узла
(рис. 3б),
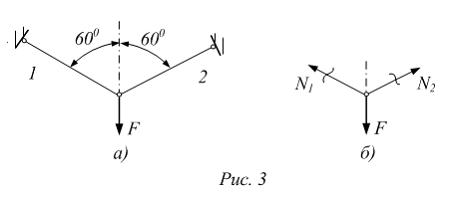 определим
определим ![]() Коэффициент
вычислим,
используя формулу
Коэффициент
вычислим,
используя формулу 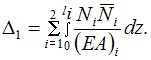 Тогда
Тогда  Решая
каноническое уравнение, получим
Решая
каноническое уравнение, получим  Знак
«плюс» показывает, что третий стержень
работает на растяжение. Для определения
продольных усилий в стержнях 1 и 2 составим
расчетную схему (рис. 4а).
К основной системе прикладываем внешнюю
силу F и
силу
Знак
«плюс» показывает, что третий стержень
работает на растяжение. Для определения
продольных усилий в стержнях 1 и 2 составим
расчетную схему (рис. 4а).
К основной системе прикладываем внешнюю
силу F и
силу 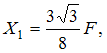 которую
рассматриваем как заданную внешнюю
силу.
которую
рассматриваем как заданную внешнюю
силу.
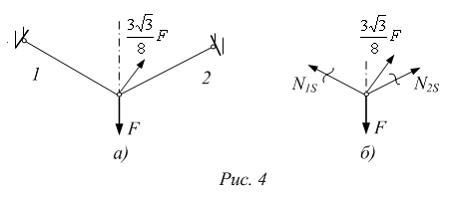 Из
условия равновесия узла (рис. 4б)
определим
Из
условия равновесия узла (рис. 4б)
определим
![]() Следовательно,
продольные усилия в стержнях имеют
значения
Следовательно,
продольные усилия в стержнях имеют
значения
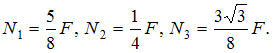
ЗАДАНИЕ N 27 Тема: Метод сил Для статически неопределимой системы один из вариантов правильно выбранной основной системы показан на рисунке …
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
Решение: Система два раза статически неопределима. При выборе основной системы необходимо отбросить две дополнительные связи. На рис. 2 отброшена одна связь, на рисунках 3 и 4 удалены три связи. Правильно выбранная основная система показана на рисунке 1.
ЗАДАНИЕ
N 28
Тема:
Определение перемещений с помощью
интегралов Мора. Правило Верещагина
Для
вычисления интегралов Мора способом
Верещагина, в случае плоского изгиба,
без учета влияния поперечных сил,
используется формула
 Произведение
Произведение ![]() –
величина …
–
величина …
|
|
|
положительная, отрицательная или равная нулю |
|
|
|
положительная |
|
|
|
положительная или равная нулю |
|
|
|
положительная или отрицательная |
Решение: Знак произведения определяется по расположению эпюр изгибающих моментов относительно их осей. Если эпюры в грузовом и единичном состояниях расположены по одну сторону от осей произведение – величина положительная. По разные стороны – – величина отрицательная. Если одна из эпюр отсутствует произведение равно нулю.
ЗАДАНИЕ
N 29
Тема:
Осевые моменты инерции. Зависимость
между моментами инерции при параллельном
переносе осей
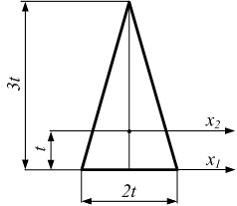 При
переходе от оси
к
оси
При
переходе от оси
к
оси ![]() осевой
момент инерции треугольника …
осевой
момент инерции треугольника …
|
|
|
уменьшится
на величину |
|
|
|
увеличится на величину |
|
|
|
не изменится |
|
|
|
увеличится
на величину |