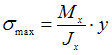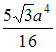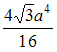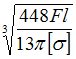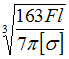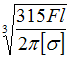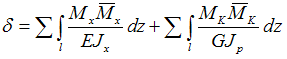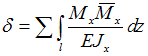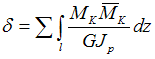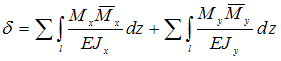Задание n 13
Тема:
Формула Эйлера для критической силы
сжатого стержня и пределы ее
применимости
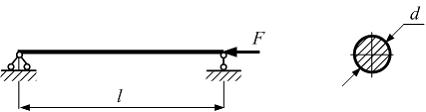 Стержень
круглого сечения диаметром d,
длиной l сжимается
силой F.
При увеличении линейных размеров l и d в
два раза значение критической силы, при
прочих равных условиях, ___________. При
решении учитывать, что напряжения в
сжатом стержне не превышают предела
пропорциональности.
Стержень
круглого сечения диаметром d,
длиной l сжимается
силой F.
При увеличении линейных размеров l и d в
два раза значение критической силы, при
прочих равных условиях, ___________. При
решении учитывать, что напряжения в
сжатом стержне не превышают предела
пропорциональности.
|
|
|
увеличится в 4 раза |
|
|
|
не изменится |
|
|
|
уменьшится в 2 раза |
|
|
|
увеличится в 8 раз |
Задание n 14
Тема:
Влияние условий закрепления концов
стержня на величину критической
силы
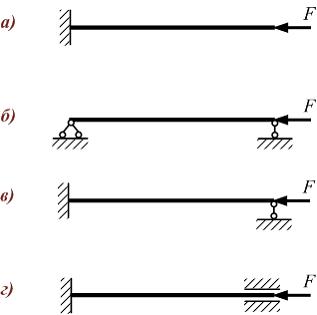 Стержни
изготовлены из одного материала, имеют
одинаковую длину, форму и размеры
поперечного сечения. Схемы закрепления
стержней, сжатых силой F,
показаны на рисунках. Наибольшее значение
гибкости имеет стержень, показанный на
рисунке …
Стержни
изготовлены из одного материала, имеют
одинаковую длину, форму и размеры
поперечного сечения. Схемы закрепления
стержней, сжатых силой F,
показаны на рисунках. Наибольшее значение
гибкости имеет стержень, показанный на
рисунке …
|
|
|
а |
|
|
|
г |
|
|
|
в |
|
|
|
б |
ЗАДАНИЕ N 15 Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня При потере устойчивости сжатого стержня изгиб стержня происходит в плоскости …
|
|
|
наименьшей жесткости |
|
|
|
наибольшей жесткости |
|
|
|
равнонаклоненной к осям симметрии |
|
|
|
расположенной в любом направлении |
ЗАДАНИЕ
N 16
Тема:
Устойчивость за пределом пропорциональности.
Расчет сжатых стержней на
устойчивость
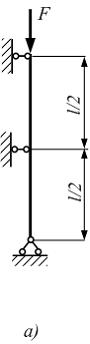
 Стержень
длиной
Стержень
длиной ![]() сжат
силой F.
Схема закрепления показана на рисунке а.
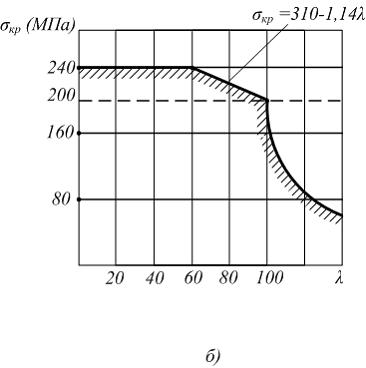
Зависимость критического напряжения
от гибкости для материала Ст. 3 приведена
на рисунке б. Поперечное сечение швеллер
№10.
Площадь поперечного сечения
сжат
силой F.
Схема закрепления показана на рисунке а.
Зависимость критического напряжения
от гибкости для материала Ст. 3 приведена
на рисунке б. Поперечное сечение швеллер
№10.
Площадь поперечного сечения ![]() радиусы
инерции
радиусы
инерции ![]()
![]() Значение
критической силы равно ____ кН.
Значение
критической силы равно ____ кН.
|
|
|
247 |
|
|
|
124 |
|
|
|
318 |
|
|
|
212 |
ЗАДАНИЕ
N 17
Тема:
Испытание конструкционных материалов
на растяжение и сжатие
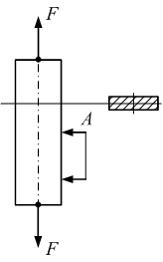 При
испытании образца на растяжение
силами F (см. рисунок)
стрелка тензометра А с
базой, равной 60 мм,
переместилась с деления 5 на деление 9.
Цена деления шкалы тензометра 0,001 мм.
Модуль упругости материала
образца
При
испытании образца на растяжение
силами F (см. рисунок)
стрелка тензометра А с
базой, равной 60 мм,
переместилась с деления 5 на деление 9.
Цена деления шкалы тензометра 0,001 мм.
Модуль упругости материала
образца ![]() Напряжение
в крайнем правом слое равно ____ МПа.
Напряжение
в крайнем правом слое равно ____ МПа.
|
|
|
13,3 |
|
|
|
30 |
|
|
|
46,7 |
|
|
|
22 |
Решение:
Напряжение
определим по закону Гука.
![]()
ЗАДАНИЕ N 18 Тема: Механические свойства и механические характеристики материалов Для хрупких материалов за опасное (предельное) напряжение принимается предел …
|
|
|
прочности |
|
|
|
пропорциональности |
|
|
|
текучести |
|
|
|
выносливости |
ЗАДАНИЕ
N 19
Тема:
Расчеты стержней на прочность и
жесткость
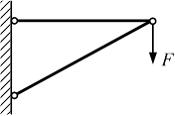 Стержни
фермы (см. рисунок) изготовлены из
пластичного материала с одинаковыми
пределами текучести на растяжение и
сжатие. Условие прочности фермы, из
расчета по допускаемым напряжениям,
имеет вид …
Стержни
фермы (см. рисунок) изготовлены из
пластичного материала с одинаковыми
пределами текучести на растяжение и
сжатие. Условие прочности фермы, из
расчета по допускаемым напряжениям,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
В
начале отметим, что пределы текучести
пластичного материала при растяжении
и сжатии одинаковы, то есть ![]() В
методе расчета по допускаемым напряжениям
за опасное состояние фермы следует
принять такое состояние, при котором в
наиболее напряженном стержне возникают
пластические (необратимые) деформации.
Пластические деформации появляются
тогда, когда напряжение достигает
величины предела текучести. Поэтому
условие прочности для фермы имеет
вид
В
методе расчета по допускаемым напряжениям
за опасное состояние фермы следует
принять такое состояние, при котором в
наиболее напряженном стержне возникают
пластические (необратимые) деформации.
Пластические деформации появляются
тогда, когда напряжение достигает
величины предела текучести. Поэтому
условие прочности для фермы имеет
вид ![]() где:
где: ![]() –
максимальное напряжение в ферме, взятое
по абсолютной величине,
–
максимальное напряжение в ферме, взятое
по абсолютной величине, 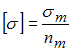 –
допускаемое напряжение,
–
допускаемое напряжение, ![]() –
предел текучести для материала
стержней,
–
предел текучести для материала
стержней, ![]() –
коэффициент запаса прочности.
–
коэффициент запаса прочности.
ЗАДАНИЕ
N 20
Тема:
Продольная сила. Напряжения и
деформации
 Значение
продольной силы в сечении С-С равно …
Значение
продольной силы в сечении С-С равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
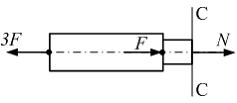 Сечением
С-С делим стержень на две части. Для того
чтобы определить продольную силу в
сечении, следует рассмотреть равновесие
одной из частей. Рассмотрим, например,
равновесие левой части (см. рисунок).
Продольную силу N направляем
от сечения, полагая, что она растягивает
материал участка. Уравнение равновесия
имеет вид
Сечением
С-С делим стержень на две части. Для того
чтобы определить продольную силу в
сечении, следует рассмотреть равновесие
одной из частей. Рассмотрим, например,
равновесие левой части (см. рисунок).
Продольную силу N направляем
от сечения, полагая, что она растягивает
материал участка. Уравнение равновесия
имеет вид ![]() откуда
откуда ![]()
ЗАДАНИЕ N 21 Тема: Расчет балок на прочность Консольная балка длиной l нагружена моментом М. Значение допускаемого нормального напряжения известно. Из расчета на прочность по нормальные напряжениям минимально допустимое значение диаметра поперечного сечения d равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 22 Тема: Напряжения в поперечном сечении стержня при плоском изгибе При определении наибольшего нормального напряжения в поперечном сечении балки, при плоском изгибе, используют формулу …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Наибольшее
нормальное напряжение, при плоском
изгибе, возникает в точках поперечного
сечения балки наиболее удаленных от
нейтральной линии и определяется по
формуле 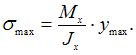 Отношение
Отношение ![]() называется
моментом сопротивления при изгибе и
обозначается
называется
моментом сопротивления при изгибе и
обозначается ![]()
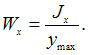 Поэтому
Поэтому 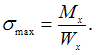
ЗАДАНИЕ
N 23
Тема:
Поперечная сила, изгибающий момент и
их эпюры
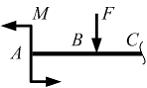 На
схеме показана отсеченная часть балки
и нагрузка, действующая на
нее. Неверным является
утверждение, что изгибающий момент …
На
схеме показана отсеченная часть балки
и нагрузка, действующая на
нее. Неверным является
утверждение, что изгибающий момент …
|
|
|
в сечении В изменяется скачком |
|
|
|
в сечении А изменяется скачком |
|
|
|
на участке АВ постоянный |
|
|
|
на участке ВС переменный |
Решение: В сечении, где к балке приложен момент, на эпюре изгибающих моментов должен быть скачок на величину этого момента. В сечении В приложена сосредоточенная сила. Поэтому неправельным будет ответ, что изгибающий момент в сечении В изменяется скачком.
ЗАДАНИЕ N 24 Тема: Перемещения при изгибе. Расчет балок на жесткость Однопролетная балка длиной l, высотой h нагружена равномерно распределенной нагрузкой. Радиус кривизны нейтрального слоя балки в середине пролета равен . Жесткость поперечного сечения на изгиб по всей длине постоянна. Максимальное нормальное напряжение в балке равно … (Влияние поперечной силы на изменение кривизны не учитывать).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: При изгибе балки кривизна нейтрального слоя связана с изгибающим моментом и жесткостью поперечного сечения на изгиб соотношением Следовательно, в середине пролета, в котором возникает максимальный изгибающий момент, имеем Максимальное нормальное напряжение найдем по формуле Учитывая, что , получим
ЗАДАНИЕ
N 25
Тема:
Моменты инерции простых и сложных
сечений
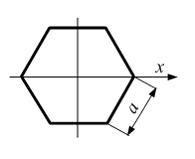 Момент
инерции правильного шестиугольника с
размером стороны а относительно
оси x равен …
Момент
инерции правильного шестиугольника с
размером стороны а относительно
оси x равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 26
Тема:
Статические моменты. Центр тяжести
плоской фигуры
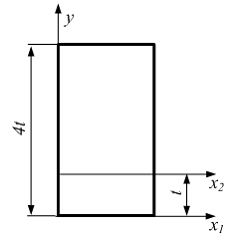 При
перемещении координатной оси из
положения
При
перемещении координатной оси из
положения ![]() в
положение
в
положение ![]() статический
момент прямоугольника …
статический
момент прямоугольника …
|
|
|
уменьшается в два раза |
|
|
|
увеличивается в два раза |
|
|
|
уменьшается в четыре раза |
|
|
|
увеличивается в полтора раза |
Решение: Статический момент относительно оси x есть произведение площади на координату ее центра тяжести по оси y. При перемещении оси из положения в положение координата центра тяжести прямоугольника, а значит и его статический момент, уменьшаются в два раза.
ЗАДАНИЕ
N 27
Тема:
Осевые моменты инерции. Зависимость
между моментами инерции при параллельном
переносе осей
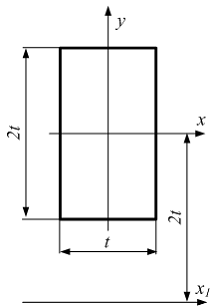 Ось x проходит
через центр тяжести прямоугольника.
Осевой момент инерции прямоугольника
относительно оси
равен …
Ось x проходит
через центр тяжести прямоугольника.
Осевой момент инерции прямоугольника
относительно оси
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
определения осевого момента инерции
прямоугольника относительно
оси
используем
формулу параллельного переноса
ЗАДАНИЕ N 28 Тема: Главные оси и главные моменты инерциим Главными центральными осями называются …
|
|
|
главные оси, проходящие через центр тяжести фигуры |
|
|
|
оси, в системе которых касательные напряжения равны нулю |
|
|
|
главные оси деформированного состояния |
|
|
|
главные оси, одна из которых является центральной |
ЗАДАНИЕ N 29 Тема: Основные понятия, определения, допущения и принципы Свойство материала сохранять некоторую часть деформации после снятия нагрузки называется …
|
|
|
пластичностью |
|
|
|
упругостью |
|
|
|
жесткостью |
|
|
|
твердостью |
ЗАДАНИЕ N 30 Тема: Модели прочностной надежности Материал полностью заполняет объем тела и имеет беспустотную, бездефектную структуру. Данная гипотеза называется гипотезой …
|
|
|
сплошной среды |
|
|
|
однородности |
|
|
|
изотропности |
|
|
|
абсолютной упругости |
Решение: Реальный материал имеет множество внутренних дефектов (трещины, газовые пузыри, инородные включения), которые невозможно учесть в расчетах. Невозможно учесть в расчетах и особенности кристаллического строения металлов. Поэтому в курсе сопротивления материалов материал рассматривается как сплошная среда.
ЗАДАНИЕ N 31 Тема: Внутренние силы и напряжения При растяжении-сжатии прямого стержня дополнительные внутренние силы, действующие в поперечном сечении, образуют …
|
|
|
пространственную систему параллельных сил перпендикулярных к плоскости сечения |
|
|
|
плоскую систему сходящихся сил |
|
|
|
плоскую систему параллельных сил |
|
|
|
пространственную систему сходящихся сил |
Решение: При растяжении-сжатии прямого стержня дополнительные внутренние силы, действующие в поперечном сечении, образуют пространственную систему параллельных сил перпендикулярных к плоскости сечения.
ЗАДАНИЕ N 32 Тема: Перемещение и деформация Угловая деформация − это …
|
|
|
изменение угла между двумя взаимно перпендикулярными до деформации малыми отрезками, проходящими через данную точку. |
|
|
|
угол поворота прямого отрезка малой длины в пространстве |
|
|
|
сумма углов
поворота прямого отрезка малой длины
в координатных плоскостях |
|
|
|
угол поворота тела в пространстве как жесткого целого |
Решение:
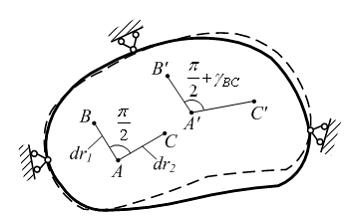 Рассмотрим
два взаимно перпендикулярных до
деформации малых отрезка
Рассмотрим
два взаимно перпендикулярных до
деформации малых отрезка ![]() и
и ![]() (см.
рисунок). В процессе деформации тела
точки А, В, С,
перемещаются в положения А', В', С'.
Прямой угол между направлениями АВ и АС изменяется
на величину
(см.
рисунок). В процессе деформации тела
точки А, В, С,
перемещаются в положения А', В', С'.
Прямой угол между направлениями АВ и АС изменяется
на величину ![]() Изменение
прямого угла между направлениями АВ и АС называется
угловой деформацией или углом сдвига
между этими направлениями. Если
рассматривать различные пары взаимно
перпендикулярных до деформации
направлений, проходящих через точку А,
то угловые деформации между ними в общем
случае будут различными.
Изменение
прямого угла между направлениями АВ и АС называется
угловой деформацией или углом сдвига
между этими направлениями. Если
рассматривать различные пары взаимно
перпендикулярных до деформации
направлений, проходящих через точку А,
то угловые деформации между ними в общем
случае будут различными.
(5)
ЗАДАНИЕ
N 1
Тема:
Оценка прочности материала при сложном
напряженном состоянии. Теории
прочности
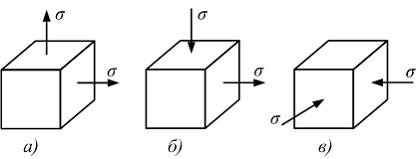 Согласно
теории наибольших касательных напряжений
(третья теория прочности), самое опасное
напряженное состояние показано на
рисунке …
Согласно
теории наибольших касательных напряжений
(третья теория прочности), самое опасное
напряженное состояние показано на
рисунке …
|
|
|
б |
|
|
|
в |
|
|
|
а |
|
|
|
все три напряженные состояния равноопасны |
ЗАДАНИЕ
N 2
Тема:
Виды напряженного состояния
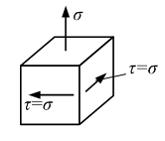 Напряженное
состояние элементарного объема
является – …
Напряженное
состояние элементарного объема
является – …
|
|
|
объемное |
|
|
|
плоское |
|
|
|
линейное (одноосное растяжение) |
|
|
|
линейное (одноосное сжатие) |
Решение:
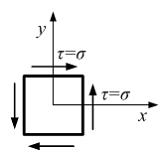 Верхняя
грань элементарного объема является
главной площадкой, поэтому одно главное
напряжение равно
Два
других главных напряжения вычисляем
по формуле
Верхняя
грань элементарного объема является
главной площадкой, поэтому одно главное
напряжение равно
Два
других главных напряжения вычисляем
по формуле 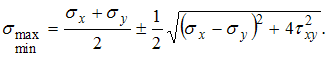 В
данном случае (см. рис.)
В
данном случае (см. рис.) ![]()
![]() Подставляя
в формулу, получаем
Подставляя
в формулу, получаем ![]() Присваивая
главным напряжениям соответствующие
индексы, получаем
Присваивая
главным напряжениям соответствующие
индексы, получаем ![]() Напряженное
состояние − объемное.
Напряженное
состояние − объемное.
ЗАДАНИЕ
N 3
Тема:
Деформированное состояние в точке.
Связь между деформациями и
напряжениями
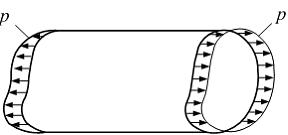 Стержень
растянут усилиями, равномерно
распределенными по его торцам
с интенсивностью р. Модуль
упругости Е и
коэффициент Пуассона
материала
стержня известны. Относительное изменение
объема стержня равно …
Стержень
растянут усилиями, равномерно
распределенными по его торцам
с интенсивностью р. Модуль
упругости Е и
коэффициент Пуассона
материала
стержня известны. Относительное изменение
объема стержня равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 4 Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) Главными осями напряженного состояния называются …
|
|
|
три взаимно перпендикулярные оси, в системе которых касательные напряжения на гранях элементарного объема равны нулю |
|
|
|
оси, совпадающие с ребрами элементарного объема |
|
|
|
оси, совпадающие
с векторами напряжений |
|
|
|
три взаимно перпендикулярные оси, в системе которых нормальные напряжения на гранях элементарного объема равны нулю |
Решение:
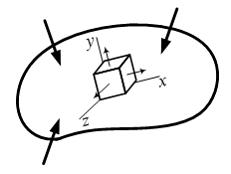 На
рисунке показан элементарный объем,
выделенный в окрестности произвольной
точки нагруженного тела. Если при данной
ориентации элементарного объема
касательные напряжения на его гранях
равны нулю, то оси x, y, z называются
главными осями напряженного состояния.
При переходе от одной точки к другой
направления главных осей в общем случае
изменяются.
На
рисунке показан элементарный объем,
выделенный в окрестности произвольной
точки нагруженного тела. Если при данной
ориентации элементарного объема
касательные напряжения на его гранях
равны нулю, то оси x, y, z называются
главными осями напряженного состояния.
При переходе от одной точки к другой
направления главных осей в общем случае
изменяются.
ЗАДАНИЕ
N 5
Тема:
Расчет простейших статически неопределимых
систем
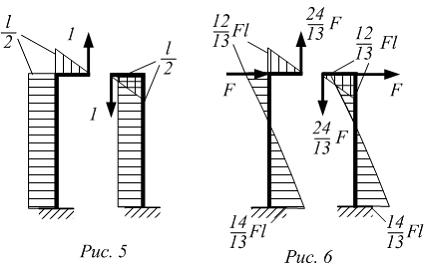
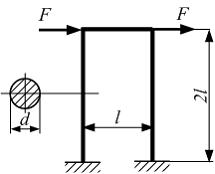 На
рисунке показана рама с постоянным по
контуру круглым поперечным сечением,
нагруженная силами F.
Известны величины: F, l, E,
.
Из расчета на прочность по допускаемым
напряжениям минимально допустимое
значение диаметра равно …
На
рисунке показана рама с постоянным по
контуру круглым поперечным сечением,
нагруженная силами F.
Известны величины: F, l, E,
.
Из расчета на прочность по допускаемым
напряжениям минимально допустимое
значение диаметра равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
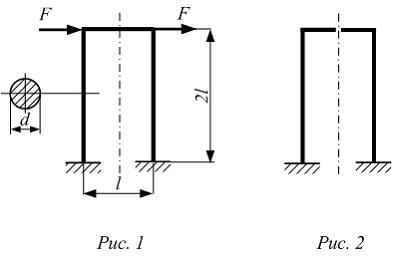
 Рама
(рис. 1) статически неопределима. Для
раскрытия статической неопределимости
используем метод сил. На рисунках 2 и 3
показаны основная и эквивалентная
системы. Рама геометрически симметрична
и нагружена кососимметричной нагрузкой.
Следовательно, в поперечном сечении,
совпадающим с осью симметрии, нулю не
равняется только кососимметричный
внутренниый силовой фактор, поперечная
сила
(рис. 3).
Каноническое уравнение метода сил имеет
вид
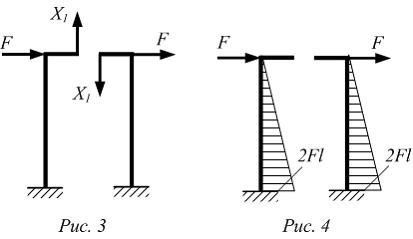
Определяем
коэффициенты канонического уравнение,
используя для вычисления интегралов
Мора способ Верещагина. Для этого строим
эпюры изгибающих моментов в грузовом
и единичном состояниях основной системы
(рис. 4, 5) и перемножаем их.
Рама
(рис. 1) статически неопределима. Для
раскрытия статической неопределимости
используем метод сил. На рисунках 2 и 3
показаны основная и эквивалентная
системы. Рама геометрически симметрична
и нагружена кососимметричной нагрузкой.
Следовательно, в поперечном сечении,
совпадающим с осью симметрии, нулю не
равняется только кососимметричный
внутренниый силовой фактор, поперечная
сила
(рис. 3).
Каноническое уравнение метода сил имеет
вид
Определяем
коэффициенты канонического уравнение,
используя для вычисления интегралов
Мора способ Верещагина. Для этого строим
эпюры изгибающих моментов в грузовом
и единичном состояниях основной системы
(рис. 4, 5) и перемножаем их.

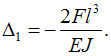 Подставляя
значения
и
в
каноническое уравнение,
получаем
Подставляя
значения
и
в
каноническое уравнение,
получаем ![]() Откуда
Откуда ![]() Подставляем
значение
в
эквивалентную систему и строим эпюру
изгибающего момента для заданной рамы
(рис. 6).
Условие прочности имеет
вид
Подставляем
значение
в
эквивалентную систему и строим эпюру
изгибающего момента для заданной рамы
(рис. 6).
Условие прочности имеет
вид
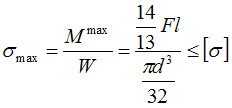 .
Откуда
.
Откуда 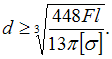
ЗАДАНИЕ
N 6
Тема:
Определение перемещений с помощью
интегралов Мора. Правило Верещагина
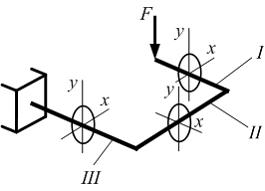 Формула
интеграла Мора, не учитывающая влияние
поперечной силы, для данной расчетной
схемы имеет вид …
Формула
интеграла Мора, не учитывающая влияние
поперечной силы, для данной расчетной
схемы имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ
N 7
Тема:
Статическая неопределимость. Степень
статической неопределенности
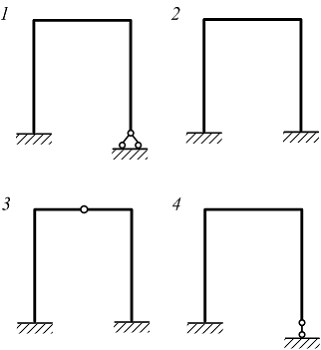 Один
раз статически неопределимая рама
показана на рисунке …
Один
раз статически неопределимая рама
показана на рисунке …
|
|
|
4 |
|
|
|
2 |
|
|
|
3 |
|
|
|
1 |
Решение:
Определим
последовательно степень статической
неопределимости представленных плоских
рам по формуле ![]() ,
где k –
число замкнутых контуров;
ш –
число одиночных шарниров.
1. Рама
имеет два контура и четыре одиночных
шарнира, то есть два раза статически
неопределима.
2. Рама имеет один
контур, а одиночные шарниры отсутствуют,
то есть три раза статически неопределима.
3.
Рама имеет одиночный шарнир и один
контур, то есть два раза статически
неопределима.
4. Рама содержит один
контур и два одиночных шарнира, то есть
один раз статически неопределима.
Следовательно,
на рисунке 4 показана один раз статически
неопределимая рама.
,
где k –
число замкнутых контуров;
ш –
число одиночных шарниров.
1. Рама
имеет два контура и четыре одиночных
шарнира, то есть два раза статически
неопределима.
2. Рама имеет один
контур, а одиночные шарниры отсутствуют,
то есть три раза статически неопределима.
3.
Рама имеет одиночный шарнир и один
контур, то есть два раза статически
неопределима.
4. Рама содержит один
контур и два одиночных шарнира, то есть
один раз статически неопределима.
Следовательно,
на рисунке 4 показана один раз статически
неопределимая рама.
ЗАДАНИЕ N 8 Тема: Метод сил Система канонических уравнений метода сил имеет вид Левая часть каждого уравнения это перемещение в направлении i-ой отброшенной связи, вызванное …
|
|
|
реакциями отброшенных связей и внешней нагрузкой |
|
|
|
внешней нагрузкой |
|
|
|
реакциями отброшенных связей |
|
|
|
силой |
Решение: Левая часть каждого уравнения (в системе канонических уравнений метода сил) это перемещение в направлении i-ой отброшенной связи, вызванное реакциями связей и внешней нагрузкой.
ЗАДАНИЕ N 9 Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Признаком потери устойчивости сжатого стержня при статическом нагружении является …
|
|
|
внезапная смена прямолинейной формы равновесия на криволинейную |
|
|
|
резкое уменьшение длины сжатого стержня |
|
|
|
увеличение напряжений в сжатом стержне до предела текучести |
|
|
|
увеличение напряжений в сжатом стержне до предела прочности |
ЗАДАНИЕ
N 10
Тема:
Влияние условий закрепления концов
стержня на величину критической
силы
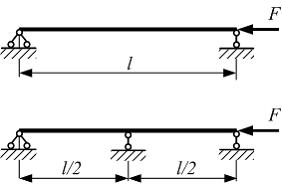 Шарнирно-опертый
по концам стержень длиной l сжимается
силой F.
При постановке в середине пролета
промежуточной опоры значение гибкости …
Шарнирно-опертый
по концам стержень длиной l сжимается
силой F.
При постановке в середине пролета
промежуточной опоры значение гибкости …
|
|
|
уменьшится в 2 раза |
|
|
|
не изменится |
|
|
|
увеличится в 2 раза |
|
|
|
уменьшится в 4 раза |
ЗАДАНИЕ
N 11
Тема:
Формула Эйлера для критической силы
сжатого стержня и пределы ее
применимости
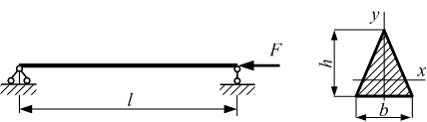 Стержень
длиной l=2м нагружен
силой F.
Поперечное сечение – равнобедренный
треугольник шириной основания
Стержень
длиной l=2м нагружен
силой F.
Поперечное сечение – равнобедренный
треугольник шириной основания ![]() и
высотой
и
высотой ![]() Модуль
упругости материала стержня
Модуль
упругости материала стержня ![]() предел
пропорциональности
предел
пропорциональности ![]() Схема
закрепления стержня показана на рисунке.
Значение критической силы равно _____ кН.
Принять
Схема
закрепления стержня показана на рисунке.
Значение критической силы равно _____ кН.
Принять ![]()
|
|
|
40 |
|
|
|
20 |
|
|
|
30 |
|
|
|
80 |
Решение:
При
заданных характеристиках материала
определим наименьшее значение гибкости,
при которой можно пользоваться, для
определения критической силы сжатого
стержня, формулой Эйлера
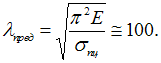 Определим
гибкость стержня по формуле
Определим
гибкость стержня по формуле
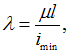 где
где 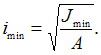 При
заданных условиях опирания концов
стержня
При
заданных условиях опирания концов
стержня ![]() Минимальный
радиус инерции сечения
Минимальный
радиус инерции сечения
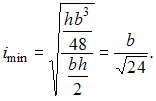 После
вычислений получим
После
вычислений получим
![]() Следовательно,
для определения критической силы
необходимо использовать формулу
Эйлера
Следовательно,
для определения критической силы
необходимо использовать формулу
Эйлера
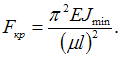 Подставив
числовые значения найдем
Подставив
числовые значения найдем
![]()
ЗАДАНИЕ
N 12
Тема:
Устойчивость за пределом пропорциональности.
Расчет сжатых стержней на устойчивость
При
расчетах сжатых стержней на устойчивость
коэффициент уменьшения основного
допускаемого напряжения ![]() определяют
в зависимости от марки материала и
________ стержня.
определяют
в зависимости от марки материала и
________ стержня.
|
|
|
гибкости |
|
|
|
жесткости |
|
|
|
площади сечения |
|
|
|
длины |
ЗАДАНИЕ N 13 Тема: Напряжения в поперечном сечении стержня при плоском изгибе Эпюра распределения нормальных напряжений при чистом изгибе балки, показанной на схеме, имеет вид …
|
|
|
b |
|
|
|
a |
|
|
|
c |
|
|
|
d |
Решение:
Для
определения нормального напряжения
в точках поперечного сечения балки при
чистом изгибе используют
формулу 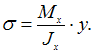 Зависимость
Зависимость ![]() от y линейная.
Максимальные
напряжения возникают в точках, наиболее
удаленных от нейтральной линии.
При
заданной схеме нагружения балки верхние
слои испытывают деформацию растяжения,
а нижние сжатия. Следовательно, эпюра
распределения нормальных напряжений,
для данного варианта нагружения, показана
на схеме b.
от y линейная.
Максимальные
напряжения возникают в точках, наиболее
удаленных от нейтральной линии.
При
заданной схеме нагружения балки верхние
слои испытывают деформацию растяжения,
а нижние сжатия. Следовательно, эпюра
распределения нормальных напряжений,
для данного варианта нагружения, показана
на схеме b.
ЗАДАНИЕ
N 14
Тема:
Расчет балок на прочность
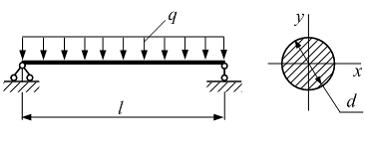 Однопролетная
деревянная балка длиной
Однопролетная
деревянная балка длиной ![]() нагружена
равномерно распределенной нагрузкой
интенсивности q.
Диаметр поперечного сечения
нагружена
равномерно распределенной нагрузкой
интенсивности q.
Диаметр поперечного сечения ![]() Значение
допускаемого нормального напряжения
Значение
допускаемого нормального напряжения ![]() Из
расчета на прочность по нормальным
напряжениям максимально допустимое
значение интенсивности нагрузки q равно ____
Из
расчета на прочность по нормальным
напряжениям максимально допустимое
значение интенсивности нагрузки q равно ____ ![]()
|
|
|
5,88 |
|
|
|
5,58 |
|
|
|
6,24 |
|
|
|
4,68 |
ЗАДАНИЕ
N 15
Тема:
Перемещения при изгибе. Расчет балок
на жесткость
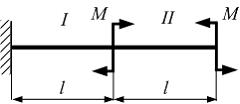
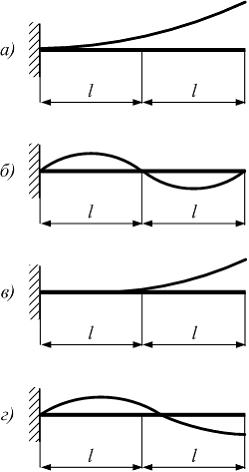 Консоль
нагружена внешними моментами. Примерный
вид изогнутой оси балки показан на
схеме …
Консоль
нагружена внешними моментами. Примерный
вид изогнутой оси балки показан на
схеме …
|
|
|
в |
|
|
|
а |
|
|
|
б |
|
|
|
г |
Решение: Балка имеет два силовых участка. На первом участке изгибающий момент равен. Поэтому на первом участке балка останется прямой. Второй участок испытывает деформацию чистый изгиб. Радиус кривизны оси балки во всех сечениях будет одинаков. Нижние слои балки работают на растяжение, верхние – на сжатие. Поэтому, примерный вид изогнуто оси балки соответствует схеме «в».
ЗАДАНИЕ N 16 Тема: Поперечная сила, изгибающий момент и их эпюры Однопролетная балка ВС длиной нагружена силой и равномерно распределенной нагрузкой интенсивности q. Максимальные значения изгибающего момента и поперечной силы по абсолютной величине соответственно равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Заменяем
действие отброшенных на балку связей
реакциями: ![]()
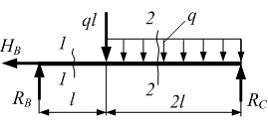 Используя
уравнения статики, найдем:
Используя
уравнения статики, найдем: ![]() Балка
имеет два участка. Для определения
внутренних силовых факторов на каждом
участке воспользуемся методом сечений.
Рассекаем балку на левом участке
произвольным сечением 1–1 и отбросим
правую часть.
Рассмотрим равновесие
левой оставшейся части. Действие
отброшенной правой части заменяем на
левую поперечной силой
Балка
имеет два участка. Для определения
внутренних силовых факторов на каждом
участке воспользуемся методом сечений.
Рассекаем балку на левом участке
произвольным сечением 1–1 и отбросим
правую часть.
Рассмотрим равновесие
левой оставшейся части. Действие
отброшенной правой части заменяем на
левую поперечной силой ![]() и
изгибающим моментом
и
изгибающим моментом ![]() (Напоминаем,
что при плоском поперечном изгибе в
поперечном сечении балки возникают два
внутренних силовых фактора: поперечная
сила Q и
изгибающий момент М).
(Напоминаем,
что при плоском поперечном изгибе в
поперечном сечении балки возникают два
внутренних силовых фактора: поперечная
сила Q и
изгибающий момент М).
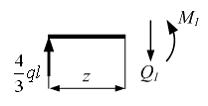 Переменная z отсчитывается
от крайнего левого сечения и изменяется
в пределах
Переменная z отсчитывается
от крайнего левого сечения и изменяется
в пределах ![]() .
Из уравнений равновесия получим
.
Из уравнений равновесия получим ![]() Следовательно,
поперечная сила по длине первого участка
постоянна, а изгибающий момент меняется
по линейному закону. Вычислим значения
Следовательно,
поперечная сила по длине первого участка
постоянна, а изгибающий момент меняется
по линейному закону. Вычислим значения![]() в
начале и в конце участка
в
начале и в конце участка ![]()
![]() Затем
рассекаем балку произвольным сечением
2–2 в пределах второго участка и рассмотрим
равновесие правой
части.
Затем
рассекаем балку произвольным сечением
2–2 в пределах второго участка и рассмотрим
равновесие правой
части.
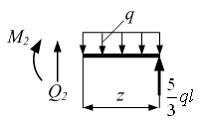 Переменная z отсчитывается
от крайнего правого сечения и меняется
в пределах
Переменная z отсчитывается
от крайнего правого сечения и меняется
в пределах ![]() Из
условий равновесия правой части
найдем
Из
условий равновесия правой части
найдем
![]()
![]() Поперечная
сила по длине второго участка меняется
по линейному закону, а изгибающий момент
по закону квадратной параболы. Найдем
значения
Поперечная
сила по длине второго участка меняется
по линейному закону, а изгибающий момент
по закону квадратной параболы. Найдем
значения ![]() и
и ![]() в
начале и конце участка:
в
начале и конце участка:
![]()
![]() Из
полученных значений для
следует,
что в некотором сечении второго участка
поперечная сила
Из
полученных значений для
следует,
что в некотором сечении второго участка
поперечная сила ![]() Положение
данного сечения ( координату z)
определим из уравнения
Положение
данного сечения ( координату z)
определим из уравнения ![]() ,
отсюда
,
отсюда ![]() Выражение
для изгибающего момента содержит
переменную во второй степени. Поэтому
исследуем функцию
на
аналитический экстремум
Выражение
для изгибающего момента содержит
переменную во второй степени. Поэтому
исследуем функцию
на
аналитический экстремум
![]() Следовательно,
в сечении
Следовательно,
в сечении ![]() (в
данном сечении поперечная сила равна
нулю) изгибающий момент принимает
экстремальное значение
(в
данном сечении поперечная сила равна
нулю) изгибающий момент принимает
экстремальное значение 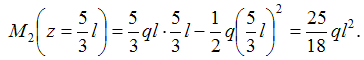 Сравнивая
полученные значения поперечных сил и
изгибающих моментов, делаем вывод, что
Сравнивая
полученные значения поперечных сил и
изгибающих моментов, делаем вывод, что 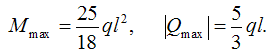
ЗАДАНИЕ N 17 Тема: Моменты инерции простых и сложных сечений Момент инерции равнобедренного треугольника относительно оси x, проходящей через центр тяжести параллельно основанию, равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 18 Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей Осевой момент инерции треугольника относительно оси проходящей через его центр тяжести параллельно основанию определяется по формуле …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|