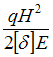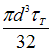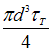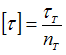Задание n 7

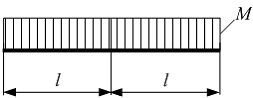
Тема: Поперечная сила, изгибающий момент и их эпюры Балка длиной l нагружена моментом М. Поперечная сила по длине балки …

			постоянна
			равна нулю
			меняется по линейному закону
			меняется по закону квадратной параболы

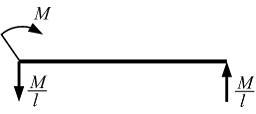
Решение: Используя уравнения статики определим реакции в опорах. Затем рассекаем балку поперечным сечением на расстоянии z от правой опоры   Из условия равновесия правой части найдем   Поперечная сила   от переменной z не зависит. Следовательно, по длине балки поперечная сила постоянна.

 ЗАДАНИЕ N 8  Тема: Перемещения при изгибе. Расчет балок на жесткость Консольная балка длиной   нагружена силой F и моментом   Размеры поперечного сечения по длине балки не меняются. Модуль упругости материала Е. Форма изогнутой оси балки на первом участке описывается кривой _______ порядка, а на втором _______ порядка.

			I – третьего, II – второго
			I –второго, II – второго
			I – третьего, II – третьего
			I –второго, II – третьего

  ЗАДАНИЕ N 9  Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость Поперечное сечение стержня состоит из четырех равнобоких уголков. Наиболее рациональная форма, с позиции устойчивости, показана на схеме …

			в
			а
			г
			б

Решение: Площади поперечного сечения для всех вариантов форм одинаковы. При проектировании формы поперечного сечения стержня, с позиции устойчивости, необходимо при одинаковой площади стремиться к получению наибольших центральных моментов инерции. Вместе с тем надо стремиться к тому, чтобы все центральные моменты инерции сечения были равны. Таким критериям отвечает форма на схеме «в».

 ЗАДАНИЕ N 10  Тема: Влияние условий закрепления концов стержня на величину критической силы Схема закрепления стержня длиной l показана на рисунке. При удалении промежуточной опоры в середине пролета значение критического напряжения … При решении учитывать, что напряжения в сжатых стержнях не превышают предел пропорциональности.

			уменьшится в 4 раза
			не изменится
			увеличится в 4 раза
			уменьшится в 2 раза

  ЗАДАНИЕ N 11  Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Стержень квадратного сечения со стороной b сжимается силой F. При замене квадратного сечения на прямоугольное шириной   и высотой   при прочих равных условиях, гибкость стержня …

			увеличится в 2 раза
			не изменится
			уменьшится в 2 раза
			увеличится в 4 раза

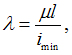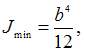
Решение: Гибкость стержня определяется по формуле где минимальный радиус инерции сечения При прочих равных условиях, гибкость зависит от минимального радиуса инерции. Для квадратного сечения     Для прямоугольного сечения с размерами   и   имеем     Следовательно, минимальный радиус инерции уменьшается в два раза, а гибкость, соответственно, увеличивается в два раза.

  ЗАДАНИЕ N 12  Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Наименьшему значению критической силы соответствует форма потери устойчивости, показанная на рисунке …

			а
			г
			б
			в

Решение: Стержень, жестко защемленный одним концом и нагруженный осевой сжимающей силой на другом, находится в таких же условиях, как стержень шарнирно-закрепленный по обоим концам. Поэтому, наименьшему значению критической силы соответствует форма потери устойчивости, показанная на рисунке «а».

  ЗАДАНИЕ N 13  Тема: Продольная сила. Напряжения и деформации Отношение значений продольных сил в сечениях С-С и К-К (см. рисунок) равно …

			1
			–1

Решение: Оба сечения принадлежат одному грузовому участку. Величина продольной силы не зависит от площади поперечного сечения. Поэтому отношение 

  ЗАДАНИЕ N 14  Тема: Механические свойства и механические характеристики материалов 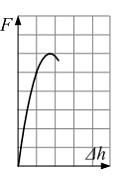На рисунке показана диаграмма сжатия чугунного образца диаметром 15 мм. Масштаб нагрузки – 1 деление – 0,02 МН. Предел прочности чугуна при сжатии равен ____ МПа.

			678
			565
			700
			860

Решение: Предел прочности чугуна при сжатии определим по формуле   где  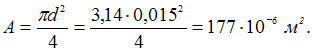  Подставляя числовые значения, получаем 

 ЗАДАНИЕ N 15  Тема: Расчеты стержней на прочность и жесткость 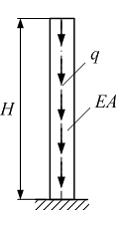На рисунке показан стержень, нагруженный равномерно распределенной нагрузкой с интенсивностью q. Величины Н, Е, q известны.  – допускаемое перемещение верхнего поперечного сечения стержня задано. Минимально допустимая площадь поперечного сечения при этом равна …

  ЗАДАНИЕ N 16  Тема: Испытание конструкционных материалов на растяжение и сжатие 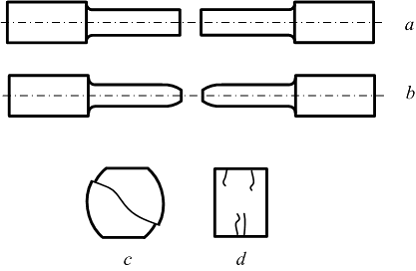Характер разрушения образца из хрупкого материала при растяжении показан на рисунке …

			а
			b
			c
			d

Решение: Образец из хрупкого материала при растяжении разрушается без образования шейки, что и показано на рисунке «а».

 ЗАДАНИЕ N 17  Тема: Виды напряженного состояния 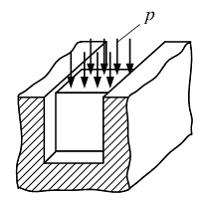Стальной кубик вставлен без зазора в жесткую обойму (см. рис.). На верхнюю грань кубика действует равномерно распределенное давление интенсивности р. Поверхности кубика и обоймы абсолютно гладкие. Напряженное состояние кубика показано на рисунке …

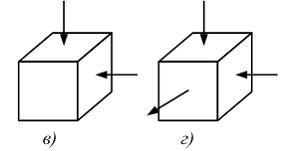
			в
			г
			б
			а

  ЗАДАНИЕ N 18  Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями На рисунке показано напряженное состояние в точке. Модуль упругости  , коэффициент Пуассона   Главные линейные деформации   соответственно равны …

Решение: Фронтальная грань элементарного параллелепипеда является главной площадкой с главным напряжением равным нулю. Напряженное состояние чистый сдвиг. Главные напряжения при чистом сдвиге:   Присваивая главным напряжениям индексы, имеем:  Главные деформации определим, используя формулы обобщенного закона Гука. Подставляя числовые значения, получаем:

 ЗАДАНИЕ N 19  Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) Число компонент напряженного состояния, полностью определяющих напряженное состояние в точке, равно …

			шести
			девяти
			четырем
			двум

  ЗАДАНИЕ N 20  Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности На рисунке показано напряженное состояние в точке. Материал хрупкий с пределом прочности на растяжение   и пределом прочности на сжатие   Коэффициент Пуассона  Величина эквивалентного напряжения равна _____ МПа, прочность материала ______. Использовать теорию наибольших линейных деформаций удлинения.

			4,34, не обеспечена
			4,34, обеспечена
			6, не обеспечена
			3,66, обеспечена

Решение: Главные напряжения:  Эквивалентное напряжение  Сравнивая величину эквивалентного напряжения с пределом прочности на растяжение, заключаем что прочность материала не обеспечена.

  ЗАДАНИЕ N 21  Тема: Расчет на прочность при кручении Стержень круглого поперечного сечения из пластичного материала работает на кручение. В расчетах по допускаемым напряжениям условие прочности имеет вид …

Решение: Для стержня круглого поперечного сечения из пластичного материала, работающего на кручение, условие прочности имеет вид   где   – предел текучести при чистом сдвиге,   – коэффициент запаса по текучести.

  ЗАДАНИЕ N 22  Тема: Расчет на жесткость при кручении 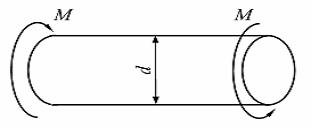Стержень скручивается двумя моментами (см. рисунок).        Из расчетов на прочность и жесткость максимально допустимая величина момента М равна ____ 

			0,0013
			0,0098
			0,0056
			0,0008

Решение: Запишем условие прочности для стержня   откуда  Составим условие жесткости  откуда  Таким образом, максимально допустимое значение 

 ЗАДАНИЕ N 23  Тема: Чистый сдвиг. Расчет на сдвиг (срез) 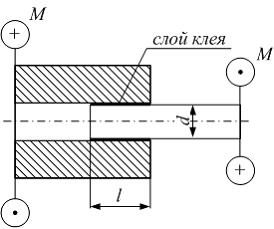На рисунке показано клеевое соединение втулки с валом, передающее крутящий момент. Задано: М, d, l,   – допускаемое касательное напряжение на срез клеевого слоя. Условие прочности на срез клеевого слоя имеет вид …

 ЗАДАНИЕ N 24  Тема: Крутящий момент. Деформации и напряжения 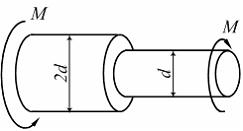В самых напряженных точках поперечного сечения вала касательные напряжения достигнут предела текучести тогда, когда значение момента М равно …

  ЗАДАНИЕ N 25  Тема: Основные понятия, определения, допущения и принципы Материал стержня (см. рисунок) – однонаправленный стеклопластик – является ____________ материалом.

			анизотропным
			изотропным
			абсолютно жестком
			абсолютно твердым

Решение: Свойства однонаправленного стеклопластика зависят от направления относительно волокон. Поэтому однонаправленный стеклопластик – материал анизотропный.

 ЗАДАНИЕ N 26  Тема: Модели прочностной надежности В сопротивлении материалов все тела считаются …

			абсолютно упругими
			абсолютно твердыми
			вязко-упругими
			упруго-вязко-пластичными

  ЗАДАНИЕ N 27  Тема: Внутренние силы и напряжения Интегральная связь между крутящим моментом   ( ) и касательными напряжениями имеет вид …

Решение: Площадь сечения можно разбить прямоугольной координатной сеткой на элементарные площадки.   и   – равнодействующие касательных напряжений, действующих на элементарной площадке,   − элементарные моменты относительно оси z. Крутящий момент   определяется как сумма элементарных моментов. Заменяя суммирование интегрированием по площади сечения, получаем 

 ЗАДАНИЕ N 28  Тема: Перемещение и деформация Вектор полного линейного перемещения точки в общем случае …

			можно разложить на три составляющих вектора, направленных вдоль координатных осей
			можно продолжить в направлении вектора
			нельзя разложить на три составляющих вектора, направленных вдоль координатных осей
			можно разложить только на два составляющих вектора, направленных вдоль координатных осей

  ЗАДАНИЕ N 29  Тема: Главные оси и главные моменты инерциим На рисунке показана плоская фигура. Известны величины:         u и v – главные оси. Главные моменты инерции равны ____   ____ 

			22,9; 2,5
			54; 32,5
			12,9; 12,5
			28,7; 5,8

Решение: Главные моменты инерции определим по формуле 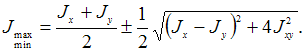 Подставляя числовые значения, получаем    Исходя из положения площади фигуры относительно осей u и v, можно сказать что   

 ЗАДАНИЕ N 30  Тема: Статические моменты. Центр тяжести плоской фигуры В системе координат xy координата центра тяжести трапеции по оси x равна ___ t.

			1,33
			1,67
			1,1
			1,4

  ЗАДАНИЕ N 31 Тема: Моменты инерции простых и сложных сечений 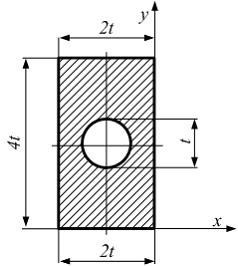Центробежный момент инерции относительно осей x, y равен ____ 

			–14,4
			–16
			16
			–18,5

Решение: Делим фигуру на прямоугольник (фигура I) и круг (фигура II). Используем формулу параллельного переноса. Учитываем, что центробежные моменты инерции прямоугольника и круга относительно собственных главных центральных осей равны нулю.

 ЗАДАНИЕ N 32  Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей Размерность осевого момента инерции …

			длина4
			длина3
			длина2
			длина5

(4)

 ЗАДАНИЕ N 1  Тема: Метод сил При раскрытии статической неопределимости системы методом сил система канонических уравнений имеет вид  Под обозначением   понимают …

			неизвестные силовые факторы
			перемещения от единичной силы
			перемещения от внешней нагрузки
			взаимные смещения точек системы

  ЗАДАНИЕ N 2  Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина Необходимо определить угол поворота поперечного сечения С (см. рисунок) с помощью интегралов Мора, который требуется вычислить способом Верещагина. Правильная эпюра изгибающего момента в единичном состоянии, построенная на сжатом слое, имеет вид …

			в
			г
			б
			а

Решение: Единичное состояние для определения угла поворота сечения С и эпюра изгибающего момента показаны на рисунке.

 ЗАДАНИЕ N 3  Тема: Статическая неопределимость. Степень статической неопределенности Система, четыре раза статически неопределимая (один раз внешним образом и три раза внутренним), показана на рисунке …

			2
			1
			3
			4

  ЗАДАНИЕ N 4  Тема: Расчет простейших статически неопределимых систем 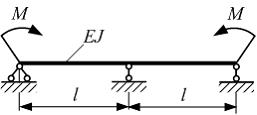На рисунке показана балка нагруженная моментами М. Эпюра изгибающих моментов имеет вид …

Решение: 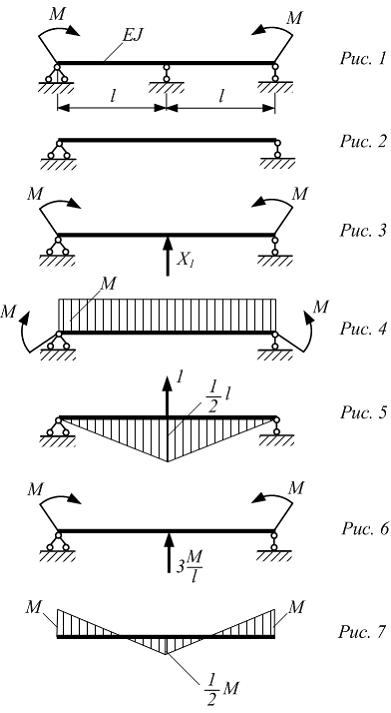Балка (рис. 1) один раз статически неопределима. Для раскрытия статической неопределимости используем метод сил. На рисунках 2 и 3 показана основная и эквивалентная системы. Каноническое уравнение метода сил имеет вид  Определяем коэффициенты канонического уравнение, используя для вычисления интегралов Мора способ Верещагина. Для этого строим эпюры изгибающих моментов в грузовом и единичном состояниях основной системы (рис. 4, 5) и перемножаем их. 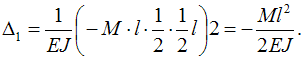Подставляя значения   и   в каноническое уравнение, получаем   Откуда   Подставляем значение   в эквивалентную систему (рис. 6) и строим окончательную эпюру изгибающего момента (рис. 7).

  ЗАДАНИЕ N 5  Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) 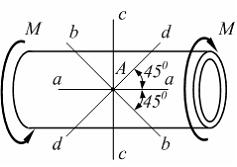На рисунке показана тонкостенная трубка, работающая на кручение. Главное напряжение   в точке А действует в направлении …

Решение: Выделим в окрестности точки А элемент стенки трубки двумя поперечными и двумя осевыми сечениями (рис. 1) и повернем его вокруг нормали   на угол, равный   (рис. 2). В этом случае касательные напряжения на гранях элемента будут равны нулю, а главные напряжения       Таким образом, главное напряжение   действует в направлении 

  ЗАДАНИЕ N 6 Тема: Виды напряженного состояния Стальной кубик вставлен без зазора в жесткую обойму (см. рис.). На верхнюю грань кубика действует равномерно распределенное давление интенсивности р. Поверхности кубика и обоймы абсолютно гладкие. Напряженное состояние кубика показано на рисунке …

			в
			г
			б
			а

Решение: 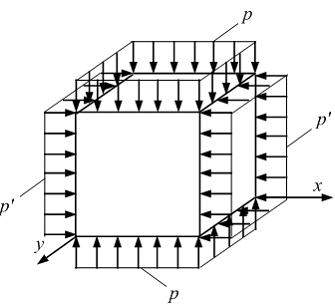Силы трения между абсолютно гладкими поверхностями кубика и обоймы отсутствуют. Поэтому касательные напряжения на гранях кубика равны нулю, и все грани являются главными площадками. В процессе сжатия ребра кубика, направленные вдоль осей x и y, стремятся удлиниться. Удлинение вдоль оси yпроисходит свободно. Удлинение вдоль оси x невозможно (мешает жесткая обойма). В связи с невозможностью удлинения вдоль оси x, со стороны вертикальных плоскостей обоймы на кубик действуют усилия в виде равномерно распределенных по площади нагрузок с некоторой интенсивностью  . Интенсивности р и   следует рассматривать как главные напряжения. Таким образом, из трех главных напряжений одно   (по фронтальной грани кубика). Поэтому напряженное состояние кубика плоское (рис. в).

 ЗАДАНИЕ N 7  Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Для изотропного материала главные оси деформированного состояния совпадают с …

			главными осями напряженного состояния
			главными центральными осями поперечного сечения
			осями симметрии кристаллической решетки
			ребрами элементарного объема

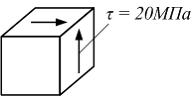
  ЗАДАНИЕ N 8  Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности На рисунке показано напряженное состояние в точке. Материал пластичный с пределом текучести   Коэффициент запаса по теории наибольших касательных напряжений равен …

			2,2
			6,7
			3,3
			1,5

Решение: Главные напряжения:      Эквивалентное напряжение по теории наибольших касательных напряжений  Коэффициент запаса 

 ЗАДАНИЕ N 9  Тема: Расчет на жесткость при кручении 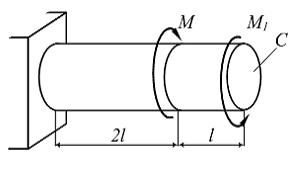На рисунке показан стержень, работающий на кручение. Известны величины: l,   М. Угол поворота сечения С равен нулю, когда момент   имеет значение …

			М

  ЗАДАНИЕ N 10  Тема: Расчет на прочность при кручении Стержень круглого поперечного сечения из хрупкого материала работает на кручение. Допускаемое напряжение определяется по формуле …

Решение: Напряженное состояние в точках стержня круглого поперечного сечения, работающего на кручение, – чистый сдвиг. Допускаемое напряжение определяется по формуле   где   – предел прочности при чистом сдвиге,   – коэффициент запаса по пределу прочности.

 ЗАДАНИЕ N 11  Тема: Чистый сдвиг. Расчет на сдвиг (срез) На рисунке показано клеевое соединение втулки с валом, передающее крутящий момент. Задано: М, d, l,   – допускаемое касательное напряжение на срез клеевого слоя. Условие прочности на срез клеевого слоя имеет вид …

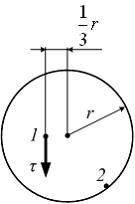 ЗАДАНИЕ N 12  Тема: Крутящий момент. Деформации и напряжения Пусть значение касательного напряжения   в точке 1 поперечного сечения равно   тогда  касательное напряжение в точке 2 равно ___ МПа.

			30
			25
			40
			35