Задание n 11

Тема: Расчеты стержней на прочность и жесткость Стержни фермы (см. рисунок) изготовлены из хрупкого материала. Условие прочности по допускаемым напряжениям в общем виде имеет вид …

 ЗАДАНИЕ N 12  Тема: Продольная сила. Напряжения и деформации 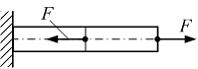На рисунке показан стержень, нагруженный силами F. Площадь поперечного сечения А, модуль упругости материала Е – известны. Продольная линейная деформация на левом грузовом участке стержня равна …

			0

  ЗАДАНИЕ N 13  Тема: Поперечная сила, изгибающий момент и их эпюры 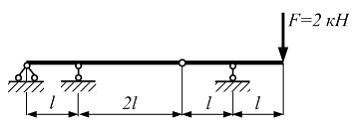Двухпролетная консольная балка с шарниром нагружена силой   Линейный размер  . Максимальное значение изгибающего момента в балке по абсолютной величине равно … (кНм)

			2
			0,5
			1
			2,5

Решение: Обозначим сечения над опорами и в шарнире буквами А, В, С, D. Отбросим связи, наложенные на балку, а их действие заменим реакциями. Используя уравнения статики, найдем реакции в опорах: На рисунке показаны положительные направления реакций. В сечениях А и С изгибающие моменты равны нулю. Сопоставим значения изгибающих моментов в сечениях B и D по абсолютной величине: Максимальное значение изгибающего момента в балке будет в сечении В и равно 2 кНм.

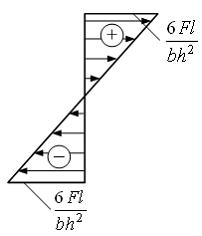
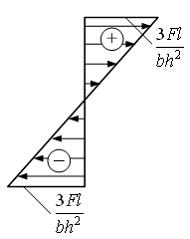
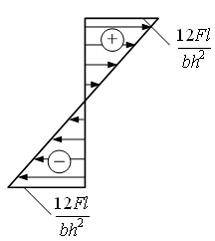
  ЗАДАНИЕ N 14  Тема: Напряжения в поперечном сечении стержня при плоском изгибе 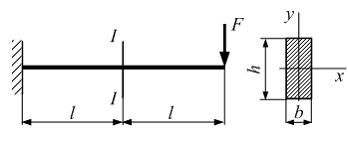Эпюра распределения нормальных напряжений по высоте сечения балки I–I с размерами b и h имеет вид …

Решение: Нормальные напряжения в поперечном сечении балки распределены по высоте по линейному закону    где   – значение изгибающего момента в сечении, в котором определяется нормальное напряжение;   – осевой момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости действия изгибающего момента в том же сечении; y – расстояние от главной центральной оси до точки, в которой определяется нормальное напряжение. В сечении I–I имеем 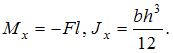 Верхняя половина сечения I–I работает на растяжение, нижняя – на сжатие. Максимальные значения нормальных напряжений по абсолютной величине возникают в точках при   и равны  По полученным значениям   построим эпюру распределения нормальных напряжений по высоте сечения I–I.

  ЗАДАНИЕ N 15  Тема: Перемещения при изгибе. Расчет балок на жесткость 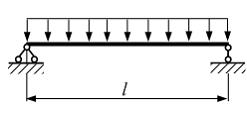Однопролетная балка длиной l, высотой h нагружена равномерно распределенной нагрузкой. Радиус кривизны нейтрального слоя балки в середине пролета равен  . Жесткость поперечного сечения на изгиб   по всей длине постоянна. Максимальное нормальное напряжение в балке равно … (Влияние поперечной силы на изменение кривизны не учитывать).

Решение: При изгибе балки кривизна нейтрального слоя связана с изгибающим моментом и жесткостью поперечного сечения на изгиб соотношением 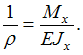 Следовательно, в середине пролета, в котором возникает максимальный изгибающий момент, имеем    Максимальное нормальное напряжение найдем по формуле  Учитывая, что  , получим 

 ЗАДАНИЕ N 16  Тема: Расчет балок на прочность 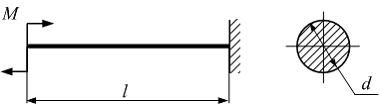Консольная балка длиной l нагружена моментом М. Значение допускаемого нормального напряжения   известно. Из расчета на прочность по нормальные напряжениям минимально допустимое значение диаметра поперечного сечения d равно …

 ЗАДАНИЕ N 17  Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина При вычислении интегралов Мора способом Верещагина …

			одна из подынтегральной функции должна быть линейной
			обе подынтегральные функции должны быть линейными
			обе подынтегральные функции должны быть нелинейными
			одна подынтегральная функция должна быть тригонометрической

 ЗАДАНИЕ N 18 отпр Тема: Статическая неопределимость. Степень статической неопределенности 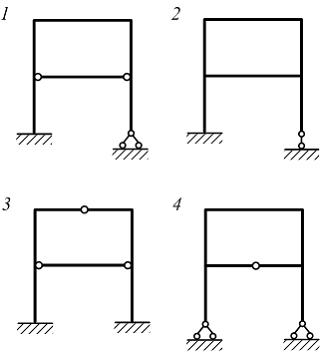Система, четыре раза статически неопределимая (один раз внешним образом и три раза внутренним), показана на рисунке …

			2
			1
			3
			4

 ЗАДАНИЕ N 19 о Тема: Расчет простейших статически неопределимых систем 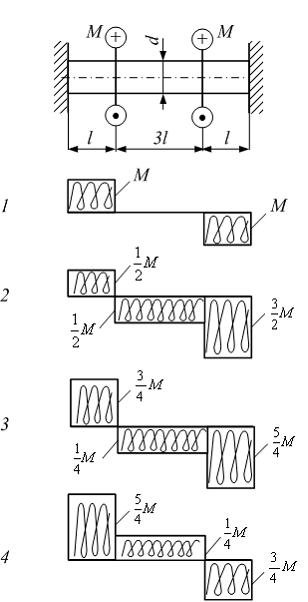Стержень нагружен моментами М. Модуль сдвига материала G, диаметр стержня d, размер l заданы. Эпюра крутящих моментов показана на рисунке …

			1
			3
			2
			4

 ЗАДАНИЕ N 20  Тема: Метод сил Для статически неопределимой системы один из вариантов правильно выбранной основной системы показан на рисунке …

			1
			2
			3
			4

 ЗАДАНИЕ N 21  Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности На рисунке показано напряженное состояние в точке. Материал пластичный с пределом текучести   Для перехода материала из упругого состояния в пластичное компоненты напряженного состояния следует увеличить в _____ раз(-а). Использовать теорию наибольших касательных напряжений.

			4,5
			9
			3
			5,3

 ЗАДАНИЕ N 22  Тема: Виды напряженного состояния 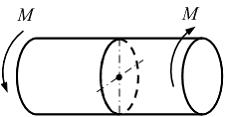На рисунке показан стержень, работающий на кручение. Напряженное состояние в центре тяжести поперечного сечения …

			нулевое
			объемное
			плоское
			линейное

  ЗАДАНИЕ N 23  Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Если         то линейные деформации: 

			0; 0; 0
			0; 0; 0,0015
			0,0025; 0,0025; 0,0025
			0,062; 0; 0

Решение: Согласно обобщенному закону Гука, линейные деформации элементарного объема зависят только от нормальных напряжений, действующих на его гранях. Поэтому в нашем случае 

 ЗАДАНИЕ N 24  Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) На рисунке показан элементарный параллелепипед и напряжения на его гранях:     Главные напряжения   соответственно равны: ____ МПа, ____ МПа, ____МПа.

			5, -5, -10
			-10, -5, 5
			5, 5, -10
			5, -10, -20

  ЗАДАНИЕ N 25  Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Поперечное сечение сжатого стержня – равнобедренный треугольник шириной основания b и высотой b. При уменьшении высоты треугольника в два раза, при прочих равных условиях, значение критической силы …  При решении учитывать, что стержни, в обоих вариантах, имеют большую гибкость.

			уменьшится в 6 раз
			не изменится
			уменьшится в 2 раза
			увеличится в 2 раза

Решение: Воспользуемся формулой Эйлера. В первом варианте, минимальный момент инерции сечения 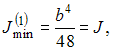а во втором 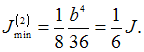Следовательно, во втором варианте значение критической силы уменьшится в шесть раз.

 ЗАДАНИЕ N 26  Тема: Влияние условий закрепления концов стержня на величину критической силы При замене шарниров (рис. а) в сжатом стержне на жесткие защемления (рис. б) значение гибкости …

			уменьшится в 2 раза
			не изменится
			увеличится в 2 раза
			уменьшится в 4 раза

 ЗАДАНИЕ N 27  Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня При потере устойчивости сжатого стержня изгиб стержня происходит в плоскости …

			наименьшей жесткости
			наибольшей жесткости
			равнонаклоненной к осям симметрии
			расположенной в любом направлении

  ЗАДАНИЕ N 28  Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость Поперечное сечение стержня состоит из четырех равнобоких уголков. Наиболее рациональная форма, с позиции устойчивости, показана на схеме …

			в
			а
			г
			б

Решение: Площади поперечного сечения для всех вариантов форм одинаковы. При проектировании формы поперечного сечения стержня, с позиции устойчивости, необходимо при одинаковой площади стремиться к получению наибольших центральных моментов инерции. Вместе с тем надо стремиться к тому, чтобы все центральные моменты инерции сечения были равны. Таким критериям отвечает форма на схеме «в».

 ЗАДАНИЕ N 29  Тема: Крутящий момент. Деформации и напряжения При кручении стержня круглого поперечного сечения угол сдвига изменяется вдоль радиуса по …

			линейному закону
			по закону синуса
			по закону квадратной параболы
			по закону косинуса

  ЗАДАНИЕ N 30  Тема: Расчет на прочность при кручении 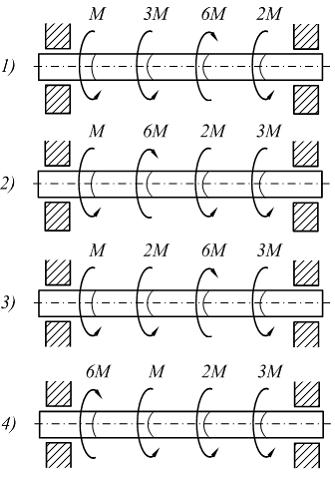На рисунках показаны четыре варианта нагружения одного и того же вала моментами М, 2М, 3М и 6М. Вал будет иметь наименьший диаметр при его нагружении по варианту …

			3
			4
			1
			2

Решение: Эпюры крутящих моментов для четырех вариантов нагружения вала имеют вид (смотри рис. 1). Наименьшее значение максимального крутящего момента, а значит и наименьший диаметр, вал будет иметь в третьем варианте нагружения.

  ЗАДАНИЕ N 31  Тема: Чистый сдвиг. Расчет на сдвиг (срез) 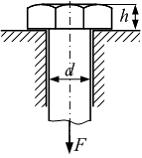На рисунке показан болт, нагруженный силой F. Дано:       – допускаемое касательное напряжение на срез головки болта. Минимально допустимая высота головки болта из расчета на срез равна ___ см.

			0,8
			1,6
			2,5
			1,25

Решение: Срез головки болта происходит по цилиндрической поверхности диаметром d и высотой h (см. рисунок). Полагаем, что напряжения по высоте h не изменяются. Запишем уравнение равновесия   откуда   Условие прочности на срез имеет вид   откуда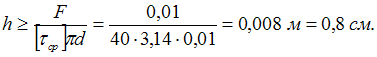 

 ЗАДАНИЕ N 32  Тема: Расчет на жесткость при кручении На рисунке показан опасный участок вала, работающий на кручение при значениях:      По результатам проверочных расчетов на жесткость и прочность можно сказать, что …

			жесткость и прочность вала не обеспечены
			прочность обеспечена, а жесткость не обеспечена
			прочность и жесткость вала обеспечены
			жесткость обеспечена, а прочность не обеспечена

(3)

 ЗАДАНИЕ N 1  Тема: Расчет простейших статически неопределимых систем На рисунке показан стержень нагруженный силами F и моментами М. Размер l, диаметр d, модули упругости Е и G заданы. Крутящий момент и продольная сила в сечении С-С, соответственно, равны …

			0, 0

 ЗАДАНИЕ N 2  Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина Для определения перемещений в кривых плоских стержнях с помощью интегралов Мора, без учета влияния поперечных и продольных сил, используется формула 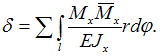  Величина   является …

			длиной элемента   оси стержня
			кривизной оси стержня
			радиусом кривизны оси стержня
			средней кривизной оси стержня

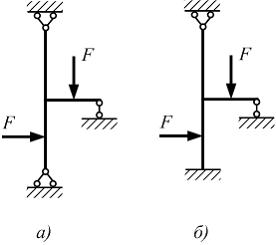
 ЗАДАНИЕ N 3  Тема: Статическая неопределимость. Степень статической неопределенности          Статически определимая система показана на рисунке …

			в
			а
			г
			б

 ЗАДАНИЕ N 4  Тема: Метод сил Система канонических уравнений метода сил имеет вид   Левая часть каждого уравнения это перемещение в направлении i-ой отброшенной связи, вызванное …

			реакциями отброшенных связей и внешней нагрузкой
			внешней нагрузкой
			реакциями отброшенных связей
			силой

  ЗАДАНИЕ N 5  Тема: Напряжения в поперечном сечении стержня при плоском изгибе 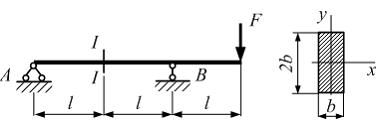Однопролетная консольная балка прямоугольного сечения с размерами b и 2b нагружена силой F. Линейные размеры b и l = 20b заданы. В сечении I–I значение максимального касательного напряжения равно τ. Максимальное нормальное напряжение в балке равно …

Решение: Используя уравнения статики, определим реакции  опор А и В:  Касательное напряжение в любой точке поперечного сечения балки определяется по формуле Д. И. Журавского Для прямоугольного сечения максимальное касательное напряжение возникает в точках на нейтральной линии и равно   где Q – значение поперечной силы в данном сечении; А – площадь поперечного сечения. В сечении I–I имеем    Тогда 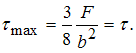 Максимальное нормальное напряжение возникает в сечении балки над опорой В, где действует максимальный изгибающий момент   Значение максимального нормального напряжения вычислим по формуле   где   – момент сопротивления. Для прямоугольного сечения 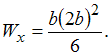 После вычислений, учитывая, что   и   получим 

  ЗАДАНИЕ N 6  Тема: Расчет балок на прочность 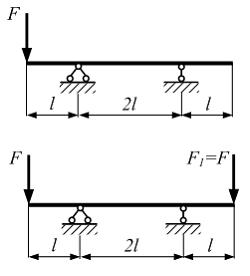Однопролетная двухконсольная балка нагружена силой F. К балке дополнительно прикладывается сила   С изменением схемы нагружения прочность балки …

			не изменится
			уменьшится в два раза
			увеличится в два раза
			уменьшитсяв в четыре раза

Решение: Размеры балки и материал не изменились. Поэтому при оценке прочности необходимо учитывать только значения внутренних силовых факторов: поперечной силы и изгибающего момента. В обоих вариантах нагружения максимальные значения внутренних силовых факторов одинаковы. Следовательно, прочность балки не изменится.