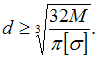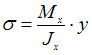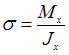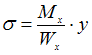Решение:

 ЗАДАНИЕ N 20  Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей Момент инерции площади – величина …

			положительная
			положительная или равна нулю
			положительная или отрицательная
			отрицательная или равна нулю

  ЗАДАНИЕ N 21  Тема: Влияние условий закрепления концов стержня на величину критической силы 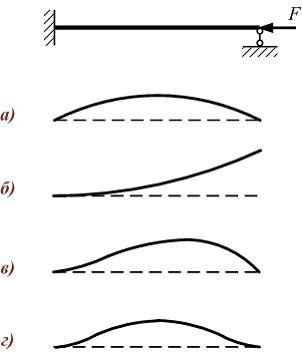Стержень, схема закрепления которого показана на верхнем рисунке, сжимается силой F. Форма потери устойчивости стержня представлена на схеме …

			в
			а
			г
			б

Решение: При заданной схеме закрепления стержня прогиб и угол поворота крайнего левого сечения стержня равны нулю. Вертикальное перемещение крайнего правого сечения равно нулю, но разрешается поворот сечения. Этим условиям соответствует форма потери устойчивости, показанная на схеме «в».

 ЗАДАНИЕ N 22  Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Критическим называется напряжение, возникающее в поперечном сечении сжатого стержня при значении нагрузки, вызывающей …

			потерю устойчивости стержня
			появление пластических деформаций
			рост деформаций, превышающих допустимые
			возникновение продольных колебаний в стержне

  ЗАДАНИЕ N 23 Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость Коэффициенты a и b в формуле Тетмайера-Ясинского имеют размерность …

			напряжения
			силы
			длины
			площади

Решение: Гибкость стержня   величина безразмерная. Поэтому, чтобы размерность левой и правой частей формулы была одинакова, коэффициенты a и bдолжны иметь размерность напряжения.

  ЗАДАНИЕ N 24  Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Возможность применения формулы Эйлера для определения критической силы сжатого стержня, изготовленного из заданного материала, устанавливается по величине …

			гибкости
			площади сечения
			длины
			радиуса инерции сечения

Решение: Формула Эйлера для определения критической силы сжатого стержня справедлива, если напряжения в стержне не превышают предела пропорциональности, то есть 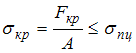  или   где   − гибкость стержня. Если из неравенства выразить гибкость, то условие применения формулы Эйлера получит вид 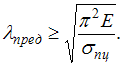 Следовательно, величина гибкости устанавливает возможность применения формулы Эйлера.

  ЗАДАНИЕ N 25  Тема: Расчет на жесткость при кручении На рисунке показан опасный участок вала, работающий на кручение при значениях:      По результатам проверочных расчетов на жесткость и прочность можно сказать, что …

			жесткость и прочность вала не обеспечены
			прочность обеспечена, а жесткость не обеспечена
			прочность и жесткость вала обеспечены
			жесткость обеспечена, а прочность не обеспечена

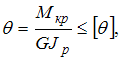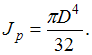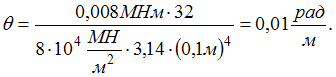
Решение: Условие жесткости имеет вид  где  Определяем относительный угол закручивания на данном участке вала. Условие прочности имеет вид   где  Определяем максимальное касательное напряжение 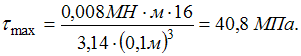Сравнивая   с   и   с  , делаем заключение, что жесткость и прочность вала не обеспечены. В этом случае параметры системы   следует изменить таким образом, чтобы условия жесткости и прочности выполнялись.

  ЗАДАНИЕ N 26  Тема: Расчет на прочность при кручении Стержень круглого поперечного сечения из пластичного материала работает на кручение. При расчете по допускаемым касательным напряжениям за предельное напряжение принимается …

			предел текучести при чистом сдвиге
			предел текучести при растяжении
			предел прочности при чистом сдвиге
			предел упругости при чистом сдвиге

Решение: Предел текучести при чистом сдвиге считается предельным напряжением в расчетах по допускаемым напряжениям стержней из пластичного материала, работающих на кручение.

  ЗАДАНИЕ N 27  Тема: Крутящий момент. Деформации и напряжения Пусть значение касательного напряжения   в точке 1 поперечного сечения равно   тогда  касательное напряжение в точке 2 равно ___ МПа.

			30
			25
			40
			35

Решение: При кручении стержня касательные напряжения в точках круглого поперечного сечения определяются по формуле 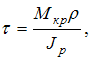  где ρ – расстояние от центра тяжести поперечного сечения до точки, в которой определяется касательное напряжение. Зависимость τ от ρ линейная. Поэтому значение касательного напряжения в точке 2 в три раза больше напряжения в точке 1.

 ЗАДАНИЕ N 28  Тема: Чистый сдвиг. Расчет на сдвиг (срез) Напряженное состояние «чистый сдвиг» показано на  рисунке. Штриховыми линиями показан характер деформации. Углом сдвига называется угол …

  ЗАДАНИЕ N 29  Тема: Перемещения при изгибе. Расчет балок на жесткость 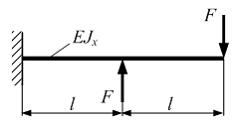Консольная балка длиной   нагружена силами F. Модуль упругости материала Е, осевой момент инерции сечения   заданы. Прогиб концевого сечения примет значение  , когда значение силы F равно …

Решение: Воспользуемся универсальным уравнением упругой линии балк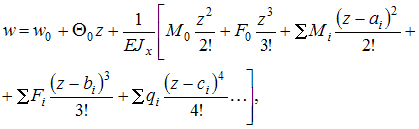и  где   и   – начальные параметры (прогиб и угол поворота в начале координат);  ,   – значения момента и силы в начале координат. Составим расчетную схему. Начало координат расположим в крайнем левом сечении балки. 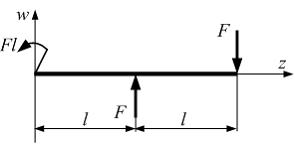Из условий равновесия балки найдем  Начало координат совпадает с заделкой. В начале координат прогиб   и угол поворота  =0. Уравнение упругой линии имеет вид 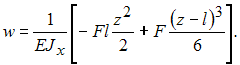 Полагая, что  , определим прогиб свободного конца балки 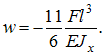 Знак «минус» показывает, что перемещение направлено вниз. Из условия   получим 

 ЗАДАНИЕ N 30  Тема: Напряжения в поперечном сечении стержня при плоском изгибе Для определения нормальных напряжений в точках поперечного сечения балки при плоском изгибе используется формула …

  ЗАДАНИЕ N 31  Тема: Поперечная сила, изгибающий момент и их эпюры 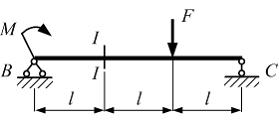Однопролетная балка ВС длиной   нагружена силой F и моментом М. Поперечная сила в сечении I–I будет равна нулю, если значение М равно …

Решение: Отбросим связи, наложенные на балку, и их действие заменим реакциями  Рассекаем балку произвольным сечением на левом участке на две части. Отбросим правую часть. Длина левой части изменяется в пределах    Действие отброшенной части на оставшуюся заменяем внутренними силовыми факторами: поперечной силой   и изгибающим моментом 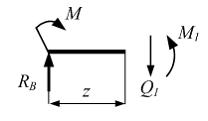 Из уравнения равновесия следует  Сечение I–I   принадлежит левому участку. Поэтому поперечная сила в сечении I–I будет равна нулю, когда   Учитывая это условие , составим сумму моментов всех сил, действующих на балку, относительно точки С  отсюда 

  ЗАДАНИЕ N 32  Тема: Расчет балок на прочность Консольная балка длиной l нагружена моментом М. Значение допускаемого нормального напряжения   известно. Из расчета на прочность по нормальные напряжениям минимально допустимое значение диаметра поперечного сечения d равно …

Решение: Форма и размеры поперечного сечения по длине балки не меняются. Поэтому   где  Для круглого сечения 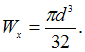 Из условия прочности по нормальным напряжениям

253