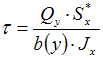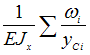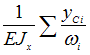Решение:

  ЗАДАНИЕ N 6  Тема: Главные оси и главные моменты инерциим Плоская фигура имеет бесконечное множество главных центральных осей инерции, если число осей симметрии фигуры …

			больше двух
			меньше трех
			равно единице
			равно двум

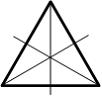
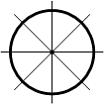
Решение:   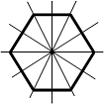  Если число осей симметрии фигуры больше двух, то любая ось, проходящая через ее центр тяжести, является главной центральной осью и моменты инерции относительно этих осей равны. Примером могут служить фигуры в форме равностороннего треугольника, правильного шестиугольника, круга (см. рисунок).

  ЗАДАНИЕ N 7  Тема: Моменты инерции простых и сложных сечений Момент инерции правильного шестиугольника с размером стороны а относительно оси x равен …

Решение: Разделим шестиугольник на прямоугольник со сторонами а и   и четыре треугольника ( смотри рисунок). Тогда   где   – основание и высота прямоугольника,   – основание и высота треугольника. Подставляя значения   в формулу, получаем 

 ЗАДАНИЕ N 8  Тема: Статические моменты. Центр тяжести плоской фигуры Сечение состоит из двутавра и швеллера. В системе координат   координаты центра тяжести фигуры 

  ЗАДАНИЕ N 9  Тема: Испытание конструкционных материалов на растяжение и сжатие      Вид образца после испытания показан на рисунке. Испытание проводилось по варианту …

			а
			г
			б
			в

Решение: Видно, что до испытания образец имел кубическую форму. Значит, он предназначен для испытаний на сжатие. Картина разрушения (две усеченные пирамиды) – типичная картина разрушения образца из цементно-песчаной смеси при больших силах трения между поверхностями образца и поверхностями плит испытательной машины.

  ЗАДАНИЕ N 10  Тема: Расчеты стержней на прочность и жесткость 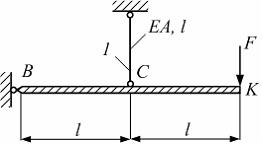Система, показанная на рисунке, нагружена силой F. Известны величины:   – перемещение шарнира С. Вес абсолютно жесткого элемента ВКв расчетах не учитывать. Значение силы F равно …

Решение: Рассмотрим равновесие элемента ВК (см. рисунок). Уравнение равновесия имеет вид   откуда   Удлинение стержня 1 равно перемещению точки С.  Следовательно, 

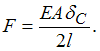
  ЗАДАНИЕ N 11  Тема: Механические свойства и механические характеристики материалов Коэффициент Пуассона  для изотропного материала изменяется в пределах …

Решение: Область изменения коэффициента Пуассона изотропного материала 

 ЗАДАНИЕ N 12  Тема: Продольная сила. Напряжения и деформации Колонна высотой H (см. рисунок) находится под действием собственного веса и силы F. Удельный вес материала колонны   (вес единицы объема), площадь поперечного сечения А – известны. Максимальные нормальные напряжения в поперечном сечении колонны равны …

  ЗАДАНИЕ N 13  Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности Классические теории прочности: 1) теория наибольших нормальных напряжений, 2) теория наибольших линейных деформаций удлинения, 3) теория наибольших касательных напряжений, 4) теория удельной потенциальной энергии формоизменения. Для оценки прочности хрупких материалов используются ________ теории прочности.

			1 и 2
			3 и 4
			1 и 4
			2 и 3

Решение: Для оценки прочности хрупких материалов используются первая и вторая  теории прочности.

 ЗАДАНИЕ N 14  Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями 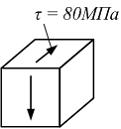На рисунке показано напряженное состояние в точке. Модуль упругости   коэффициент Пуассона  . Относительное изменение объема равно …

			0

 ЗАДАНИЕ N 15  Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) На рисунке показан стержень, растянутый силами F, и элементарный объем выделенный гранями, параллельными плоскостям стержня. При повороте элементарного объема вокруг оси «u» на угол, равный 45⁰, напряженное состояние …

			не изменится
			становится плоским
			становится объемным
			становится плоским (чистый сдвиг)

  ЗАДАНИЕ N 16  Тема: Виды напряженного состояния Тип напряженного состояния в точке тела, нагруженного произвольной системой сил, устанавливается по …

			количеству главных напряжений не равных нулю
			значениям главных напряжений не равных нулю
			известным механическим характеристикам материала
			характеру внешней нагрузки

Решение: Тип напряженного состояния в точке тела, нагруженного произвольной системой сил, устанавливается по числу главных напряжений не равных нулю.  Одно из главных напряжений не равно нулю – напряженное состояние линейное. Два главных напряжения не равны нулю – напряженное состояние плоское. Все три главных напряжения не равны нулю – напряженное состояние объемное.

  ЗАДАНИЕ N 17  Тема: Напряжения в поперечном сечении стержня при плоском изгибе Для определения касательных напряжений в точках поперечного сечения балки, при плоском поперечном изгибе, используют формулу …

Решение: 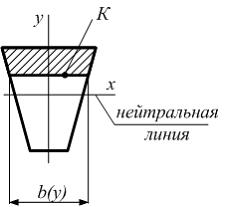Касательные напряжения в точках поперечного сечения балки при плоском поперечном изгибе определяют по формуле Журавского 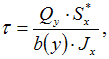где   – значение поперечной силы в данном сечении;   – статический момент относительно нейтральной линии  площади сечения расположенной выше (или ниже) точки К в которой определяется касательное напряжение линии (см. рисунок, заштрихованная площадь);   – ширина поперечного сечения;   – осевой момент инерции сечения относительно главной центральной оси (нейтральной линии).

 ЗАДАНИЕ N 18  Тема: Поперечная сила, изгибающий момент и их эпюры 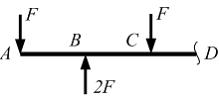На рисунке показана отсеченная часть балки и нагрузка, действующая на нее. Неверным является утверждение, что поперечная сила …

			на участке ВС меняется по линейному закону
			на участке CD равна нулю
			на участке АВ постоянна
			в сечении В изменяется скачком

 ЗАДАНИЕ N 19  Тема: Перемещения при изгибе. Расчет балок на жесткость Консольная балка длиной   нагружена моментом   Поперечное сечение балки прямоугольник:     Модуль упругости материала   Радиус кривизны балки в сечении I–I равен ___ (м).

			3,6
			6
			5,2
			4,8

  ЗАДАНИЕ N 20  Тема: Расчет балок на прочность Консольная балка длиной   нагружена равномерно распределенной нагрузкой интенсивности   Поперечное сечение – равнобедренный треугольник. Допускаемое нормальное напряжение для материала балки   Из расчета на прочность по нормальным напряжениям размер поперечного сечения балки b равен ____ (см).

			3
			5
			4
			6

Решение: Максимальные нормальные напряжения в балке определяются по формуле  В случае, когда размеры поперечного сечения балки по длине не меняются, максимальные нормальные напряжения возникают в сечении балки, где действует максимальный изгибающий момент и в точках, наиболее удаленных от нейтральной линии. Нейтральная линия совпадает с главной центральной осью поперечного сечения перпендикулярной плоскости действия изгибающего момента. Максимальный изгибающий момент   действует в сечении балки вблизи заделки. Центр тяжести треугольного сечения расположен на расстоянии   от основания треугольника, то есть   Осевой момент инерции относительно главной центральной оси x равен   а расстояние  После вычислений  Из условия прочности по нормальным напряжениям  получим 

  ЗАДАНИЕ N 21  Тема: Модели прочностной надежности 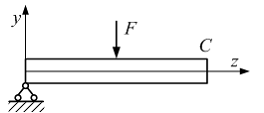Правый конец балки (см. рисунок) должен быть закреплен так, чтобы сечение С не перемещалось вдоль координатных осей z и y и не поворачивалось в плоскости zy. Опора, отвечающая таким требованиям, называется …

			жестким защемлением
			шарнирно подвижной
			шарнирно неподвижной
			скользящим защемлением

Решение: Опора, отвечающая требованиям задания, называется жестким защемлением. Условное обозначение такой опоры показано на рисунке.

  ЗАДАНИЕ N 22  Тема: Основные понятия, определения, допущения и принципы Тело не разрушается под воздействием внешних сил, если его материал обладает свойством …

			прочности
			упругости
			жесткости
			пластичности

Решение: Все материалы обладают способностью сопротивляться разрушению под воздействием внешних сил. Это свойство материалов называется прочностью.

 ЗАДАНИЕ N 23  Тема: Внутренние силы и напряжения Размерность напряжения …

  ЗАДАНИЕ N 24  Тема: Перемещение и деформация Точка К деформируемого тела перемещается в пространстве. Известны полное перемещение   и перемещения вдоль координатных осей x, y (u и v). Величина перемещения вдоль оси z (w) определяется по формуле …

Решение: Полное перемещение точки равно длине диагонали прямоугольного параллелепипеда, ребрами которого являются перемещения вдоль координатных осей. Полное перемещение и перемещения по осям связаны зависимостью   откуда 

  ЗАДАНИЕ N 25  Тема: Статическая неопределимость. Степень статической неопределенности Степень статической неопределимости плоской рамы равна …

			четырем
			трем
			пяти
			двум

Решение: На раму наложено семь внешних связей (две угловые и пять линейных). Для обеспечения кинематической неизменяемости рамы необходимы только три связи. Значит число дополнительных связей равно четырем. Следовательно, рама четыре раза статически неопределима.

  ЗАДАНИЕ N 26  Тема: Метод сил Результат умножения симметричной эпюры на кососимметричную – …

			ноль
			положительное число
			отрицательное число
			число положительное и отрицательно

Решение: На рисунке показаны симметричная и кососимметричная эпюры. Буквами   и   обозначены центры тяжестей площадей   и   Перемножим площади   на ординаты   и сложим произведения. Получим нулевой результат.

 ЗАДАНИЕ N 27  Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина При плоском изгибе, без учета поперечных сил, интеграл Мора вычисляется способом Верещагина по формуле 

 ЗАДАНИЕ N 28  Тема: Расчет простейших статически неопределимых систем На рисунке показан стержень нагруженный силами F и моментами М. Размер l, диаметр d, модули упругости Е и G заданы. Крутящий момент и продольная сила в сечении С-С, соответственно, равны …

			0, 0

  ЗАДАНИЕ N 29  Тема: Чистый сдвиг. Расчет на сдвиг (срез) На рисунке показано клеевое соединение трех листов. Известно:       – допускаемое касательное напряжение на срез клеевого слоя. Максимально допустимое значение силы F из расчета на срез клеевого слоя равно ___ кН.

			14,4
			7,2
			3,6
			5,2

Решение: 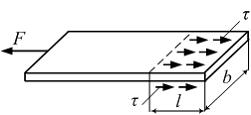Рассмотрим равновесие среднего листа (см. рисунок). Полагаем, что касательные напряжения распределены по площади среза равномерно. Условие равновесия и условие прочности на срез имеют вид:     откуда Подставляя числовые значения, получаем 

  ЗАДАНИЕ N 30  Тема: Расчет на прочность при кручении На рисунках показаны четыре варианта нагружения одного и того же вала моментами М, 2М, 3М и 6М. Вал будет иметь наименьший диаметр при его нагружении по варианту …

			3
			4
			1
			2

Решение: Эпюры крутящих моментов для четырех вариантов нагружения вала имеют вид (смотри рис. 1). Наименьшее значение максимального крутящего момента, а значит и наименьший диаметр, вал будет иметь в третьем варианте нагружения.

  ЗАДАНИЕ N 31  Тема: Крутящий момент. Деформации и напряжения На рисунке показан стержень, работающий на кручение. Максимальное растягивающее напряжение в точке К действует в направлении …

			4−4
			3−3
			1−1
			2−2

Решение: Если в окрестности точки К двумя поперечными, двумя продольно-осевыми и цилиндрическим сечениями выделить элементарный объем, то на его гранях будут действовать касательные напряжения. Напряженное состояние показано на рисунке 1 через плоский элемент. При повороте на угол   касательные напряжения на его гранях исчезают, но появляются нормальные напряжения, показанные на рисунке 2.

 ЗАДАНИЕ N 32  Тема: Расчет на жесткость при кручении На рисунке показан стержень, испытывающий деформацию кручение. Известные величины: M, d, G – модуль сдвига материала стержня,   – допустимый относительный угол закручивания. Условие жесткости для стержня имеет вид …

(12)

 ЗАДАНИЕ N 1  Тема: Механические свойства и механические характеристики материалов Материал, механические характеристики которого не зависят от направления, называется …

			изотропным
			однородным
			сплошным
			анизотропным

  ЗАДАНИЕ N 2  Тема: Продольная сила. Напряжения и деформации Отношение значений продольных сил в сечениях С-С и К-К (см. рисунок) равно …

			1
			–1

Решение: Оба сечения принадлежат одному грузовому участку. Величина продольной силы не зависит от площади поперечного сечения. Поэтому отношение 

  ЗАДАНИЕ N 3  Тема: Расчеты стержней на прочность и жесткость Известны величины:   (см. рисунок). Зазор   полностью перекрывается, когда сила F становится равной …

Решение: Когда зазор полностью перекрывается, перемещение сечения С стержня становится равным величине зазора.   откуда 

 ЗАДАНИЕ N 4  Тема: Испытание конструкционных материалов на растяжение и сжатие  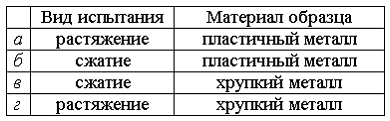   Вид образца после испытаний показан на рисунке. Испытание проводилось по варианту …

			б
			а
			г
			в

  ЗАДАНИЕ N 5  Тема: Расчет балок на прочность Консольная балка прямоугольного сечения нагружена силой   Допускаемое нормальное напряжение для материала балки  , линейный размер  . Наибольшая длина консоли   из расчета на прочность по нормальным напряжениям равна ___ см.

			64
			32
			128
			96

Решение: Условие прочности по допускаемым нормальным напряжениям имеет вид . Наибольшее нормальное напряжение действует в сечении балки вблизи заделки, где возникает максимальный изгибающий момент  , и определяется по формуле  Осевой момент сопротивления при заданных размерах поперечного сечения равен  Следовательно,  Откуда   или 

  ЗАДАНИЕ N 6  Тема: Поперечная сила, изгибающий момент и их эпюры 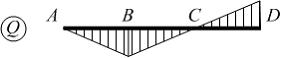На рисунке показана эпюра поперечных сил. Неверным является утверждение, что …

			на эпюре изгибающих моментов в сечении В излом
			в сечении С изгибающий момент имеет экстремальное значение
			распределенная нагрузка на участках AB и BD имеет противоположное направление
			на участке балки AD действует равномерно распределенная нагрузка

Решение: В сечении, в котором к балке приложена сосредоточенная сила: а) на эпюре поперечных сил будет скачок на величину и в направлении этой силы; б) на эпюре изгибающих моментов излом. Поэтому неверным является утверждение, что на эпюре изгибающих моментов в сечении В излом.

  ЗАДАНИЕ N 7  Тема: Напряжения в поперечном сечении стержня при плоском изгибе 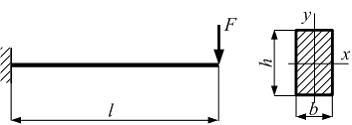Консоль длиной l прямоугольного сечения с размерами b и h нагружена силой F. При увеличении линейных размеров балки в два раза максимальное нормальное напряжение …

			уменьшится в 4 раза
			уменьшится в 2 раза
			не изменится
			увеличится в 4 раза

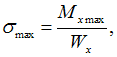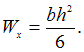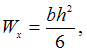
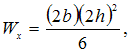
Решение: Форма и размеры поперечного сечения по длине консоли не изменяются. Поэтому, для определения максимального нормального напряжения воспользуемся формулой  где  Для первого варианта:     Для второго      Следовательно, при увеличении линейных размеров в два раза максимальное нормальное напряжение уменьшится в четыре раза.

  ЗАДАНИЕ N 8  Тема: Перемещения при изгибе. Расчет балок на жесткость 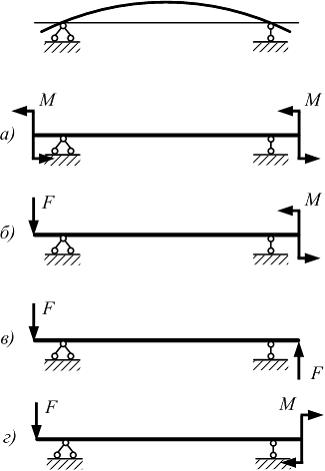На рисунке показан примерный вид изогнутой оси балки. Схема нагружения балки, соответствующая представленной форме изгиба, показана на схеме …

			г
			а
			в
			б

Решение: Вид изогнутой оси балки показывает, что верхние слои на всех силовых участках работают на деформацию растяжения. Это соответствует нагружению балки показанному на схеме «г».

  ЗАДАНИЕ N 9  Тема: Крутящий момент. Деформации и напряжения На рисунке показан стержень, работающий на кручение. Максимальное растягивающее напряжение в точке К действует в направлении …

			4−4
			3−3
			1−1
			2−2

Решение: Если в окрестности точки К двумя поперечными, двумя продольно-осевыми и цилиндрическим сечениями выделить элементарный объем, то на его гранях будут действовать касательные напряжения. Напряженное состояние показано на рисунке 1 через плоский элемент. При повороте на угол   касательные напряжения на его гранях исчезают, но появляются нормальные напряжения, показанные на рисунке 2.

  ЗАДАНИЕ N 10  Тема: Чистый сдвиг. Расчет на сдвиг (срез) На рисунке показано клеевое соединение трех листов. Известно:       – допускаемое касательное напряжение на срез клеевого слоя. Максимально допустимое значение силы F из расчета на срез клеевого слоя равно ___ кН.

			14,4
			7,2
			3,6
			5,2

Решение: Рассмотрим равновесие среднего листа (см. рисунок). Полагаем, что касательные напряжения распределены по площади среза равномерно. Условие равновесия и условие прочности на срез имеют вид:     откуда Подставляя числовые значения, получаем 

  ЗАДАНИЕ N 11  Тема: Расчет на прочность при кручении Стержень с круглым поперечным сечением, изготовленный из пластичного материала, работает на кручение. Опасным (предельным) напряжением для стержня является …

			предел текучести при чистом сдвиге
			предел прочности при чистом сдвиге
			предел упругости при чистом сдвиге
			предел текучести при растяжении

Решение: Напряженное состояние материала стержня – чистый сдвиг. На рисунке показана диаграмма напряжений при чистом сдвиге для пластичного материала с ярко выраженной площадкой текучести. За опасное состояние пластичного материала принимается процесс текучести, когда угол сдвига растет при постоянном касательном напряжении, которое называется пределом текучести материала при чистом сдвиге   Если диаграмма напряжений не имеет площадки текучести, то принято говорить об условном пределе текучести при чистом сдвиге. При определении условного предела текучести вводится допуск на остаточную деформацию после снятия нагрузки аналогично допуску на остаточную деформацию при определении условного предела текучести при растяжении-сжатии (см. учебник В. И. Феодосьева «Сопротивление материалов», § 16. Основные механические характеристики материалов).

  ЗАДАНИЕ N 12  Тема: Расчет на жесткость при кручении 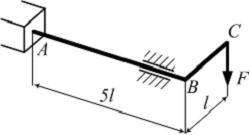Левый конец стержня АВ (см. рисунок) жестко защемлен, правый установлен в подшипнике скольжения. Элемент ВС абсолютно жесткий. Известны величины: l,   – жесткость поперечного сечения стержня АВ на кручение,   – допускаемая величина вертикального перемещения точки С. Максимально допустимое значение силы F равно …

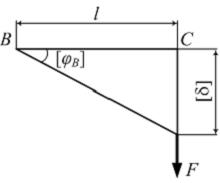Решение: Стержень АВ скручивается моментом Fl. Допускаемый угол поворота поперечного сечения В стержня АВ равен   (см. рисунок). С другой стороны 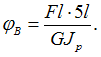  Условие жесткости имеет вид 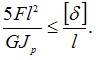  Откуда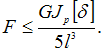 

 ЗАДАНИЕ N 13  Тема: Модели прочностной надежности Колонна здания относится к классу …

			стержней
			оболочек
			массивов
			пластин

  ЗАДАНИЕ N 14  Тема: Основные понятия, определения, допущения и принципы Для того чтобы перемещения отдельных точек конструкции не превышали определенных наперед заданных величин, конструкция должна обладать свойством …

			жесткости
			упругости
			прочности
			пластичности

Решение: Под жесткостью понимают способность конструкции сопротивляться внешним нагрузкам без существенного изменения геометрических размеров. Поэтому правильный ответ «конструкция должна обладать свойством жесткости».

  ЗАДАНИЕ N 15  Тема: Внутренние силы и напряжения Значения полного и касательного напряжений в точке сечения соответственно равны 5 МПа и  3 МПа. Значение нормального напряжения в этой же точке сечения равно _____ МПа.

			4
			2
			8
			1,41

Решение: Полное, нормальное и касательное напряжения в точке сечения связаны зависимостью   откуда   Подставляя числовые значения, получаем 

 ЗАДАНИЕ N 16  Тема: Перемещение и деформация 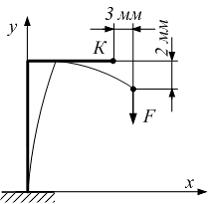В процессе нагружения рамы силой F точка К перемещается вдоль оси x на 3 мм, а вдоль оси y на 2 мм (см. рисунок). Полное перемещение точки Кравно _____ мм.

			3,6
			5
			2,24
			1

  ЗАДАНИЕ N 17  Тема: Статическая неопределимость. Степень статической неопределенности Связи, обеспечивающие кинематическую неизменяемость системы, называются …

			необходимыми
			дополнительными (линейными)
			абсолютно жесткими
			упругими

Решение: На балку наложены три линейные связи (рис. 1). При отбрасывании одной из них балка становится кинематически изменяемой. (рис. 2, 3, 4). Следовательно, все связи являются необходимыми.

 ЗАДАНИЕ N 18  Тема: Расчет простейших статически неопределимых систем На рисунке показана балка нагруженная моментами М. Эпюра изгибающих моментов имеет вид …

 ЗАДАНИЕ N 19  Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина Для данной расчетной схемы формула интеграла Мора имеет вид …

 ЗАДАНИЕ N 20  Тема: Метод сил 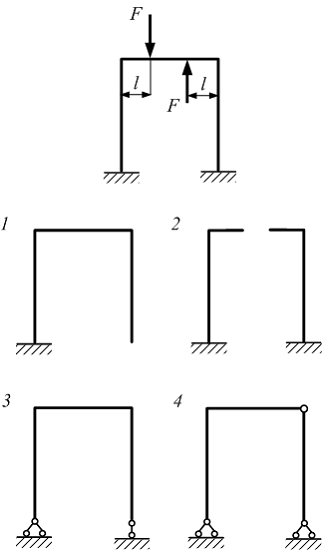На рисунке показана три раза статически неопределимая и симметричная в геометрическом отношении рама. Внешняя нагрузка кососимметрична. Рациональный вариант основной системы показан на рисунке …

			2
			1
			3
			4

  ЗАДАНИЕ N 21  Тема: Моменты инерции простых и сложных сечений 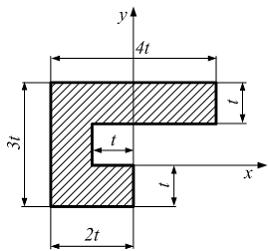Центробежный момент инерции фигуры относительной осей x, y равен ____ 

Решение: 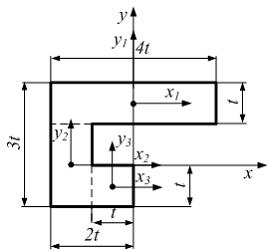Делим фигуру на три прямоугольника и используем формулу параллельного переноса

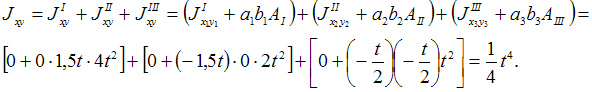
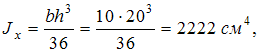
  ЗАДАНИЕ N 22  Тема: Главные оси и главные моменты инерциим Моменты инерции треугольника относительно осей x и y, проходящих через центр тяжести поперечного сечения, параллельно катетам: Положение главных центральных осей определяется углом   а главные центральные моменты инерции равны 

Решение: 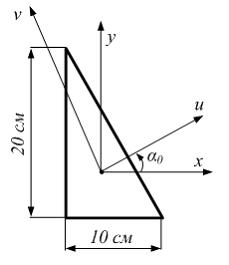Положение главных центральных осей определяем по формуле 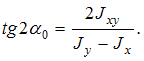 Подставляя числовые значения, получаем  Так как   откладываем его от положительного направления оси x против часовой стрелки. Главные центральные моменты инерции определяем по формуле 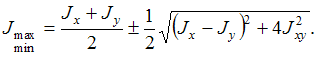После подстановки числовых значений имеем Из расположения площади треугольника относительно осей u и v следует, что   а 

  ЗАДАНИЕ N 23  Тема: Статические моменты. Центр тяжести плоской фигуры 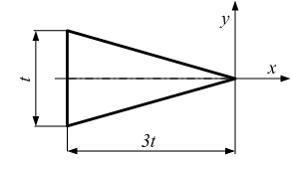Статический момент площади треугольника относительно оси y в заданной системе координат равен …

Решение: где   – координата центра тяжести треугольника.

 ЗАДАНИЕ N 24  Тема: Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей 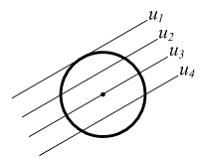Осевой момент инерции круга принимает минимальное значение относительно оси …

  ЗАДАНИЕ N 25  Тема: Формула Эйлера для критической силы сжатого стержня и пределы ее применимости Стержень квадратного сечения со стороной b сжимается силой F. При замене сечения на прямоугольное шириной 2b и высотой   при прочих равных условиях, значение критической силы … При решении учитывать, что напряжения в сжатом стержне не превышают предел пропорциональности.

			уменьшится в 4 раза
			не изменится
			увеличится в 4 раза
			уменьшится в 2 раза

Решение: При напряжениях меньше предела пропорциональности для определения критической силы сжатого стержня используют формулу Эйлера Изменение формы и размеров поперечного сечения, при прочих равных условиях учитывается через минимальный момент инерции сечения  Для квадратного сечения 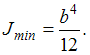Для прямоугольного сечения с размерами 2b и  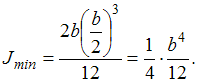Следовательно, значение критической силы уменьшится в четыре раза.

 ЗАДАНИЕ N 26  Тема: Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость    Стержень длиной   сжат силой F. Схема закрепления показана на рисунке а. Зависимость критического напряжения от гибкости для материала Ст. 3 приведена на рисунке б. Поперечное сечение швеллер №10. Площадь поперечного сечения  радиусы инерции    Значение критической силы равно ____ кН.

			247
			124
			318
			212

  ЗАДАНИЕ N 27  Тема: Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня Стержень длиной l круглого сечения диаметром d сжимается силой F. Напряжения в стержне не превышают предела пропорциональности. При увеличении диаметра в два раза, при прочих равных условиях, критическое напряжение ____________ раза.

			увеличится в 4
			увеличится в 2
			уменьшится в 2
			уменьшится в 4

Решение: Критическое напряжение в сжатом стержне, если напряжение в стержне не превышает предела пропорциональности, определяется по формуле  где    Для круглого стержня  При увеличении диаметра в два раза  Следовательно, при увеличении диаметра стержня в два раза критическое напряжение увеличится в четыре раза.

  ЗАДАНИЕ N 28  Тема: Влияние условий закрепления концов стержня на величину критической силы Схема закрепления стержня длиной l показана на рисунке. При удалении промежуточной опоры в середине пролета значение критического напряжения … При решении учитывать, что напряжения в сжатых стержнях не превышают предел пропорциональности.

			уменьшится в 4 раза
			не изменится
			увеличится в 4 раза
			уменьшится в 2 раза

Решение: Для определения критического напряжения, когда напряжения в сжатом стержне не превышают предел пропорциональности, используем формулу 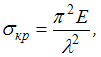 где 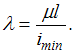 Коэффициент приведения длины   учитывает условия закрепления стержня. До удаления опоры   после удаления –  Следовательно, значение критического напряжения после удаления опоры, уменьшится в четыре раза.

  ЗАДАНИЕ N 29  Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) После определения величин главных напряжений им присваивают индексы 1, 2, 3, исходя из условия …

Решение: Главным напряжениям присваивают индексы 1, 2, 3 так, чтобы выполнялось условие 

 ЗАДАНИЕ N 30  Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности Классические теории прочности: 1) теория наибольших нормальных напряжений, 2) теория наибольших линейных деформаций удлинения, 3) теория наибольших касательных напряжений, 4) теория удельной потенциальной энергии формоизменения. Для оценки прочности пластичных материалов используются _____ теории прочности.

			3 и 4
			1 и 4
			2 и 3
			1 и 2

  ЗАДАНИЕ N 31  Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Совокупность линейных       и угловых       деформаций элементарного прямоугольного параллелепипеда в произвольной системе координат xyz называется …

			тензором деформированного состояния
			напряженным состоянием
			деформированным состоянием
			тензором напряженного состояния

Решение: Три линейные и три угловые деформации (     ,      ) элементарного прямоугольного параллелепипеда в произвольной системе координат xyz образуют тензор деформированного состояния.

  ЗАДАНИЕ N 32  Тема: Виды напряженного состояния 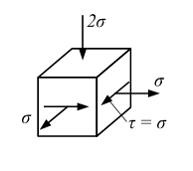На рисунке показан элементарный параллелепипед и напряжения на его гранях. Напряженное состояние …

			плоское (чистый сдвиг)
			линейное (одноосное растяжение)
			линейное (одноосное сжатие)
			объемное

Решение: Верхняя грань элементарного параллелепипеда является главной площадкой с главным напряжением равным   Два других главных напряжения определим по формуле  где:     (см. рисунок, вид сверху на элементарный параллелепипед). Подставляя в формулу значения напряжений, получаем  Присваивая главным напряжениям индексы, имеем:     

Напряженное состояние плоское (чистый сдвиг).

(13)

  ЗАДАНИЕ N 1 Тема: Продольная сила. Напряжения и деформации Отношение значений продольных сил в сечениях С-С и К-К (см. рисунок) равно …

			1
			–1

Решение: Оба сечения принадлежат одному грузовому участку. Величина продольной силы не зависит от площади поперечного сечения. Поэтому отношение 

  ЗАДАНИЕ N 2  Тема: Механические свойства и механические характеристики материалов Большинство пластичных материалов при испытаниях на растяжение и сжатие …

			ведут себя одинаково вплоть до предела текучести
			лучше работают на сжатие, чем на растяжение
			лучше работают на растяжение, чем на сжатие
			ведут себя одинаково вплоть до предела прочности

Решение: Большинство пластичных материалов при испытаниях на растяжение и сжатие ведут себя одинаково вплоть до предела текучести.

 ЗАДАНИЕ N 3  Тема: Расчеты стержней на прочность и жесткость 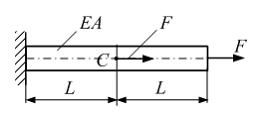На рисунке показан стержень, загруженный двумя силами F.   – допустимое перемещение сечения С задано. Величины: Е, А, L – известны. Максимально допустимое значение силы F равно …

  ЗАДАНИЕ N 4  Тема: Испытание конструкционных материалов на растяжение и сжатие 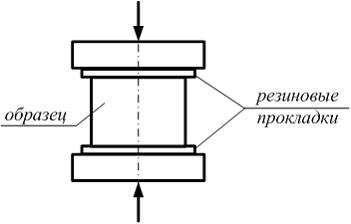При испытании образца на сжатие (см. рисунок) между образцом и плитами испытательной машины устанавливаются резиновые прокладки с целью …

			уменьшения сил трения между поверхностями образца и поверхностями плит испытательной машины
			уменьшения шума при разрушении образца
			увеличения величины поперечной деформации
			резкого уменьшения высоты образца до момента разрушения

Решение: Резиновые прокладки устанавливаются для уменьшения сил трения между поверхностями образца и поверхностями плит испытательной машины.

  ЗАДАНИЕ N 5  Тема: Статическая неопределимость. Степень статической неопределенности 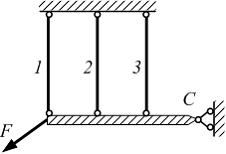Степень статической неопределимости системы (см. рисунок) равна …

			двум
			единице
			трем
			четырем

Решение: 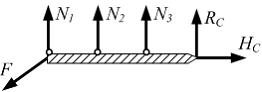На горизонтальный заштрихованный элемент действуют шесть сил (см. рисунок), пять из которых   неизвестны. Для данной системы сил можно составить три уравнения равновесия. Следовательно, система два раза статически неопределима.

  ЗАДАНИЕ N 6  Тема: Расчет простейших статически неопределимых систем На рисунке показан стержень нагруженный силами F и моментами М. Размер l, диаметр d, модули упругости Е и G заданы. Крутящий момент и продольная сила в сечении С-С, соответственно, равны …

			0, 0

Решение: Стержень геометрически симметричен относительно плоскости симметрии С-С. Нагрузим стержень поочередно моментами М и силами F (рис. 1, 2). В первом варианте (рис. 1) стержень нагружен симметричной нагрузкой. Следовательно в сечении С-С кососимметричный внутренний силовой фактор, крутящий момент, равен нулю. Во втором варианте (рис. 2) стержень  нагружен кососимметричной нагрузкой. Следовательно, в сечении С-С симметричный внутренний силовой фактор, продольная сила, равен нулю. Таким образом, в сечении С-С и во всех сечениях среднего грузового участка крутящий момент и продольная сила равны нулю.

  ЗАДАНИЕ N 7  Тема: Метод сил Результат умножения симметричной эпюры на кососимметричную – …

			ноль
			положительное число
			отрицательное число
			число положительное и отрицательно

Решение: На рисунке показаны симметричная и кососимметричная эпюры. Буквами   и   обозначены центры тяжестей площадей   и   Перемножим площади   на ординаты   и сложим произведения. Получим нулевой результат.

 ЗАДАНИЕ N 8  Тема: Определение перемещений с помощью интегралов Мора. Правило Верещагина При плоском изгибе, без учета поперечных сил, интеграл Мора вычисляется способом Верещагина по формуле 

  ЗАДАНИЕ N 9  Тема: Виды напряженного состояния Стальной кубик вставлен без зазора в жесткую обойму (см. рис.). На верхнюю грань кубика действует равномерно распределенное давление интенсивности р. Поверхности кубика и обоймы абсолютно гладкие. Напряженное состояние кубика показано на рисунке …

			в
			г
			б
			а

Решение: Силы трения между абсолютно гладкими поверхностями кубика и обоймы отсутствуют. Поэтому касательные напряжения на гранях кубика равны нулю, и все грани являются главными площадками. В процессе сжатия ребра кубика, направленные вдоль осей x и y, стремятся удлиниться. Удлинение вдоль оси y происходит свободно. Удлинение вдоль оси x невозможно (мешает жесткая обойма). В связи с невозможностью удлинения вдоль оси x, со стороны вертикальных плоскостей обоймы на кубик действуют усилия в виде равномерно распределенных по площади нагрузок с некоторой интенсивностью  . Интенсивности р и   следует рассматривать как главные напряжения. Таким образом, из трех главных напряжений одно   (по фронтальной грани кубика). Поэтому напряженное состояние кубика плоское (рис. в).

  ЗАДАНИЕ N 10  Тема: Деформированное состояние в точке. Связь между деформациями и напряжениями Стержень растянут усилиями, равномерно распределенными по его торцам с интенсивностью р. Модуль упругости Е и коэффициент Пуассона   материала стержня известны. Относительное изменение объема стержня равно …

Решение: 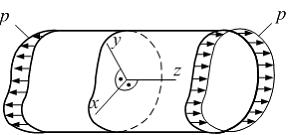Так как напряженное состояние стержня однородное, то относительное изменение объема не зависит от формы и размеров стержня и определяется по формуле   где   − линейные деформации в трех произвольных, взаимно перпендикулярных направлениях, проходящих через произвольную точку стрежня. В данном случае деформации   легко вычислить, если одно направление   выбрать параллельным оси стержня, а два других (y и x) расположить в плоскости поперечного сечения. Далее используем формулу закона Гука   и выражение для коэффициента Пуассона   откуда    Подставляя значения   в формулу для   получаем 

 ЗАДАНИЕ N 11  Тема: Оценка прочности материала при сложном напряженном состоянии. Теории прочности На рисунке показано напряженное состояние в точке. Материал пластичный с пределом текучести   Для перехода материала из упругого состояния в пластичное компоненты напряженного состояния следует увеличить в _____ раз(-а). Использовать теорию наибольших касательных напряжений.

			4,5
			9
			3
			5,3

  ЗАДАНИЕ N 12  Тема: Напряженное состояние в точке. Главные площадки и главные напряжения) После определения величин главных напряжений им присваивают индексы 1, 2, 3, исходя из условия …

Решение: Главным напряжениям присваивают индексы 1, 2, 3 так, чтобы выполнялось условие 

 ЗАДАНИЕ N 13  Тема: Основные понятия, определения, допущения и принципы Свойство материала сохранять некоторую часть деформации после снятия нагрузки называется …

			пластичностью
			упругостью
			жесткостью
			твердостью

  ЗАДАНИЕ N 14  Тема: Модели прочностной надежности Первым этапом при расчете конструкции является …

			выбор расчетной схемы
			определение реакций опор
			составление условия прочности
			построение эпюр внутренних силовых факторов

Решение: Рассчитать конструкцию с учетом всех ее свойств не представляется возможным в виду их очевидной неисчерпаемости. Поэтому конструкция освобождается от свойств, несущественных при решении данной задачи. Таким образом, осуществляется переход от реального объекта к расчетной схеме. Затем расчетная схема анализируется с помощью аппарата сопротивления материалов.

 ЗАДАНИЕ N 15  Тема: Перемещение и деформация Точка К принадлежит деформируемому телу и перемещается в плоскости xoy (см. рисунок). Полное перемещение точки   Перемещение вдоль оси x   Перемещение вдоль оси y равно ___ мм.

			4
			2
			8

  ЗАДАНИЕ N 16  Тема: Внутренние силы и напряжения В процессе нагружения тела внешними силами между частицами материала возникают дополнительные внутренние силы, которые …

			являются предметом изучения в сопротивлении материалов
			не являются предметом изучения в сопротивлении материалов
			являются предметом изучения в сопротивлении материалов при небольших внешних нагрузках
			не являются предметом изучения в сопротивлении материалов, если тело находится в покое

Решение: Дополнительные внутренние силы, возникающие между частицами материала, в процессе нагружения тела внешней нагрузкой являются предметом изучения в сопротивлении материалов.

 ЗАДАНИЕ N 17  Тема: Главные оси и главные моменты инерции Главными центральными осями для круга являются оси(ось) …

			2-2, 3-3
			2-2
			1-1, 3-3
			4-4, 2-2

  ЗАДАНИЕ N 18  Тема: Моменты инерции простых и сложных сечений Момент инерции равнобедренного треугольника относительно оси x, проходящей через центр тяжести параллельно основанию, равен …

Решение: Момент инерции определяем по формуле для треугольника 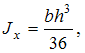 где    Подставляя значения b и h в формулу, получаем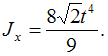 

  ЗАДАНИЕ N 19  Тема: Статические моменты. Центр тяжести плоской фигуры Площадь фигуры   Статические моменты площади:    Координаты центра тяжести фигуры   

			–1,5; 3,5
			1,5; 3,5
			2; 4
			0,29; –0,67