52

Министерство образования Российской Федерации

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра теории авиационных и ракетных двигателей

РАСЧЕТ ГИДРАВЛИЧЕСКОЙ СЕТИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к курсовой работе по дисциплинам “Механика жидкости и газа” и “Прикладная гидрогазовая динамика” для студентов направления 550900 – Теплоэнергетика и специальностей 131500 - Авиационная и ракетно-космическая теплотехника и 100500 - Тепловые электрические станции

Уфа 2002

Составитель: А.Н. Гришин

УДК 532 (075.8)

Расчет гидравлической сети: Методические указания к курсовой работе по дисциплинам «Механика жидкости и газа» и «Прикладная гидрогазовая динамика» для студентов направления 550900 Теплоэнергетика и специальностей 131500 – Авиационная и ракетно-космическая теплотехника и 100500 - Тепловые электрические станции / Уфимск. гос. авиац. техн. унив-т; Сост. А.Н. Гришин. - Уфа, 2002. – 53 с.

Методические указания содержат сведения о расчете простого и сложного трубопроводов, а также трубопроводов с насосной подачей. Приведен пример расчета гидравлической сети. Разработаны варианты заданий по расчету гидравлической сети. Сформулированы основные требования к оформлению пояснительной записки по курсовой работе.

Табл. - 4 Ил. - 18 Библиогр. - 5 назв.

Рецензенты: докт. техн. наук, проф. В.А. Трушин

канд. техн. наук, доц. Ф.Ф. Тарасов.

Содержание

Введение 5

1. Цель работы 6

Теоретические основы 6

1. .1 Уравнение Бернулли для несжимаемой вязкой жидкости в канале 6

2.2 Ламинарное и турбулентное течение вязкой несжимаемой

жидкости в трубе 7

2.3 Полуэмпирический логарифмический закон распределения

скорости в трубе 11

2.4 Степенной эмпирический закон распределения скорости 15

2.5 Законы сопротивления гладких труб 16

2.6 Течение жидкости в шероховатых трубах 17

2.7 Гидравлическое сопротивление труб с некруглым поперечным

сечением 20

2.8 Гидравлические потери – потери трения и местные потери 20

2.9 Местные сопротивления при ламинарном и турбулентном

режимах течения 23

2.10 Эквивалентная длина трубопровода. Удельные линейные

потери давления 24

2.11 Местные гидравлические сопротивления – потери при

внезапном расширении и сужении трубы, потери в отводах,

потери при слиянии и разделении потоков 26

Расчет гидравлической сети 29

1. Принцип наложения потерь при расчете гидравлической сети 29

2. Простой трубопровод. Порядок расчета простого трубопровода 30

3. Сложный трубопровод. Последовательное и параллельное

соединение трубопроводов. Разветвленный трубопровод 33

3.4 Трубопровод с насосной подачей 36

3. Содержание и порядок выполнения работы 39

   1. Бланк задания 39

   2. Порядок гидравлического расчета 43

4. Требования к оформлению работы 47

Список литературы 48

Приложения 49

Введение

Гидравлические сети находят широкое применение в технике. В качестве примера можно привести водопроводные, газовые, паровые, нефтепроводные и другие сети. Наиболее сложной сетью с упругими стенками труб является кровеносная система сосудов человека.

Гидравлические сети применяют для транспортировки жидкостей и газов. Например, топливная система двигателя подает топливо из бака в камеру сгорания, система смазки обеспечивает доставку масла к подшипникам двигателя и т.д.

Гидравлическая сеть, в общем случае, состоит из множества трубопроводов различного сечения, связывающих разные местные сопротивления друг с другом. В состав сети в качестве источника энергии входят, как правило, насос или компрессор.

Гидравлические сети любой сложности можно заменить эквивалентной схемой, представляющей совокупность местных сопротивлений, моделирующих все сопротивления этой сети. Вся совокупность местных сопротивлений разбивается на ветви или простые трубопроводы. Методика расчета сети зависит от методики расчета простых и сложных трубопроводов, образующих сеть.

Выполнив расчет гидравлической сети, студенты получат навыки при решении задач, связанных с транспортировкой жидкостей с помощью трубопроводов.

1. Цель работы

Целью работы являются:

• изучение методов расчета простого трубопровода;

• изучение методов расчета сложного трубопровода;

• изучение методов расчета трубопроводов с насосной подачей;

• изучение методов расчета гидравлической сети;

• получение навыков расчета гидравлической сети.

2. Теоретические основы

2.1 Уравнение Бернулли для несжимаемой вязкой жидкости в канале

Рассмотрим течение несжимаемой вязкой жидкости в горизонтальном канале, полагая его близким к одномерному, когда v w 0. В этом случае уравнение Навье-Стокса имеет вид:

(2.1)

где = - оператор Лапласа; F_x = F_y=0, F_z = -g – проекции массовой силы.

Из последнего уравнения в (2.1) найдем:

. (2.2)

Этот результат позволяет перейти от уравнения Бернулли для струйки тока к аналогичному уравнению, справедливому для всего потока в канале. Для этого произведем осреднение параметров жидкости по расходу в двух сечениях канала:

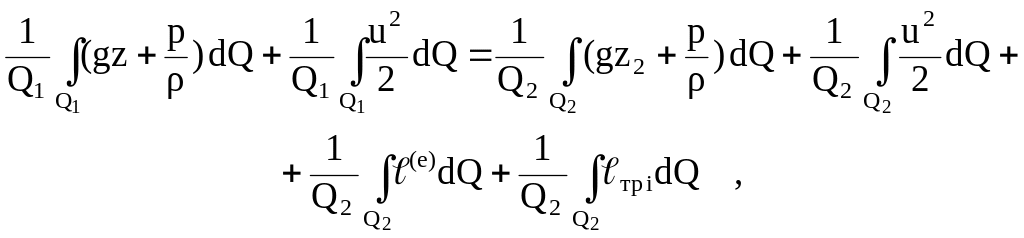
где Q₁ = Q₂ = Q – объемный расход жидкости; ^(e) – удельная внешняя (по отношению к струйке) работа; _{тр i} – удельная работа трения, переходящая в теплоту трения (_{тр i} = q_{тр i}).

С учетом (2.2) полученное уравнение преобразуем к виду:

(2.3)

где u₁, u₂ – среднерасходные скорости ( );

- коэффициент Кориолиса ( );

_тех – техническая работа ( );

_тр – работа трения ( ).

2. Ламинарное и турбулентное течения вязкой несжимаемой жидкости в трубе

На рисунке 2.1 изображена картина течения при ламинарном режиме движения жидкости в трубе. В начале трубы имеется ядро с безвихревым течением. Участок течения, где существует ядро, называется начальным (входным, участком гидродинамической стабилизации). Его длина у разных авторов изменяется в пределах: _н /d = 0,03Re (по Шиллеру), _н /d = 0,04Re (по Таргу), _н /d = 0,065Re (по Буссинеску), где Re = ud/.

Течение в начальном участке может быть рассчитано на основе теории пограничного слоя.

Поле скорости на основном участке находится из решения уравнения Навье-Стокса. В [1], [2] приведено такое решение для трубы эллиптического сечения. С учетом граничного условия уравнение Навье-Стокса преобразуется в уравнение Пуассона:

(2.4)

где u – проекция скорости на ось трубы (v = w = 0); p/  – падение давления на участке длиной 1м;  – длина трубы.

Решение уравнения (2.4) имеет вид [1], [2]:

где u_m – скорость на оси трубы; a – длина большой полуоси эллипса; r – текущий радиус.

В частном случае трубы круглого сечения (а = R) распределение скоростей описывается параболой:

, (2.5)

где (2.6)

u_ср – среднерасходная скорость.

В технике потери давления определяют по формуле Дарси-Вейсбаха:

(2.7)

где  - коэффициент гидросопротивления трубы на участке длиной в один калибр.

Выразив p через u_ср с помощью (2.6), получим для трубы круглого сечения закон сопротивления Пуазейля:

(2.8)

где .

Подставив (2.8) в (2.7), найдем:

(2.9)

Следовательно, в трубе круглого сечения при ламинарном течении сопротивление движению пропорционально скорости в первой степени. Можно показать, что этот вывод справедлив и для труб плоского и эллиптического сечений [1].

Распределение скорости в трубе характеризуется большой неравномерностью. Коэффициент Кориолиса для ламинарного течения равен  = 2.

При числах Рейнольдса больших критического значения Re_кр=2200 – 2300 в трубе наблюдается турбулентное течение. Длина начального участка значительно короче, чем при ламинарном течении. На рисунке 2.2 изображены начальный и основной участки.

По измерениям Кирстена _н /d = 50 – 100. Никурадзе получил _н /d = 25 – 40. В длинных трубах длиной начального участка часто пренебрегают. В коротких трубах потери давления в начальном участке определяют по формуле Вейсбаха:

(2.10)

где _Н – эмпирический коэффициент сопротивления.

При турбулентном режиме течения отсутствует теоретическое решение уравнений Навье-Стокса. Поэтому при решении практических задач часто поле скорости задают либо полуэмпирическими, либо эмпирическими зависимостями.

Эксперименты показывают, что безразмерные профили скорости в различных сечениях основного участка трубы совпадают друг с другом при их наложении. Поэтому можно записать:

(2.11)

где f (r/R)-функция безразмерного текущего радиуса.

Используя (2.11) , найдем расход жидкости:

(2.12)

где S-площадь сечения трубы.

Видно, что при постоянной площади сечения трубы скорость на оси трубы постоянна, то есть .

Р ассмотрим контрольную поверхность радиуса r и длиной  на рисунке 2.3.

При отсутствии массовых сил на жидкость действует сила:

где S_п - площадь проницаемых поверхностей.

Проекция силы на ось х будет равна:

Согласно (2.11) и (2.12) скорости u₁ и u₂ не зависят от координаты х. Поэтому последнее выражение примет вид:

(2.13)

Так как R_x=П, где П - периметр сечения трубы, то из (2,13) найдем:

(2.14)

Используя (2.14), найдем напряжение трения, действующее на жидкость на стенке (при y=0):

. (2.15)

Из (2.14) и (2.15) получим линейный закон изменения касательных напряжений в трубе:

(2.16)

Эта формула справедлива как для турбулентного, так и для ламинарного режима течения (при ламинарном режиме также справедлива формула (2.11)).