
- •Общая теория статистики
- •Глава 1. Понятие о статистике................. 13
- •Глава 2. Организация статистики. Статистическое наблюдение ...... 32
- •Глава 3. Статистические показатели ............. 82
- •Глава 4. Представление статистических данных: таблицы и графики. 100
- •Глава 5. Средние величины и изучение вариации. ... 120
- •Глава 6. Группировка........................ 172
- •Глава 7. Выборочное наблюдение. Испытание статистических гипотез .. 214
- •Глава 8. Статистическая проверка гипотез........ 270
- •Глава 9. Корреляционно-регрессионный анализ и моделирование статистических связей . . . 320
- •Глава 10. Системы регрессионных уравнений....... 392
- •Глава 11. Статистический анализ неколичественных переменных . 411
- •Глава 12. Статистическое изучение динамики....... 445
- •Глава 13. Индексы ........................... 526
- •Глава 14. Статистическое изучение структуры совокупности и ее изменений ... 597
- •Предисловие
- •Глава 1. Понятие о статистике
- •1.1. Что такое статистика
- •1.2. Статистическая закономерность. Статистические совокупности
- •1.3. Признаки и их классификация
- •1.4. Определение предмета статистики — основа статистической методологии
- •Рекомендуемая литература
- •2 Глава. Организация статистики. Статистическое наблюдение
- •2.1. Организация государственной статистики в Российской Федерации
- •2.2. Важнейшие международные организации и их статистические службы
- •2.3. Требования, предъявляемые к собираемым данным. Формы организации и виды статистического наблюдения
- •2.4. Подготовка статистического наблюдения
- •2.5. Статистическая отчетность
- •2.6. Ошибки статистического наблюдения. Методы контроля данных наблюдения
- •2.7. Реформирование российской государственной Статистики
- •Рекомендуемая литература
- •3. Глава. Статистические показатели
- •3.1. Сущность и значение статистических показателей.
- •3.2. Классификация статистических показателей
- •3.3. Общие принципы построения относительных статистических показателей
- •3.4. Понятие о системах статистических показателей
- •3.5. Функции статистических показателей
- •Рекомендуемая литература
- •4 Глава. Представление статистических данных: таблицы и графики
- •4.1. Статистические таблицы
- •4.2. Основные виды графиков
- •4.3. Картограммы и картодиаграммы
- •Рекомендуемая литература
- •5 Глава. Средние величины и изучение вариации
- •5.1. Однородность и вариация массовых явлений
- •5.2. Средняя арифметическая величина
- •5.3. Другие формы средних величин
- •5.4. Средняя величина как выражение закономерности
- •5.5. Вариация массовых явлений
- •5.6. Построение вариационного ряда. Виды рядов. Ранжирование данных
- •5.7. Структурные характеристики вариационного ряда
- •5.8. Показатели размера и интенсивности вариации
- •5.9. Моменты распределения и показатели его формы
- •5.10. Предельно возможные значения показателей вариации и их применение
- •Рекомендуемая литература
- •6 Глава. Группировка
- •6.1. Значение и сущность группировки
- •6.2. Виды группировок
- •6.3. Многомерные группировки
- •Рекомендуемая литература
- •7 Глава. Выборочное наблюдение. Испытание статистических гипотез
- •7.1. Причины применения выборочного наблюдения. Дескриптивная статистика и статистический вывод
- •7.2. Способы отбора, обеспечивающие репрезентативность выборки. Виды выборки
- •7.3. Ошибка выборки
- •7.4. Влияние вида выборки на величину ошибки выборки
- •7.5. Задачи, решаемые при применении выборочного метода
- •7.6. Распространение данных выборочного наблюдения на генеральную совокупность
- •7.7. Малая выборка
- •7.8. Примеры применения выборочного метода
- •Рекомендуемая литература
- •8 Глава. Статистическая проверка гипотез
- •8.1. Общие понятия
- •8.2. Проверка гипотезы о законе распределения
- •8.3. Проверка гипотезы о связи на основе критерия x2 (хи-квадрат)
- •8.4. Проверка гипотезы о средних величинах
- •8.5. Основы дисперсионного анализа
- •8.6. Некоторые непараметрические критерии
- •Рекомендуемая литература
- •9 Глава. Корреляционно-регрессионный анализ и моделирование статистических связей
- •9.1. Понятие о статистической и корреляционной связи
- •9.2. Условия применения и ограничения корреляционно-регрессионного метода
- •9.3. Задачи корреляционно-регрессионного анализа и моделирования
- •3. Задана прогнозирования возможных значений результативного признака при задаваемых значениях факторных признаков.
- •9.4. Вычисление и интерпретация параметров парной линейной регрессии
- •9.5. Статистическая оценка надежности параметров парной регрессии и корреляции
- •9.6. Применение линейного уравнения парной регрессии
- •9.7. Вычисление параметров парной линейной регрессии на основе аналитической группировки
- •9.8. Параболическая корреляция
- •9.9. Гиперболическая корреляция
- •9.10. Множественное уравнение регрессии
- •9.11. Меры тесноты связей в многофакторной системе
- •9.13. Корреляционно-регрессионные модели и их применение в анализе и прогнозе
- •Рекомендуемая литература
- •10 Глава. Системы регрессионных уравнений
- •10.1. Понятие о системах регрессионных уравнений
- •10.2. Проблемы решения систем взаимосвязанных уравнений
- •10.4. Косвенный метод наименьших квадратов
- •10.5. Двойной метод наименьших квадратов
- •Рекомендуемая литература
- •11 Глава. Статистический анализ неколичественных переменных
- •11.1. Зависимость методов измерений связей от уровня измерения переменных
- •11.2. Измерение связи между двумя дихотомическими переменными
- •11.5. Другие меры связей между номинальными переменными
- •11.6. Коэффициенты корреляции рангов
- •Рекомендуемая литература
- •12 Глава. Статистическое изучение динамики
- •12.1. Виды динамических рядов. Сопоставимость данных в изучении динамики
- •12.2. Элементы динамики: основная тенденция и колебания
- •12.3. Показатели, характеризующие тенденцию динамики
- •12.4. Особенности показателей динамики для рядов, состоящих из относительных уровней
- •12.5. Средние показатели тенденции динамики
- •12.6. Методы выявления типа тенденции динамики
- •12.7. Методика измерения параметров тренда
- •12.8. Методика изучения и показатели колеблемости
- •12.9. Измерение устойчивости в динамике
- •12.10. Сезонные колебания и полное разложение дисперсии уровней динамического ряда
- •12.11. Прогнозирование на основе тренда и колеблемости
- •12.12. Корреляция рядов динамики
- •Рекомендуемая литература
- •13 Глава. Индексы
- •13.1. Понятие индекса
- •13.2. Индекс как показатель центральной тенденции (индекс средний из индивидуальных)
- •13.3. Агрегатные индексы. Система индексов
- •13.4. Свойства индексов
- •13.5. Индексный анализ взвешенной средней. Индекс структуры
- •13.6. Построение индексов при обобщении данных по единицам совокупности и по элементам
- •13.7. Границы и условия применения индексного метода
- •13.8. Комплексное использование индексного и регрессионного методов анализа
- •13.9. Примеры использования индексов в экономико-статистических расчетах
- •Рекомендуемая литература
- •14 Глава. Статистическое изучение структуры совокупности и ее изменений
- •14.1. Показатели простой (одномерной) структуры
- •14.2. Показатели иерархической (древовидной) структуры
- •14.3. Показатели балансовой структуры
- •14.4. Показатели многомерной структуры с пересекающимися признаками
- •14.6. Показатели концентрации, специализации, монополизации. Многомерная структура
- •14.7. Абсолютные и относительные показатели изменения структуры
- •14,8. Ранговые показатели изменения структуры
- •Рекомендуемая литература
- •Приложения
- •1. Статистико-математические таблицы
- •2. Основные принципы официальной статистики в регионе Европейской экономической комиссии
9.13. Корреляционно-регрессионные модели и их применение в анализе и прогнозе
Корреляционно-регрессионной моделью (КРМ) системы взаимосвязанных признаков является такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака, обладает высоким (не ниже 0,5) коэффициентом детерминации и коэффициентами регрессии, интерпретируемыми в соответствии с теоретическим знанием о природе связей в изучаемой системе.
Приведенное определение КРМ включает достаточно строгие условия: далеко не всякое уравнение регрессии можно считать моделью. В частности, полученное выше по 16 хозяйствам уравнение не отвечает последнему требованию из-за противоречащего экономике сельского хозяйства знака при факторе х2 — доля пашни. Однако в учебных целях будем рассматривать его как модель.
Теория и практика выработали ряд рекомендаций для построения корреляционно-регрессионной модели.
382
1. Признаки-факторы должны находиться в причинной связи с результативным признаком (следствием). Поэтому недопустимо, например, в модель себестоимости у вводить в качестве одного из факторов xj коэффициент рентабельности, хотя включение такого «фактора» значительно повысит коэффициент детерминации.
2. Признаки-факторы не должны быть составными частями результативного признака или его функциями.
3. Признаки-факторы не должны дублировать друг друга, т.е. быть коллинеарными (с коэффициентом корреляции более 0,8). Так, не следует в модель производительности труда включать энерго- и фондовооруженность рабочих, поскольку эти факторы тесно связаны друг с другом в большинстве объектов.
4. Не следует включать в модель факторы разных уровней иерархии, т.е. фактор ближайшего порядка и его субфакторы. Например, в модель себестоимости зерна не следует включать и урожайность зерновых культур, и дозу удобрений под них или затраты на обработку гектара, показатели качества семян, плодородия почвы, т.е. субфакторы самой урожайности.
5. Желательно, чтобы для результативного признака и факторов соблюдалось единство единицы совокупности, к которой они отнесены. Например, если у — валовой доход предприятия, то и все факторы должны относиться к предприятию: стоимость производственных фондов, уровень специализации, численность работников и т.д. Если же у — средняя зарплата рабочего на предприятии, то факторы должны относиться к рабочему: разряд или классность, стаж работы, возраст, уровень образования, энерговооруженность и т.д. Правило это некатегорическое, в модель заработной платы рабочего можно включить, к примеру, и уровень специализации предприятия. Вместе с тем нельзя забывать о предыдущей рекомендации.
6. Математическая форма уравнения регрессии должна соответствовать логике связи факторов с результатом в реальном объекте. Например, такие факторы урожайности, как дозы разных удобрений, уровень плодородия, число прополок и т.п., создают прибавки величины урожайности, малозавися-Аше друг от друга; урожайность может существовать и без любого из этих факторов. Такому характеру связей отвечает аддитивное уравнение регрессии:
![]() 383
383
 Первое
слагаемое в правой части равенства —
это отклонение, которое возникает за
счет отличия индивидуальных значений
факторов у данной единицы совокупности
от их средних значений по совокупности.
Его можно назвать эффектом
факторообеспеченности. Второе слагаемое
— отклонение, которое возникает за счет
не входящих в модель факторов и отличия
индивидуальной эффективности факторов
у данной единицы совокупности от средней
эффективности факторов в совокупности,
измеряемой коэффициентами ус-
Первое
слагаемое в правой части равенства —
это отклонение, которое возникает за
счет отличия индивидуальных значений
факторов у данной единицы совокупности
от их средних значений по совокупности.
Его можно назвать эффектом
факторообеспеченности. Второе слагаемое
— отклонение, которое возникает за счет
не входящих в модель факторов и отличия
индивидуальной эффективности факторов
у данной единицы совокупности от средней
эффективности факторов в совокупности,
измеряемой коэффициентами ус-
384
Таблица 9.12 Анализ факторообеспеченности и фактороотдачи по регрессионной модели уровня валового дохода
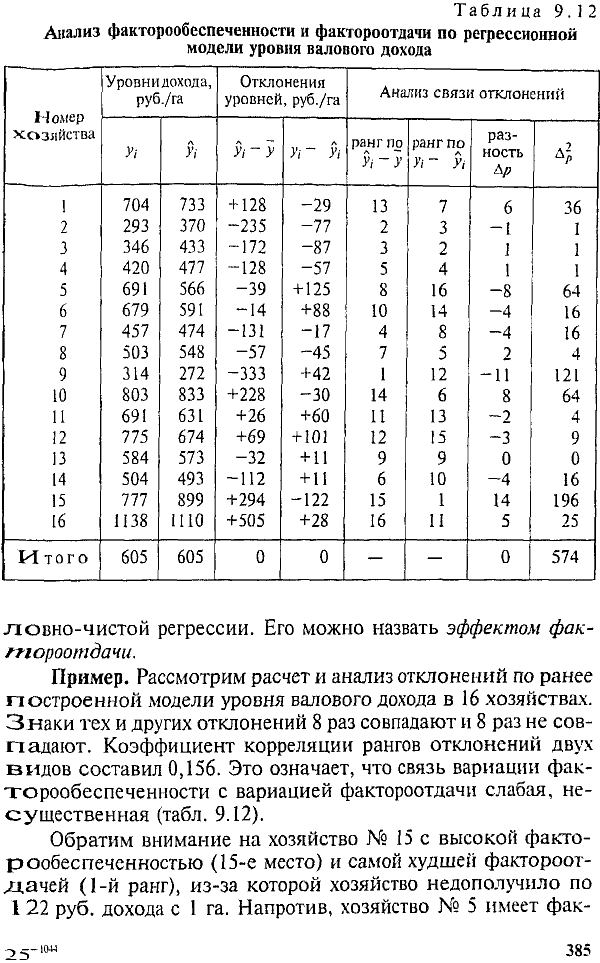 ловно-чистой
регрессии. Его можно назвать эффектом
фактороотдачи.
ловно-чистой
регрессии. Его можно назвать эффектом
фактороотдачи.
Пример. Рассмотрим расчет и анализ отклонений по ранее построенной модели уровня валового дохода в 16 хозяйствах. Знаки тех и других отклонений 8 раз совпадают и 8 раз не совпадают. Коэффициент корреляции рангов отклонений двух видов составил 0,156. Это означает, что связь вариации факторообеспеченности с вариацией фактороотдачи слабая, несущественная (табл. 9.12).
Обратим внимание на хозяйство № 15 с высокой факто-
рообеспеченностью (15-е место) и самой худшей фактороот-
дачей (1-й ранг), из-за которой хозяйство недополучило по
1 22 руб. дохода с 1 га. Напротив, хозяйство № 5 имеет фак-
385
торообеспеченность ниже средней, но благодаря более эффективному использованию факторов получило на 125 руб. дохода с 1 га больше, чем было бы получено при средней по совокупности эффективности факторов. Более высокая эффективность фактора х\ (затраты труда) может означать более высокую квалификацию работников и большую заинтересованность в качестве выполняемой работы. Более высокая эффективность фактора хз с точки зрения доходности может заключаться в высоком качестве молока (жирность, охлажден-ность), благодаря которому оно реализовано по более высоким ценам. Коэффициент регрессии при х2, как уже отмечено, экономически не обоснован.
Использование регрессионной модели для прогнозирования состоит в подстановке в уравнение регрессии ожидаемых значений факторных признаков для расчета точечного прогноза результативного признака или (и) его доверительного интервала с заданной вероятностью, как уже сказано в 9.6. Сформулированные там же ограничения прогнозирования по уравнению регрессии сохраняют свое значение и для многофакторных моделей. Кроме того, необходимо соблюдать системность между подставляемыми в модель значениями факторных признаков.
Формулы расчета средних ошибок оценки положения гиперплоскости регрессии в заданной многомерной точке и для индивидуальной величины результативного признака весьма сложны, требуют применения матричной алгебры и здесь не рассматриваются. Средняя ошибка оценки значения результативного признака, рассчитанная по программе ПЭВМ «Mi-crostat» и приведенная в табл. 9.7, равна 79,2 руб. на 1 га. Это лишь среднее квадратическое отклонение фактических значений дохода от расчетных по уравнению, не учитывающее ошибки положения самой гиперплоскости регрессии при экстраполяции значений факторных признаков. Поэтому ограничимся точечными прогнозами в нескольких вариантах (табл. 9.13).
Для сравнения прогнозов с базисным уровнем средних по совокупности значений признаков введена первая строка таблицы. Краткосрочный прогноз рассчитан на малые изменения факторов за короткое время и снижение трудообеспечен-ности.
386
Таблица 9.13 Прогнозы валового дохода по регрессионной модели
 Результат
неблагоприятен: доход снижается.
Долгосрочный прогноз А — «осторожный»,
он предполагает весьма умеренный
прогресс факторов и соответственно
небольшое увеличение дохода. Вариант
Б — «оптимистический», рассчитан на
существенное изменение факторов. Вариант
5 построен по способу, которым Агафья
Тихоновна в комедии Н. В. Гоголя «Женитьба»
мысленно конструирует портрет «идеального
жениха»: нос взять от одного претендента,
подбородок от другого, рост от третьего,
характер от четвертого; вот если бы
соединить все нравящиеся ей качества
в одном человеке, она бы не колеблясь
вышла замуж. Так и при прогнозировании
мы объединяем лучшие (с точки зрения
модели дохода) наблюдаемые значения
факторов: берем значение Х[ от хозяйства
№ 10, значение х2 от хозяйства № 2, значение
х3 от хозяйства № 16. Все эти значения
факторов уже существуют реально в
изучаемой совокупности, они не «ожидаемые»,
не «взятые с потолка». Это хорошо. Однако
могут ли эти значения факторов сочетаться
в одном предприятии, системны ли эти
значения? Решение данного вопроса
выходит за рамки статистики, оно требует
конкретных знаний об объекте
прогнозирования.
Результат
неблагоприятен: доход снижается.
Долгосрочный прогноз А — «осторожный»,
он предполагает весьма умеренный
прогресс факторов и соответственно
небольшое увеличение дохода. Вариант
Б — «оптимистический», рассчитан на
существенное изменение факторов. Вариант
5 построен по способу, которым Агафья
Тихоновна в комедии Н. В. Гоголя «Женитьба»
мысленно конструирует портрет «идеального
жениха»: нос взять от одного претендента,
подбородок от другого, рост от третьего,
характер от четвертого; вот если бы
соединить все нравящиеся ей качества
в одном человеке, она бы не колеблясь
вышла замуж. Так и при прогнозировании
мы объединяем лучшие (с точки зрения
модели дохода) наблюдаемые значения
факторов: берем значение Х[ от хозяйства
№ 10, значение х2 от хозяйства № 2, значение
х3 от хозяйства № 16. Все эти значения
факторов уже существуют реально в
изучаемой совокупности, они не «ожидаемые»,
не «взятые с потолка». Это хорошо. Однако
могут ли эти значения факторов сочетаться
в одном предприятии, системны ли эти
значения? Решение данного вопроса
выходит за рамки статистики, оно требует
конкретных знаний об объекте
прогнозирования.
Если, кроме количественных факторов, при многофакторном регрессионном анализе в уравнение включается и неколичественный, то применяют следующую методику: наличие неколичественного фактора у единиц совокупности обозначают единицей, его отсутствие — нулем, т.е. вводят так назы-
387

388

Число фиктивных переменных должно быть на единицу меньше числа градаций качественного (неколичественного) фактора. С помощью данного приема можно измерять влияние уровня образования, местожительства, типа жилища и других социальных или природных, неизмеряемых количественно факторов, изолируя их от влияния количественных факторов.
РЕЗЮМЕ
Связи, которые проявляются не в каждом отдельном случае, а лишь в совокупности данных, называются статистическими. Они выражаются в том, что при изменении значения фактора х изменяется и условное распределение результативного признака у: разным значениям одной переменной (фактора х) соответствуют разные распределения другой переменной (результата у).
Корреляционная связь — частный случай статистической связи, при котором разным значениям одной переменной х соответствуют разные средние значения переменной у.
Корреляционная связь предполагает, что изучаемые переменные имеют количественное выражение.
Статистическая связь — более широкое понятие, оно не включает ограничений на уровень измерения переменных. Переменные, связь между которыми изучается, могут быть как количественными, так и неколичественными.
Статистические связи отражают сопряженность в изменении признаков х и у, которая может быть вызвана не причинными отношениями, а так называемой ложной корреляцией. Например, в совместных изменениях х и у обнаруживается определенная закономерность, но она вызвана не влиянием
389
 390
390
 Математическое
описание корреляционной зависимости
результативной переменной от нескольких
факторных переменных называется
уравнением множественной регрессии.
Параметры уравнения регрессии оцениваются
методом наименьших квадратов (МНК).
Уравнение регрессии должно быть линейным
по параметрам.
Математическое
описание корреляционной зависимости
результативной переменной от нескольких
факторных переменных называется
уравнением множественной регрессии.
Параметры уравнения регрессии оцениваются
методом наименьших квадратов (МНК).
Уравнение регрессии должно быть линейным
по параметрам.
Если уравнение регрессии отражает нелинейность связи между переменными, то регрессия приводится к линейному виду (линеаризуется) путем замены переменных или их логарифмирования.
Вводя в уравнение регрессии фиктивные переменные, можно учесть влияние неколичественных переменных, изолируя их от влияния количественных факторов.
Если коэффициент детерминации близок к единице, то с помощью уравнения регрессии можно предсказать, каким будет значение зависимой переменной для того или иного ожидаемого значения одной или нескольких независимых переменных.
