60.Основные положения имитационного (статистического) моделирования

Метод статистического моделирования заключается в воспроизведении исследуемого процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Основан метод на многократном проведении испытаний построенной модели с последующей статистической обработкой полученных данных с целью определения характеристик рассматриваемого процесса в виде статистических оценок его параметров.Рассмотрим уравнение

(1) где y - параметр системы, требующий определения,

x – фазовая переменная, t – время,  – случайный параметр, закон распределения которого известен.

Если функция f существенно нелинейна, то для решения данной задачи нет универсальных методов решения (задача относится к классу NP), и достаточно полно отработанные регулярные методы поиска оптимальных решений можно применить только при использовании существенных упрощений, которые приведут к серьезной потери точности. Математическая модель станет неадекватной исследуемой системе, и моделирование будет только формой заблуждения.

Однако, как вы уже знаете из тематики методов построения алгоритмов, есть вероятностные методы решения такого рода задач. Если удается построить функцию и датчик случайных чисел с заданным законом распределения, то значение y может быть вычислено как

(2) где – значение i-й реализации.

Если является аналитической моделью процесса преобразования информации или технологического процесса обработки детали, то будет статистической моделью. Некоторые принципы и приемы построения статистических моделей будут рассмотрены позднее. Важно то, что при построении функции и датчика случайных чисел на бумаге, в подавляющем большинстве случаев достаточно легко реализовать их на ЭВМ в рамках соответствующего программного обеспечения. При этом результаты будут содержать ошибку, но эта ошибка меньше, нежели ошибки из-за допущений в аналитической модели. Кроме того, ошибка из-за применения статистической модели может быть количественно оценена. Этот прием распространяется и на более сложные случаи, когда в уравнение (1) входят не только случайные параметры, но и случайные функции.После получения на ЭВМ реализаций следует этап обработки статистики, позволяющий рассчитать, наряду с математическим ожиданием (2) и другие параметры , например дисперсию

.

В методе статистических испытаний для получения достаточно надежных результатов необходимо обеспечивать большое число реализаций , кроме того, с изменением хотя бы одного исходного параметра задачи необходимо производить серию из испытаний заново. При сложных моделях неоправданно большая величина может стать фактором, задерживающим получение результата. Поэтому важно правильно оценить необходимое число результатов. Доверительный интервал , доверительная вероятность , дисперсия D и число реализаций N связаны соотношением

(3), где – функция, обратная функции Лапласа.На практике можно воспользоваться соотношением

для принимая, с целью надежности, наибольшее значение из соотношения (3). Оценка дисперсии D может быть получена предварительно с помощью той же статистической модели при числе реализаций n, n<<N.

При построении статистических моделей информационных систем используется общий и прикладной математический аппарат. В качестве примера можно привести аппарат систем массового обслуживания.

61. Понятие и структура системы массового обслуживания.

В теории массового обслуживания изучаются системы, на вход которых поступает случайный поток заявок (требований), приходящихся в общем случае на случайные моменты времени. Поступившая заявка обслуживается в системе путем предоставления ей некоторых ресурсов на какое-то время и, будучи в той или иной мере обслуженной, покидает систему. Наиболее характерный момент функционирования систем массового обслуживания – это наличие очередей, в которых заявки ждут момента освобождения ресурсов, занятых обслуживанием других заявок. В простейшем случае система массового обслуживания (СМО) определяется потоком заявок, длиной очереди и дисциплиной обслуживания (порядком выбора заявок из очереди), числом каналов (приборов) обслуживания, распределением длительности обслуживания. В более сложных случаях рассматривается надежность приборов обслуживания. 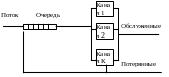Исследование СМО заключается в определении ее пропускной способности, времени ожидания заявки в очереди, загрузки каналов обслуживания. Структура многоканальной однофазной СМО приведена на рис. 5.1. Многоканальной называется такая СМО, где заявка может получить определенный тип обслуживания в одном из нескольких каналов. Многофазной называется СМО, характер обслуживания в которых является многоэтапным, например, переход заготовки от станка к станку, на совокупности которых реализуется технологический процесс изготовления детали. Поток заявок физически представляет собой явления одной природы, например, покупатели в магазине, посетители в парикмахерской, попытки позвонить по телефону, желания решить задачу с использованием компьютера и т. д. С математической точки зрения поток заявок на обслуживание характеризуется законом распределения случайной величины – времени между появлением соседних заявок.

Число мест в очереди – это число заявок, которые могут ожидать обслуживания, находясь в СМО. По ограничению очереди СМО разделяются на системы с нулевой длиной очереди, на системы с конечной (определенной) длиной очереди и системы с неограниченной длиной очереди. В системах с нулевой и конечной длиной очереди имеют место отказы – ситуации, когда в системе нет свободных каналов и все места в очереди уже заняты. Заявка, попавшая на отказ, считается потерянной.

Дисциплина очереди может быть без приоритетов или с приоритетами. И в том, и в другом случае выборка заявок на обслуживание может осуществляться по правилам: «первый пришел – первый вышел», «последний пришел – первый вышел», выбор заявки из очереди может быть организован случайным образом.

Время обслуживания заявки является случайной величиной. При анализе СМО определяется коэффициент загрузки канала – отношение времени, когда канал обслуживал заявки, к общему времени функционирования. В процессе работы каналы могут выходить из строя и восстанавливаться. В этом случае вводится понятие потока отказов и потока восстановлений, а также коэффициента готовности и коэффициента исправного действия. В общем случае заявка, во время обслуживания которой произошел отказ, считается потерянной.Успешно обслуженные заявки образуют поток обслуженных заявок. Заявки, не принятые на обслуживание по занятости всех каналов и мест в очереди, а также не обслуженные из-за выхода каналов из строя, образуют поток потерянных заявок. Сумма обслуженных и потерянных заявок равна числу заявок, поступивших на вход системы.

Таким образом, СМО характеризуется следующим набором параметров:

распределением длительности интервалов между заявками входящего потока р(а);числом мест в очереди;дисциплиной обслуживания заявок D;числом обслуживающих приборов (каналов) K;распределение длительности обслуживания заявок приборами p(b);

1. надежностью обслуживающих приборов.Указанный набор параметров полностью определяет порядок функционирования системы. Процесс функционирования количественно оценивается следующим набором основных характеристик:загрузкой, то есть средним по времени числом приборов (каналов), занятых обслуживанием;длиной очереди – средним числом заявок, ожидающих обслуживания;числом заявок, находящихся в системе (в очереди и на приборах);временем ожидания – средним временем пребывания заявок в очереди;временем пребывания заявки в системе;временем исправной работы приборов;количеством обслуженных и потерянных заявок.В многофазных СМО очереди могут быть на каждой фазе обслуживания. В тех случаях, когда возможно возвращение заявки после обслуживания на последующей фазе к обслуживанию на одной из предшествующих, говорят о более сложных образованьях - сетях массового обслуживания. Сеть массового обслуживания можно представить как совокупность узлов – отдельных СМО. Сеть массового обслуживания задается следующим набором параметров:параметрами источника заявок;структурой, определяющей конфигурацию связей и вероятности передачи заявок между узлами сети;параметрами СМО, образующими сеть.Функционирование сети массового обслуживания определяется совокупностью узловых и сетевых характеристик. Узловые характеристики оценивают работу каждой СМО и включают в себя весь набор их характеристик.

Задание структуры системы массового обслуживания

Структуру СМО можно описать следующими блоками

Для создания транзактов, входящих в модель, служит блок

GENERATE (генерировать), имеющий следующий формат: имя GENERATEA,B,C,D,E .В поле A задается среднее значение интервала времени между моментами поступления в модель двух последовательных транзактов. Если этот интервал постоянен, то поле B не используется. Если же интервал поступления является случайной величиной, то в поле B указывается модификатор среднего значения.В поле C задается момент поступления в модель первого транзакт. Поле D задает общее число транзактов, которое должно быть создано блоком GENERATE. Если это поле пусто, то блок генерирует неограниченное число транзактов до завершения моделирования.В поле E задается приоритет, присваиваемый генерируемым транзактам. Для присваивания параметрам начальных значений или изменения этих значений служит блок ASSIGN (присваивать), имеющий следущий

формат:имя  ASSIGN A,B,C .В поле A указывается номер или имя параметра, в который заносится значение операнда B. Если в поле A после имени (номера) параметра стоит знак + или -, то значение операнда B добавляется или вычитается из текущего содержимого параметра. В поле С может быть указано имя или номер функции-модификатора.Например, блок ASSIGN 5,0 записывает в параметр с номером 5 значение0.Для записи текущего модельного времени в заданный параметр транзакта служит блок MARK (отметить), имеющий следующий формат: имя  MARK A.В поле A указывается номер или имя параметра транзакта, в который заносится текущее модельное время при входе этого транзакта в блок MARK. Для изменения приоритета транзакта служит блок PRIORITY (приоритет), имеющий следующий формат: имя PRIORITY A,B.В поле A записывается новый приоритет транзакта. В поле B может содержаться ключевое слово BU, при наличии которого транзакт,вошедший в блок, помещается в списке текущих событий после всех остальных транзактов новой приоритетной группы. Для удаления транзактов из модели служит блок TERMINATE (завершить), имеющий следующий формат:имя  TERMINATE A ,Значение поля A указывает, на сколько единиц уменьшается содержимое так называемого счетчика завершений при входе транзакта в данный блок TERMINATE.Начальное значение счетчика завершений устанавливается управляющим оператором START (начать), предназначенным для запуска прогона модели. Поле A этого оператора содержит начальное значение счетчика. Например, простейший сегмент модели, состоящий всего из двух блоков GENERATE и TERMINATE и приведенный на рис. 1, в совокупности

с управлящим оператором START моделирует процесс создания случайного потока транзактов, поступащих в модель со средним интервалом в 100 единиц модельного времени, и уничтожения этих транзактов. Начальное значение счетчика завершений равно 1000. Каждый транзакт,проходящий через блок TERMINATE, вычитает из счетчика единицу, и таким образом моделирование завершится, когда тысячный по счету транзакт войдет в блок TERMINATE. При этом точное значение таймера в момент завершения прогона непредсказуемо. Следовательно, в приведенном примере продолжительность прогона устанавливается не по модельному времени, а по количеству транзактов, прошедших через модель.

GENERATE 100,40

TERMINATE 1

START 1000

В моделях систем массового обслуживания заявки обслуживаются приборами (каналами) СМО в течение некоторого промежутка времени прежде, чем покинуть СМО. Для задержки транзактов на определенный отрезок модельного времени, служит блок ADVANCE (задержать), имеющий следующий формат:имя  ADVANCE A,B

Операнды в полях A и B имеют тот же смысл, что и блока GENERATE. Следует отметить, что транзакты,входящие в блок ADVANCE, переводятся из списка текущих событий в список будущих событий, а по истечении вычисленного времени задержки возвращаются назад, в список текущих событий, и их продвижение по блок-схеме продолжается. Если вычисленное время задержки равно 0, то транзакт в тот же момент модельного времени переходит в следующий блок, оставаясь в списке текущих событий.