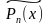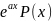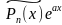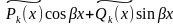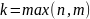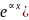- •2.Задачы, якия прыводзяцца да дыферэнцыяльных раунанняу.
- •3.Здр першага парадку: формы запису, рашэнни и интэгралы, геаметрычная интерпрытацыя частковага и агульнага рашэнняу.
- •4.Задача Кашы. Пункты иснавання и адзинасци рашэння. Умовы иснавання и адзинасци.
- •5.Агульныя, частковыя и асаблівыя рашэнні.
- •6.Метад изаклин для здр першага парадку
- •7.Др у поуных дыферэнцыялах. Прыкмета раунання у поуных дыферэнцыялах. Прыклады.
- •8.Др у поуных дыферэнцыялах. Интэгроуны множник. Прыклады
- •9.Др са зменными якия падзяляюцца, якия падзелены, раунанни якия да их прыводзяцца.
- •10.Аднародныя др (адносна зменных). Аднародныя функцыи
- •11. Др якия зводяцца да аднародных (адносна зменных)
- •12. Ладр першага парадку. Агульнае рашэнне
- •13. Ладр першага парадку. Структура агульнага рашэння. Метад Бернули
- •14. Рашэнне лндр першага парадку. Метад Лагранджа. Раунанне Бернули.
- •15.Тэарэма Пикара для здр першага парадку
- •16. Выкарыстанне прынцыпу сцискальных адлюстраванняу для доказу тэарэмы Пикара
- •18. Др якия дапускаюць панижэнне парадку.
- •§19. Лндр з пастаяннымі каэфіцыентамі.
- •20. Прастора рашэнняў ладр n-га парадку. Лінейная залежнасць і незалежнасць сістэмы функцый. Неабходная ўмова лінейнай залежнасці. Вранскіян. Дастатковая ўмова лінейнай незалежнасці. Прыклады.
- •22.Формула Астраградскага-Лиувиля
- •23. Дапаможныя звесткі
- •24.Ладр n-нага парадку з пастаянными каэфіцентамі. Характэрыстычнае раўнанне. Выпадкі розных сапраўдных каранёў і кратнага сапраўднага корня.
- •1 Выпадак
- •3 Выпадак
- •25. Ладр n-нага парадку з пастаянными каэфицентами. Характэрыстычнае раунанне. Выпадак каплекснага кораня.
- •2 Выпадак.
- •26. Ладр n-нага парадку з пастаянными каэфицентами и спецыяльнай правай часткай. Спецыяльная правая частка са здабыткам мнагаскладу и экспаненты.
- •27. Ладр n-нага парадку з пастаянными каэфицентами и спецыяльнай правай часткай. Спецыяльная правая частка са здабыткам экспаненты и синусам-косинусам.
- •28.Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вольныя ваганни у асяродзи без супрациулення.
- •29. Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вольныя ваганни у асяродзи з супрациуленнем.
- •30. Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вымушаныя ваганни у асяродзи без супрациулення.
- •31. Увядзенне элементарных функцый з дапамогай др. Экспанента
- •3.2 Экспоненциальная функция из r в r
- •32. Увядзенне элементарных функцый з дапамогай др. Трыганам.
- •3.1 Тригонометрические функции из r в r
- •33. Систэмы др. Астноуныя паняцци. Задача Кашы. Иснаванне и адзинасць рашэння. Агульныя и частковыя рашэнни.
- •34. Прывядзенне нармальнай систэмы да др н-нага парадку и наадварот.
- •35. Линейныя систэмы др. Лас и лнс. Линейная незалежнасць систэмы функцыянальных вектарау. Фундаментальная систэма. Вронскиян.
- •36. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Характэр. Раунанне. Паняцце аб метадзе Эйлера.
- •37. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак розных сапраудных каранёу.
- •38. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак розных каранёу сярод яких ёсць камплексныя.
- •39. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак, кали сярод каранёу сустракаюцца кратныя.
18. Др якия дапускаюць панижэнне парадку.
1. Раўнанні, якія ўтрымліваюць тольку незалежную зменную і вытворныя n-га парадку.
Раўнанне y(n)=f(x) інтэгруецца n-кратным паслядоўным яго інтэграваннем.
Прыклад:
y///=
y//=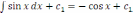
y/=
y=
2. Раўнанні, якія не ўтрымліваюць шукаемую функцыю.
F(x,y/,y//)=0 (1)
Парадак раўнання можа быць зніжаны на 1 з дапамогай падстаноўкі:
z(x)=y/
z/(x)=y//
(1): F(x,z,z/)=0
З дапамогай гэтай падстаноўкі z(x)=y(x) можна таксама панізіць парадак на k-раўнанняў выгляду:
F(x,y(k),y(k-1),…,y(k))=0
Прыклад: y//(x2+1)=2xy/
z(x)=y/
z/(x)=y//
z/(x2+1)=2xz

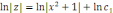 ,c1>0
,c1>0
z=c1(x2+1)
c1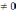
z=0
z=c1(x2+1),
c1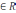
y/=c1(x2+1)
y=c1(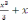 )+c2
c1,
c2
)+c2
c1,
c2
3.
Раўнанні якія не утрымліваюць незалежную
зменную
 ,
парадак гэтага р-ня можна знізіць на
1-ку з дапамогай падстаноўкі y
/=z(y);
,
парадак гэтага р-ня можна знізіць на
1-ку з дапамогай падстаноўкі y
/=z(y);

y(3)=…; y(4)=…; F(y, z, z/z,…,…)=0
Прыклад:
yy//-(y/)2=0;
y
/=z(y);
y//=zz/;
yzz/-z2=0;
 (z=0)
(z=0)
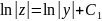 ;
z=C1y;
y/=C1y
=> y=C2eC1*x
;
C1,C2
R.
;
z=C1y;
y/=C1y
=> y=C2eC1*x
;
C1,C2
R.
§19. Лндр з пастаяннымі каэфіцыентамі.
Разгледзем раўнанне наступнага выгляду (1) L[y]=y(n) + a1 y(n-1) + … + an y = f(x), дзе f(x) – непарыўная на інтэтвале (a,b) ф-цыя. Будзем лічыць што мы ведаем ФСР адпаведнага аднароднага раўнаня, агульнае рашэнне (1), можна знайсці метадам Лагранджа.
У асобных выпадках, калі правая частка мае спецыяльны выгляд, агульнае рашэнне можна знайсці, як сумму агульнага рашэння ЛАДР + частковае рашэнне раўнання (1), якое знаходзіцца метадам нявызначанных каэфіцыентаў.
Агульныя выпадкі можна запісать ў выглядзе табліцы.
№ |
Правая частка |
Карані хар-га р-ня |
Выгл. частков. раш-я |
1 |
P(x) |
0 – не з’яўляецца каранем характарыстыўнага раўняння |
|
0 – з’яўляецца каранем характарыстыўнага раўняння кратнасці s |
|
||
2 |
|
a – не з’яўляецца каранем характарыстыўнага раўняння |
|
a – з’яўляецца каранем характарыстыўнага раўняння кратнасці s |
|
||
3 |
|
±β – не з’яўляецца каранем характарыстыўнага раўняння |
|
±β– з’яўляецца каранем характарыстыўнага раўняння кратнасці s |
|
||
4 |
|
α±β– не з’яўляецца каранем характарыстыўнага раўняння |
|
Лік α±β – з’яўляецца каранем характарыстыўнага раўняння кратнасці s |
|
Дзе
P(x),Q(x)
– мнагасклады ступені n,m
адпаведна, а
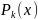 ,
,
 - мнагачлены ступені k
з нявызначанымі каэфіцыентамі.
- мнагачлены ступені k
з нявызначанымі каэфіцыентамі.
Разгледзм
падрабязна выпадак калі раўнанне мае
парадак 2,
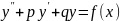 .
.
1)
Няхай
f(x)мае
выгляд
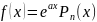 ,
дзе
,
дзе
 .
.
Бедзем шукаць частковае рашэнне ў выглядзе
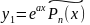 ,
дзе
,
дзе
 ,
дзе
,
дзе
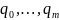 - невядомыя
лікі.
- невядомыя
лікі.
 ,
,
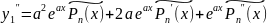
Падставім ў раўнанне (2)
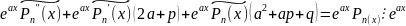
(3)
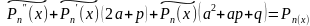
a) лік а не з’яўляецца каранем характарыстычнага раўнання г.зн. a2 +pa + q ≠ 0, тады з (3) можна вызначыць каэфіцыенты q0 , q1 ,…,qm прыраўноўваючы кафіцыенты пры аднолькавых ступенях х, злева і зправа.
Зправа стаіць мнагачлен з вядомымі каэфіцыентамі, а злева, мнагачлен каэфіцыенты якога нвдв знайсці.
б)
Няхай а аднакратны корань характарыстычнага
раўнання, тады відавочна ў (3) каэфіцыент
пры
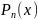 знікне і злева будзе стаяць мнагачлен
ступені n-1
, а справа ступені n,
пагэтаму частковае рашэнне трэба шукаць
ў выглядзе
знікне і злева будзе стаяць мнагачлен
ступені n-1
, а справа ступені n,
пагэтаму частковае рашэнне трэба шукаць
ў выглядзе
 ,
падстаўляючы гэты выраз ў (2) можна
таксама вызначыць каэ-ты
.
,
падстаўляючы гэты выраз ў (2) можна
таксама вызначыць каэ-ты
.
в) а корань кратнасці 2, у гэтым выпадку a2 + pa + q = 0 , частковае рашэнне шукаецца ў выглядзе

2)
Калі правая частка раўнання мае вызляд
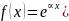 ,
у гэтым выпадку трэба выкарыстоўваць
формулы Эйлера
,
у гэтым выпадку трэба выкарыстоўваць
формулы Эйлера
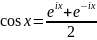 ,
,
 ,тады
,тады
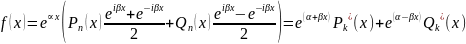
Дзе
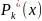 ,
,
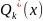 Мнагачлены
ступені k
з камплекснымі каэфіцыентамі, k=max{n,m}
Мнагачлены
ступені k
з камплекснымі каэфіцыентамі, k=max{n,m}
Згодна
з тэарэмай накладання (§16 т.2) частковае
рашэнне будзем шукаць у вызлядзе,
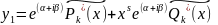 ,
дзе
,
-
мнагачлены з нявызначанымі каэфіцыентамі.
Далей, пасля знаходжання каэфіцыентаў,
застаецца зноў вярнуцца па формуле
Эйлера да сапраўднага выгляду.
,
дзе
,
-
мнагачлены з нявызначанымі каэфіцыентамі.
Далей, пасля знаходжання каэфіцыентаў,
застаецца зноў вярнуцца па формуле
Эйлера да сапраўднага выгляду.