
- •2.Задачы, якия прыводзяцца да дыферэнцыяльных раунанняу.
- •3.Здр першага парадку: формы запису, рашэнни и интэгралы, геаметрычная интерпрытацыя частковага и агульнага рашэнняу.
- •4.Задача Кашы. Пункты иснавання и адзинасци рашэння. Умовы иснавання и адзинасци.
- •5.Агульныя, частковыя и асаблівыя рашэнні.
- •6.Метад изаклин для здр першага парадку
- •7.Др у поуных дыферэнцыялах. Прыкмета раунання у поуных дыферэнцыялах. Прыклады.
- •8.Др у поуных дыферэнцыялах. Интэгроуны множник. Прыклады
- •9.Др са зменными якия падзяляюцца, якия падзелены, раунанни якия да их прыводзяцца.
- •10.Аднародныя др (адносна зменных). Аднародныя функцыи
- •11. Др якия зводяцца да аднародных (адносна зменных)
- •12. Ладр першага парадку. Агульнае рашэнне
- •13. Ладр першага парадку. Структура агульнага рашэння. Метад Бернули
- •14. Рашэнне лндр першага парадку. Метад Лагранджа. Раунанне Бернули.
- •15.Тэарэма Пикара для здр першага парадку
- •16. Выкарыстанне прынцыпу сцискальных адлюстраванняу для доказу тэарэмы Пикара
- •18. Др якия дапускаюць панижэнне парадку.
- •§19. Лндр з пастаяннымі каэфіцыентамі.
- •20. Прастора рашэнняў ладр n-га парадку. Лінейная залежнасць і незалежнасць сістэмы функцый. Неабходная ўмова лінейнай залежнасці. Вранскіян. Дастатковая ўмова лінейнай незалежнасці. Прыклады.
- •22.Формула Астраградскага-Лиувиля
- •23. Дапаможныя звесткі
- •24.Ладр n-нага парадку з пастаянными каэфіцентамі. Характэрыстычнае раўнанне. Выпадкі розных сапраўдных каранёў і кратнага сапраўднага корня.
- •1 Выпадак
- •3 Выпадак
- •25. Ладр n-нага парадку з пастаянными каэфицентами. Характэрыстычнае раунанне. Выпадак каплекснага кораня.
- •2 Выпадак.
- •26. Ладр n-нага парадку з пастаянными каэфицентами и спецыяльнай правай часткай. Спецыяльная правая частка са здабыткам мнагаскладу и экспаненты.
- •27. Ладр n-нага парадку з пастаянными каэфицентами и спецыяльнай правай часткай. Спецыяльная правая частка са здабыткам экспаненты и синусам-косинусам.
- •28.Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вольныя ваганни у асяродзи без супрациулення.
- •29. Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вольныя ваганни у асяродзи з супрациуленнем.
- •30. Прыкладанни др у физицы. Задача аб вольных и вымушаных ваганнях. Вымушаныя ваганни у асяродзи без супрациулення.
- •31. Увядзенне элементарных функцый з дапамогай др. Экспанента
- •3.2 Экспоненциальная функция из r в r
- •32. Увядзенне элементарных функцый з дапамогай др. Трыганам.
- •3.1 Тригонометрические функции из r в r
- •33. Систэмы др. Астноуныя паняцци. Задача Кашы. Иснаванне и адзинасць рашэння. Агульныя и частковыя рашэнни.
- •34. Прывядзенне нармальнай систэмы да др н-нага парадку и наадварот.
- •35. Линейныя систэмы др. Лас и лнс. Линейная незалежнасць систэмы функцыянальных вектарау. Фундаментальная систэма. Вронскиян.
- •36. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Характэр. Раунанне. Паняцце аб метадзе Эйлера.
- •37. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак розных сапраудных каранёу.
- •38. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак розных каранёу сярод яких ёсць камплексныя.
- •39. Интэграванне линейных систэм др з пастаянными каэфицэнтами. Метад Эйлера. Выпадак, кали сярод каранёу сустракаюцца кратныя.
14. Рашэнне лндр першага парадку. Метад Лагранджа. Раунанне Бернули.
Метад Лагранжа (метад варыяцыі адвольнай канстанты)
На практыцы для рашэння ЛНДР (1) карыстаюцца мадыфікацыяй метада Бернулі, якая носіць назву метада Лагранжа.
Будзем знаходзиць частковае рашэнне лндр (1).
Сутнасць метада знаходжання частковага рашэння заключаецца у тым, што спачатку рашаецца адпаведнае аднароднае дыф. раун., а затым знаходзицца агульнае рашэнне лндр з дапамогай замены канстанты С на невядомую функцыю С(х).
y=C -- рашэнне адпаведнага ладр.
Шукаем рашэнне (1) у выглядзе:
y=C(х) (7).
Падстауляем (7) у (1):
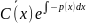 +
C(х)
(-p(x))+
C(х)
(p(x))=q(x)
+
C(х)
(-p(x))+
C(х)
(p(x))=q(x)
= q(x)
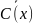 =
= =
q(x)*
=
q(x)*
C(х)= dx+С, C R.
Падставим гэта у (7) и атрымаем адказ.
Азн. Раунаннем Бярнули называецца раунанни наступнага выгляду:
y’+p(x)y=q(x)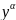 , дзе
, дзе
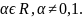
Памножым
абедзве частки на
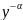 :
:
y’+ p(x)y = q(x)
z= -- прыменемгуту падстаноуку.
-- прыменемгуту падстаноуку.
z’=
(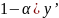
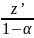 =
y’
=
y’
+ p(x) z= q(x).
Пасля
дамнажэння на
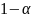 атрымаем лндр.
атрымаем лндр.
Прыклад 1:
ydx+xdy=0
d(xy)=ydx+xdy
d(xy)=0
xy=C
15.Тэарэма Пикара для здр першага парадку
Нахай дадзена ДР (1) з пачатковымі умовамі y(x0) = y0 (2). Калі функцыя f(x;y) здавальняе натупным умовам:
f(x;y)
– непарыўная па абедзьвух зменных x і
y ў замкненным абсягу D = {(x,y) | |x-x0|
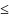 a, |y-y0|
b}, дзе a і b – дадзеныя дадатныя лікі.
Тады
M>0 | |f(x;y)|
M
a, |y-y0|
b}, дзе a і b – дадзеныя дадатныя лікі.
Тады
M>0 | |f(x;y)|
M
 пунктаў (x;y)
D
пунктаў (x;y)
D
Функцыя f(x;y) задавальняе ўмове Ліпшыца па другой зменнай, г.зн |f(x;y1)–f(x,y2)| L|y1–y2| пунктаў (x;y) D, дзе L 0 – пастаянная Ліпшыца
Тады
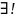 рашэнне у(х) ДР (1), якое задавальняе
пачатковай умове (2) і якое вызначана і
непарыўна дыферанцаванае
значэнняў x з абсягу |x-x0|
h, дзе
рашэнне у(х) ДР (1), якое задавальняе
пачатковай умове (2) і якое вызначана і
непарыўна дыферанцаванае
значэнняў x з абсягу |x-x0|
h, дзе
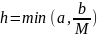 і якое
D для гэтых х.
і якое
D для гэтых х.
План доказу
Будуецца дапаможнае інтэгральнае раўнанне
Будуецца паслядоўнасць функцый, якая наз набліжанымі рашэннямі і высвятляюцца ўласцівасі набліжаных рашэнняў
Знаходзіцца ліміт паслядоўнасці набліжаных рашэнняў
Паказваецца, што ліміт паслядоўнасці з’яўляецца рашэннем зыходнай задачы Кашы
Паказваецца адзінасць знойдзенага рашэння
Доказ
1
Пакажам, што ДР (1) з пачатковымі ўмовамі (2) эквівалентна наступнаму інтэгральнаму раўнанню:
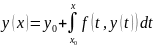 (3)
(3)
Пакажам,
што калі функцыя н(ч) задавальняе
інтэгральнаму раўнанню (3), то яна будзе
задавальняць задачы Кашы (1), (2). Т.як
функцыя f
непарыўная, то (3) можна дыферанцаваць
па х:
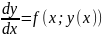 .
Падставім ў інтэгральнае раўнанне
пачатковую ўмову:
.
Падставім ў інтэгральнае раўнанне
пачатковую ўмову:
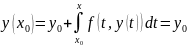 .
Пакажам, што з (1), (2) => (3). Праінтэгруем
ДР (1):
.
Пакажам, што з (1), (2) => (3). Праінтэгруем
ДР (1):
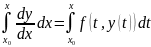 ;
;
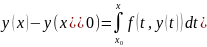 ;
;
2

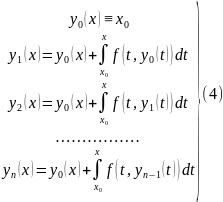
Высветлім уласцівасці:
Любая з ф-цый yk з’яўляецца непарыўнай, т.як y0(x) – пастаянная ф-цыя, y1 – непарыўная як ф-цыя непарыўнага верхняга ліміту
Для любога k ф-цыі yk(x) вызначаны ў абсягу |x-x0| h, а іх графік не выходзіць з D
|y1(x)-y0(x)|
=|y0(x)+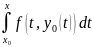 -y0(x)|
=|
|
|
-y0(x)|
=|
|
|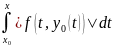 |
|
|
|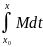 |=M|
|=M|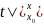 |=M|x-x0|
Mh
|=M|x-x0|
Mh
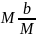 = b;
= b;
Па
ММІ: дапусцім, што пры |x-x0|
h не выходзіць з D, тады |yn(x)-y0(x)|
= |y0(x)+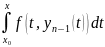 -y0(x)|
= =|
|
|
-y0(x)|
= =|
|
|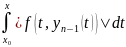 |
(па дапушчэнню ММІ і т.як рашэнне yn-1
не
выходзіць з D, то)
|
|=M|
|=M|x-x0|
Mh. Згодна з ММІ кожная yn
пры
|x-x0|
h, yn(x)
поўнасцю
належыць D.
|
(па дапушчэнню ММІ і т.як рашэнне yn-1
не
выходзіць з D, то)
|
|=M|
|=M|x-x0|
Mh. Згодна з ММІ кожная yn
пры
|x-x0|
h, yn(x)
поўнасцю
належыць D.
(4) – паслядоўнасць набліжэння.
3
Разгледзім наступны шэраг: y0(x)+[y1(x)–y0(x)]+…+[yn(x)–yn-1(x)]+…+. (5)
Частковая сума Sn(x)=yn(x). Па гэтаму задача можа быць зведзена да разгляду пытання аб збежнасці шэрагу. Пакажам, што шэраг збягаецца раўнамерна x |x-x0| h.
Ацэнім кожны з членаў функцыянальнага шэрагу:
|y0(x)|=|y0|;
|y1(x)-y0(x)| M|x-x0|;
|y2(x)-y1(x)|
|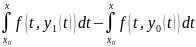 |
= |
|
= |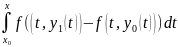 |
|
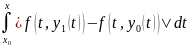 |
выкарст умову Ліпшыца:
|
|
выкарст умову Ліпшыца:
|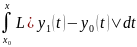 |
L
|
L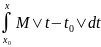 = LM
= LM = LM
= LM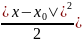 ;
;
………………………..
|yn-1(x)-yn-2(x)|
Ln-2
M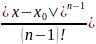 ;
;
|yn(x)-yn-1(x)|
|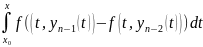 |
выкарст умову Ліпшыца і ул-ці інтэгралаў:
|
|
выкарст умову Ліпшыца і ул-ці інтэгралаў:
|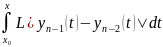 |
L = Ln-1
M
= Ln-1
M
|
L = Ln-1
M
= Ln-1
M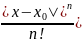 ;
;
Т.ч. атрымалі, што
|y0(x)|=|y0|;
|y1(x)-y0(x)| Mh;
|y2(x)-y1(x)|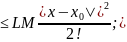
……………….
|yn(x)-yn-1(x)| Ln-1 M ;
Т.ч.
фунцыйны шэраг (5) абмежаваны зверху
лікавым шэрагам: y0
+ Mh +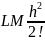 + Ln-1
M
+ Ln-1
M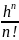 +… па прыкмеце Даламбера:
+… па прыкмеце Даламбера:
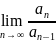 =
=
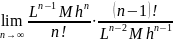 =
=
 = 0 < 1, т.ч. па прыкмеце Вейерштраса шэраг
(5) збягаецца раўнамерна пры адвольных
x
з прамежку |x-x0|
h. Кожна складнік шэрагу есць непарыўная
ф-цыя. Па гэтаму
= 0 < 1, т.ч. па прыкмеце Вейерштраса шэраг
(5) збягаецца раўнамерна пры адвольных
x
з прамежку |x-x0|
h. Кожна складнік шэрагу есць непарыўная
ф-цыя. Па гэтаму
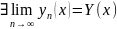 і Y(x)– непарыўная на абсягу |x-x0|
h ф-цыя і
і Y(x)– непарыўная на абсягу |x-x0|
h ф-цыя і
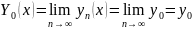
4
Пакажам,
што Y(x) – сапраўды рашэнне (3), г.зн.
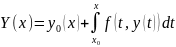 (6);
(6);
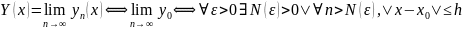 => |yn(x)-Y(x)|<
=> |yn(x)-Y(x)|<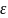 ;
;
|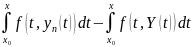 |
па ул-ці інтэгралаў і ўмове Ліпшыца
|
па ул-ці інтэгралаў і ўмове Ліпшыца
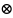
|yn(x)-y0(x)| b Пераходзячы да ліміту, атрымаем: |Y(x) – y0(x)| b
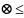
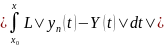 < L
|
< L
|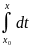 |
L
h;
|
L
h;
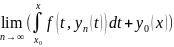 =
=
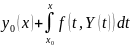 Г.зн
што y=Y(x) з’яўляецца рашэннем інтэгральнага
раўнання (3), якое вызначана і непарыўна
дыферанцаванае на прамежку |x-x0|
h (т.як згодна з (6) Y(x) – дыфер ф-цыя, т.як
у (6) зправа стаіць інтэграл со зменнай
верхняй мяжой ад непарыўнай ф-цыі).
Г.зн
што y=Y(x) з’яўляецца рашэннем інтэгральнага
раўнання (3), якое вызначана і непарыўна
дыферанцаванае на прамежку |x-x0|
h (т.як згодна з (6) Y(x) – дыфер ф-цыя, т.як
у (6) зправа стаіць інтэграл со зменнай
верхняй мяжой ад непарыўнай ф-цыі).
5
Няхай
на [x0;x0+ε]
(ε>0)
2 рашэнні: Y(x), Z(x), якія на гэтым [ ]не
супадаюць:Y(x)
Z(x),
г.зн што
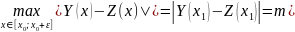 , x1
[x0;x0+ε].
, x1
[x0;x0+ε].
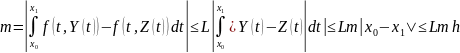 , т.ч
, т.ч
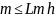 або 1
Lh
=>
або 1
Lh
=>
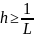 .
Але гэта не заўседы выконваецца ?!
.
Але гэта не заўседы выконваецца ?!

