8.Др у поуных дыферэнцыялах. Интэгроуны множник. Прыклады

Разгледзім ДР у дыферэнцыяльнай форме

M(x, y)dx + N(x, y)dy = 0 (1),

Лічым, што функцыі M(x, y), N(x, y) — непарыўныя па абедзюх зменных у некаторым адназвязным абсягу D плоскасці XOY, прычым

M²(x, y) + N²(x, y)  0.

Азначэнне 1: ЗДР (1) называецца раўнаннем у поўных дыферэнцыялах, калі яго левая частка з'яўляецца поўным дыферэнцыялам некаторай функцыі дзвюх зменных. Г.зн. ёсць ф-я . Так як du=0, то u(x;y)=C – агульны інтэграл раўнання (1).

Прыклад 1:

ydx+xdy=0

d(xy)=ydx+xdy

d(xy)=0

xy=C

Азначэнне 2: Часта бывае, што ДР (1) не з’яўл. ДР у поўных дыф-лах, але можна знайсці такую ф-ю 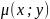, пры дамнажэнні абеіх частак (1) на гэтую ф-ю, ДР (1) становіцца раўнаннем у поўных дыф-х, тады называецца інтэгравальным множнікам.

Прыклад 1:

,

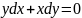
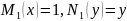Дамножым на

.

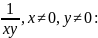
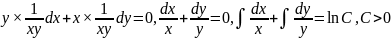
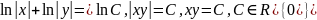
Прыклад 1:

ydx+xdy=0

d(xy)=ydx+xdy

d(xy)=0

xy=C

9.Др са зменными якия падзяляюцца, якия падзелены, раунанни якия да их прыводзяцца.

Разгледзім частковы выпадак ДР 1-га парадку выгляду:

(1)

Для гэтага раўнання выконваецца умова Эйлера: .

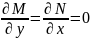Таму аг.інтэграл (1) мае выгляд: .

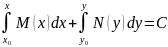(1) – ДР з пераменнымі, якія падзелены.

Разгледзім рашнанне: 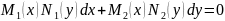(2).

Памножым (2) на , дзе .

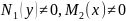Атрымалі: 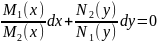. А гэта ДР з пераменнымі, якія падзелены.

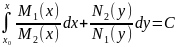- аг.інтэграл (2).

Заўважым, што рашэнні раўнанняў 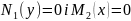могуць з’яўляцца асаблівымі рашэннямі. (2) – ДР з пераменнымі, якія падзяляюцца.

Прыклад 1:

,

Дамножым на

.

Заўвага: ДР са зменнымі, якія падзяляюцца, запісанае ў дыфер.форме, можна прывесці да раўнання выгляду , якое таксама наз.ДР з пераменнымі, якія падзяляюцца.

Разгледзім ДР выгляду пакажам, што гэта ДР можа быць зведзена да ДР з пераменнымі, якія падзяляюцца.

1)

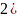
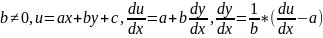
Прыклад 2:

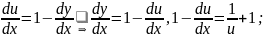
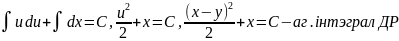
10.Аднародныя др (адносна зменных). Аднародныя функцыи

Азначэнне. Функцыя f(x,y) называецца аднароднай ступени m, кали для любога t з R мае месца наступная роунасць: f(tx, ty)= f(x,y).

Азначэнне. Дыф. раун. M(x,y)dx+N(x,y)dy=0 (1) называецца аднародным, кали функцыи M и N маюць адну и тую ж ступень аднароднасци.

Пакажам, што аднароднае ДР можа быць прыведзена да ДР з пераменными, якия падзяляюцца.

Няхай f(x,y) зъяуляецца аднароднай ступени m, тады: f(x,y)=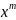 f(1, .

Сапрауды, т. я. f(x,y) аднародная ступени m, то 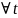выконваецца: f(tx, ty)= f(x,y).

Выберам 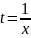. Падставим: f(1, )=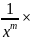 f(x,y), значыць f(x,y)= f(1, ).

Выкарыстаем гэту уласцивасць для дыф. раун. (1), т. я. M и N маюць ступень аднароднасци аднолькавую и роуную m, то:

M(1, dx+ N(1, )dy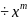=0 / ( =0 - ?)

M(1, )dx+N(1, )dy=0.

Выкарыстаем падстаноуку z= :

y=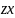 dy=zdx+xdz

M(1,z)dx+N(1,z)(zdx+xdz)=0

(M(1,z)dx+z*N(1,z))dx+x *N(1,z)dz=0 – дыф. раун. з пераменными, якия падзяляюцца.

Падзелим гэты выраз на: M(1,z)dx+z*N(1,z)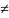 0.

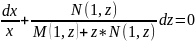
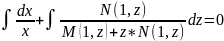
ln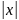 + 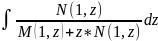=c – агульнае рашэнне дыф. раун. (1).

Кали z=a – корань раунання M(1,z)dx+z*N(1,z)=0, тады паупрамыя y=a*x могуць зъяуляцца або частковыми, або асабливыми рашэннями.

Асабливыми рашэннями таксама могуць быць паувоси x=0, кали y 0.

Заувага. Няхай дыф. раун. (1) аднароднае ступени m. Перапишым яго у выглядзе:

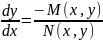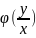, = = . Видавочна, што -- аднародная ступени 0, пагутаму дыф. раун. першага парадку вырашаннае адносна вышэйшай вытворнай будзе зъяуляцца аднародным, кали f(x,y) аднародная ступени 0. Гэта значыць:

– аднароднае, кали 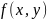аднародная ступени 0.