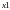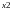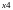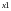Міністерство освіти і науки України Технічний коледж ну “Львівська політехніка” Курсова робота
З курсу
“Цифрова схемотехніка”
Виконав:
ст.гр 25-РТО
Жінчин А.С.
Перевірив:
Левандівський Б.В.
Львів 2009
Зміст
Завдання для курсової роботи 3
Методика проектування комбінаційних пристроїв 4
Етап 1 5
Етап 2 6
Математичний апарат цифрової мікросхемотехніки 8
Етап 3 10
Висновок 12
Використана література 13
2
Завдання для курсової роботи
Варіант №7
Таблиця №1
Логічні зміні |
Лог. Ф-я
|
||||
|
|
|
|
||
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
|
3
Методика проектування комбінаційних пристроїв
Проектування комбінаційного пристрою у загальному випадку складається з таких етапів:
Формалізованого подання алгоритму функціонування комбінаційного пристою у вигляді таблиці істинності.
Побудова електричної схеми комбінаційного пристрою згідно алгоритму одержаної логічної функції, побудованої на основі таблиці істинності.
Мінімізація одержаної логічної функції.
Подання мінімізованих логічних функцій у заданому логічному базисі (після мінімізації всі варіанти звести до базису І-НЕ)
Побудова електричної схеми комбінаційного пристрою згідно мінімізованої логічної функції.
На першому етапі здійснюється перехід від формалізованого подання комбінаційного пристою у вигляді таблиці істинності до алгоритму у вигляді логічної функції.
На другому етапі необхідно побудувати електричну схему, згідно одержаної логічної функції комбінаційного пристрою.
Третій етап полягає мінімізації логічної функції за допомогою аналітичного методу згідно математичного апарату цифрової мікросхемотехніки.
На четвертому етапі мінімізовану логічну функцію подають у заданому логічному базисі – в базисі І-НЕ.
П’ятий етап полягає у побудові електричної схеми комбінаційного пристрою згідно одержаної мінімізованої функції, приведеного до загального базису.
В процесі проектування конкретних комбінаційних цифрових пристроїв деякий з етапів може бути пропущений.
4
Етап 1
Усі логічні вирази в алгебрі логіці зустрічаються в двох формах представлення:
Представляє собою суму логічних змінних аргументів помножених між собою вона дістала назву диз’юнкції зміних множників. ЇЇ записують як універсально диз’юнктивна нормальна форма УДНФ .
Представляє собою логічне множення сум зміних аргументів вона дістала назву універсально коньюктивно нормальна форма УКНФ .
Якщо в нас функція представлена в УДНФ то її спів доданки одержали назву мінтерма.
Якщо в нас функція представлена в УКНФ то її співмножники одержали назву мактерма.
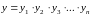
Оскільки
в таблиці істинності (таблиця 1) кількість
значень 0
і
1
логічної функції y
є однакове тому будемо будувати логічну
функцію за системою УДНФ. В таблиці
істинності (таблиця 1) є вісім логічних
одиниць логічної функції
,
тому мінтерм буде вісім.
5
Таблиця №2
Логічні зміні |
Логічна функція
|
|
|||||
|
|
|
|
||||
0 |
0 |
0 |
0 |
0 |
|
||
0 |
0 |
0 |
1 |
0 |
|
||
0 |
0 |
1 |
0 |
1 |
y1 |
||
0 |
0 |
1 |
1 |
0 |
|
||
0 |
1 |
0 |
0 |
1 |
y2 |
||
0 |
1 |
0 |
1 |
1 |
y3 |
||
0 |
1 |
1 |
0 |
1 |
y4 |
||
0 |
1 |
1 |
1 |
1 |
y5 |
||
1 |
0 |
0 |
0 |
1 |
y6 |
||
1 |
0 |
0 |
1 |
0 |
|
||
1 |
0 |
1 |
0 |
0 |
|
||
1 |
0 |
1 |
1 |
0 |
|
||
1 |
1 |
0 |
0 |
1 |
y7 |
||
1 |
1 |
0 |
1 |
0 |
|
||
1 |
1 |
1 |
0 |
1 |
y8 |
||
1 |
1 |
1 |
1 |
0 |
|
||
y
1=x1*x2*x3*x4;
y2=x1*x2*x3*x4;
y3=x1*x2*x3*x4;
y4=x1*x2*x3*x4;
y5=x1*x2*x3*x4;
y6=x1*x2*x3*x4;
y7=x1*x2*x3*x4;
y8=x1*x2*x3*x4.
y=y1+y2+y3+y4+y5+y6+y7+y8;
y = x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4+ +x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4.
О скільки у нас немає чотирьох входових елементів І перетворимо функцію так щоб використати чотирьох входові елементи І-НЕ для цього використаємо закон «подвійного заперечення»:
y = x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4+
+ x1*x2*x3*x4+ x1*x2*x3*x4+ x1*x2*x3*x4.
Етап 2
Функціональна електрична схема одержаної функції показана на рисунку 1.
6