
Задание № 4 Земля
Задача №1
Задана точность угловых измерений. Какой максимальной ошибке в километрах вдоль меридиана это соответствует?
Дано:
R⊗ = 6371 км
µ = 0” 9
Найти: m = ?
Решение:
3600 – 2R⊗π
0” 9 – x
![]()
Ответ: максимальная ошибка в километрах вдоль меридиана 0.028 км
Задача №2
Чему равна масса Земли, если угловая скорость Луны 13,2° в сутки, а среднее расстояние до нее – 384 400 км? Орбиту Луны считать круговой.
Дано:
ωл = 130 2
a = 3.844·105км
γ = 6.67·10-11км2/кг2
Найти: М⊗ = ?
Решение: В данном случае центробежная сила равна силе притяжения
![]()
![]()
![]() ω = 1302/24ч
= 1302/24·3600”
ω = 1302/24ч
= 1302/24·3600”
R=387400 км
D – увеличение расстояния до линии горизонта с повышением наблюдателя над поверхностью Земли
D=3.57√R D= 3.57 √387400= 2222.02 км
Учитывая это можно записать
![]() =>
=>![]()
![]()
Ответ: М⊗ = 6·1024кг
Задача №3
Определить период обращения искусственного спутника Земли, если наивысшая точка его орбиты над Землей 5000 + N км, а наинизшая – 300 + N км. Сравните движение спутника с обращением Луны (период обращения и среднее расстояние для Луны приведены в прил. 3).
Дано:
a1=5000 + N км
a2=300 + N км
R⊗= 6371 км
Найти: T = ? Tл/T = ?
Решение:
Большая полуось эллипса по которой движется спутник
![]()
Согласно третьему закону Кеплера
![]()
Период обращения спутника по круговой орбите
![]()
Период обращения по эллиптической орбите
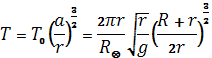
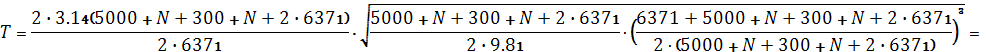 2
ч 32 мин =152 мин
2
ч 32 мин =152 мин
Луна обращается за 27 сут 24ч 60 мин = 38880 мин
![]()
Ответ: Период обращения искусственного спутника Земли = 152 мин.
Спутник вращается быстрее Земли в 256 раз
Задача №4
Определить длину дуги меридиана между пунктами А и В, если в пункте А полуденное Солнце находится в зените 21 марта и 23 сентября, а в пункте В – 22 июня, считая Землю шаром. R = 6 371 км.
Дано:
RΘ = 6 371 км
Найти: S = lAB = ?
Решение:
Длину дуги меридиана определяют из формулы
![]()
![]()
φ1 и φ2 широта местности φ1-φ2 = 1800 между днями равноденствия
![]()
Ответ: длина дуги меридиана между пунктами А и В = 20004.94 км
Задание № 5 Звезды. Галактика.
Задача №1
Используя значения видимой и абсолютной звездных величин для своего варианта 1 т.к. нет 90-го, определить расстояние до звезды в парсеках. Выразить это расстояние в световых годах и астрономических единицах. Найти параллакс звезды.
Дано:
Сириус
m = -1.5
M = 1.4
Найти: D, π =?
Решение:
Расстояние до звёзд измеряется в парсеках
1пк = 206265 а.е. =3.258 св.г = 3.086 ⋅ 1013км
Используем формулу:
![]()
![]()
D = 9.55 пк = 1969830.75 а.е. = 31.11 св.г. = 29.47 ⋅ 1013км
Параллакс найдем:
![]()
Ответ: Расстояние до Сириуса = 9.55 пк = 1969830.75 а.е. = 31.11 св.г. = 29.47 ⋅ 1013км
Параллакс звезды = 0.11”
Задача №2
Известны период обращения двойной звезды, большая полуось видимой орбиты и параллакс. Определить сумму масс и массы звезд в отдельности.
Дано:
T = 0.86 г
а =6”0
π = 0.076
m1/m2=1/8
Найти:
(m1+m2) =?
m1 =?
m2 =?
Решение:
Третий закон Кеплера, уточненный Ньютоном, позволяет определить массу визуально-двойной звезды, если известен ее параллакс.
![]()
![]()
![]()
8m1
=m2
9m1
= ![]() m1
= 72102.4
m1
= 72102.4![]()
m2 = 576819
Ответ: сумма масс двойной звезды ≈ 648922 массы Солнца и массы звезд в отдельности: m1 ≈ 72102.4 , m2 ≈ 576819
Задача №3
Определить расстояние до галактики и ее диаметр. Исходными данными являются: скорость удаления галактики и видимый угловой диаметр.
Дано:
V = 9000 км/с
Н = 50 км/(с⋅Мпк)
d” = 70”
Найти: r = ? d = ?
Решение:
По закону Хабба:

![]()
Ответ: расстояние до галактики = 180 Мпк и ее диаметр ≈ 0.061Мпк
