2.2 Оценивание параметров моделей с гетероскедастичностью возмущений

Рассмотрим использование обобщенного метода наименьших квадратов для корректировки гетероскедастичности возмущений.

Пусть строится линейная регрессионная модель (0). Будем считать, что модель гетероскедастична, т. е. дисперсии возмущений (i=1, 2, …, n) не равны между собой, а сами возмущения не коррелированны и их математические ожидания равны нулю. Это означает, что ковариационная матрица вектора возмущений  будет диагональной:

.

(0)

Для оценки параметров такой модели используется взвешенный метод наименьших квадратов (Weighted Least Squares), являющийся частным случаем обобщенного МНК.

Сущность взвешенного метода наименьших квадратов состоит в том, что каждый квадрат остатка (i=1, 2, …, n) «взвешивается» с помощью коэффициента , где (_i) — среднее квадратическое отклонение i-го возмущения. Тем самым добиваются равномерного вклада остатков в остаточную сумму квадратов, что приводит, в конечном счете к получению несмещенных и наиболее эффективных оценок параметров модели.

Условие взвешенного метода наименьших квадратов имеет вид:

.

(0)

Вектор b* оценок параметров модели определяется по формуле (0).

На практике, однако, средние квадратические отклонения возмущений (_i) почти никогда не бывают известны. Поэтому для применения взвешенного метода наименьших квадратов, необходимо сделать предположение о значениях (_i).

Весьма часто считают, что среднее квадратическое отклонение возмущений пропорционально значениям одного из факторов, предположительно делающих выборочную совокупность неоднородной.

Пусть имеются исходные данные для построения модели множественной регрессии (табл. 1).

Таблица	1
Исходные данные для построения модели множественной регрессии

Номер наблюдения (объекта)	Значение результата Y	Набор факторов и их значения
		X0	X1	X2	…	Xj	…	Xp
1	y1	1	x11	x12	…	x1j	…	x1p
2	y2	1	x21	x22	…	x2j	…	x2p
…	…	…	…	…	…	…	…	…
i	yi	1	xi1	xi2	…	xij	…	xip
…	…	…	…	…	…		…	…
n	yn	1	xn1	xn2	…	xnj	…	xnp

Представим модель (0) в развернутом виде:

(i=1, 2, …, n).

(0)

Если предположить, что среднее квадратическое отклонение возмущений (_i) (i=1, 2, …, n) пропорционально значениям x_ij фактора X_j (или, что одно и тоже — дисперсия возмущений пропорциональна квадрату значений фактора X_j), то исходные данные преобразуются их делением на соответствующие значения x_ij (i=1, 2, …, n). Такое преобразование называется масштабированием исходных данных по фактору X_j. (табл. 2).

Таблица	2
Масштабирование исходных данных по фактору Xj

Номер наблюдения (объекта)	Значение результата Y	Набор факторов и их значения
		X0	X1	X2	…	Xj	…	Xp
1	y1/x1j	1/x1j	x11/x1j	x12/x1j	…	1	…	x1p/x1j
2	y2/x2j	1/x2j	x21/x2j	x22/x2j	…	1	…	x2p/x2j
…	…	…	…	…	…	…	…	…
i	yi/xij	1/xij	xi1/xij	xi2/xij	…	1	…	xip/xij
…	…	…	…	…	…	…	…	…
n	yn/xnj	1/xnj	xn1/xnj	xn2/xnj	…	1	…	xnp/xnj

Таким же образом преобразуется и модель (0):

(i=1, 2, …, n),

(0)

или, что одно и тоже —

(i=1, 2, …, n),

(0)

Введем обозначения.

Пусть , , , , …, , , тогда преобразованная модель окончательно будет иметь вид:

(i=1, 2, …, n).

(0)

Параметры преобразованной модели (0) оцениваются обычным методом наименьших квадратов. Если предположение о пропорциональности среднего квадратического отклонения возмущений значениям фактора X_j имеет основание, то «новое» возмущение _i будет иметь постоянную и притом — наименьшую дисперсию, а коэффициенты уравнения регрессии окажутся несмещенными и эффективными оценками параметров модели (0). Вместе с тем следует иметь в виду, что новые преобразованные переменные получают другое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным. Поэтому численно оценки параметров моделей (0) и (0) в общем случае не совпадают.

Если строится линейная модель парной регрессии Y по X

(i=1, 2, …, n),

(0)

то она трансформируется в модель

(i=1, 2, …, n),

(0)

в которой свободный член и угловой коэффициент как бы поменялись местами.

На практике иногда имеет смысл попробовать использовать одновременно несколько факторов для масштабирования исходных данных.

Если каждый раз получаются сходные результаты и тесты Голдфельда–Квандта по всем факторам не выявляют гетероскедастичность возмущений, то эту проблему можно считать решенной.

В ряде случаев дисперсия возмущений зависит не от включенных в модель факторов, а от тех, которые не включены в модель, но играют существенную роль в исследуемой зависимости. Иногда для устранения гетероскедастичности необходимо изменить спецификацию модели, например, линейную на логарифмическую и т.д.
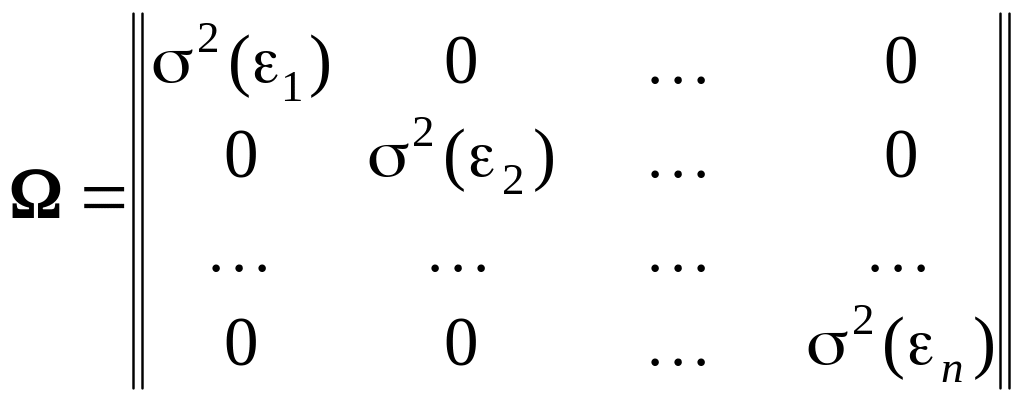