Контрольні питання

1. Які основні причини використання систем одночасних рівнянь?

2. У чому основна відмінність між структурними рівняннями системи і рівняннями у зведеній формі?

3. Чому звичайний МНК практично не використовується для оцінювання систем одночасних рівнянь?

4. У чому суть непрямого методу найменших квадратів (НМНК)?

5. Назвати необхідні і достатні умови ідентифікованості систем.

6. Які системи можна оцінювати 1МНК?

7. У чому полягає суть двокрокового методу найменших квадратів.

Лабораторна робота № 5 (4 години) Тема. Модель часових рядів: виділення тренду та сезонних коливань з використанням пакета Statistica

Мета роботи: побудова моделі часових рядів та прогноз досліджуваного показника на певний період.

Завдання 1

За наведеними вихідними даними відповідно до варіанта необхідно використовувати пакет Statistica:

1. За даними варіанта побудувати графік вихідних даних та зробити попередній висновок про наявність чи відсутність сезонних коливань.

2. Побудувати корелограму та зробити висновок про наявність чи відсутність сезонних коливань.

3. Побудувати адитивну та мультиплікативну модель часового ряду.

4. Побудувати графіки циклічної, трендової та випадкової компонент.

5. Побудувати графіки фактичних і теоретичних значень рівнів часового ряду для кожної моделі.

6. Порівняти отримані результати за кожною моделлю, оцінивши якість моделей за коефіцієнтом детермінації, та зробити висновки.

Вимоги до оформлення звіту

Звіт про проведення даної лабораторної роботи оформлюється в окремому зошиті згідно з встановленими вимогами до оформлення звітів і містить:

• назву, тему, завдання, опис мети лабораторної роботи;

• вихідні дані варіанта;

• рішення поставлених завдань з використанням пакета Statistica, що супроводжуються коментарями.

Зразок виконання лабораторної роботи

Існують дані про обсяг товарообігу приватного підприємства за певний проміжок часу. Вихідні дані введено в пакет Statistica 6.0 (рис. 5.1). 

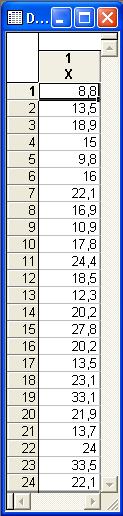
Рис. 5.1. Вхідний часовий ряд

Для того, щоб увійти в модуль Анализ временных рядов и прогнозирование потрібно обрати модуль Time series / Forecasting. Загальне призначення модуля – побудувати просту модель, що описує ряд, згладити його, спрогнозувати майбутні значення часового ряду на основі фактичних значень, побудувати регресійні залежності одного ряду від другого і т.д. Стартову панель модуля наведено на рис. 5.2.

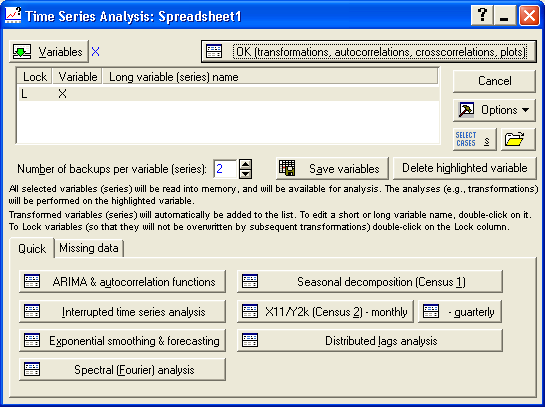
Рис. 5.2. Стартове вікно модуля Анализ временных рядов и прогнозирование

Зліва від імені обраної змінної стоїть значок L у графі Lock, який означає, що змінна закрита на ключ і не може бути видалена без переривання аналізу.

Щоб побудувати графік вихідних даних, у вікні необхідно натиснути кнопку ОК, в результаті чого з’явиться діалогове вікно (рис. 5.3).

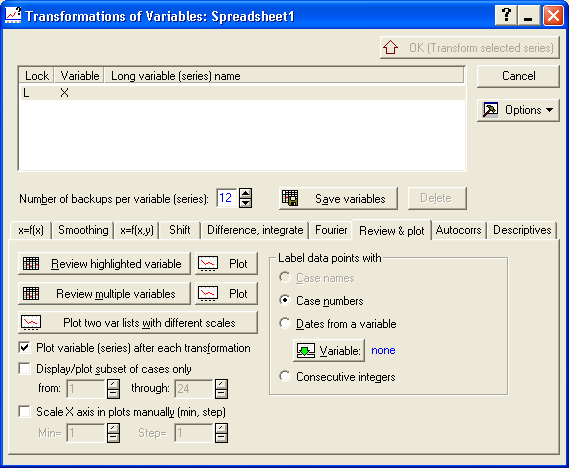
Рис. 5.3. Діалогове вікно

Необхідно звернути увагу на опцію Plot variables (series) after each transformation – Построить график переменных (ряда) после каждой трансформации в данном окне. Після встановлення система буде автоматично видавати графік перетворених даних після кожного перетворення ряду.

У нижній частині вікна необхідно перейти на вкладку Smoothing – Сглаживание та виділити опцію N-pts mov. averg. – Сглаживание по методу скользящих средних. Дана функція дозволяє провести згладжування по двох, трьох і більше точках. Після натиснення на ОК на екрані з’являється графік згладженого ряду. Для того, щоб переглянути одночасно вихідні дані і результати процедури простого ковзного середнього, необхідно перейти на вкладку Review&plot і натиснути кнопку Plot біля Review multiple variables (рис. 5.3). Отримаємо такий графік:

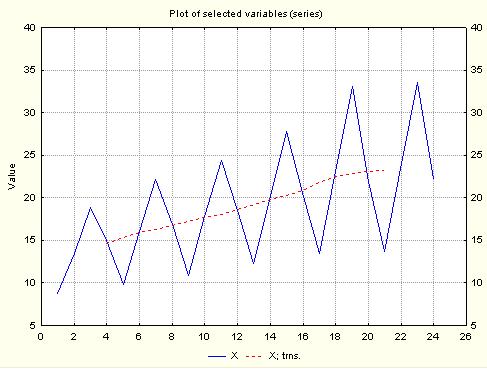
Рис. 5.4. Графік початкового ряду та згладженого за методом ковзних середніх

Щоб перевірити, чи має ряд сезонну складову, необхідно побудувати корелограму. Для цього необхідно перейти на вкладку Autocorrelations (Автокорреляция). У результаті отримаємо корелограму ряду (рис. 5.5).

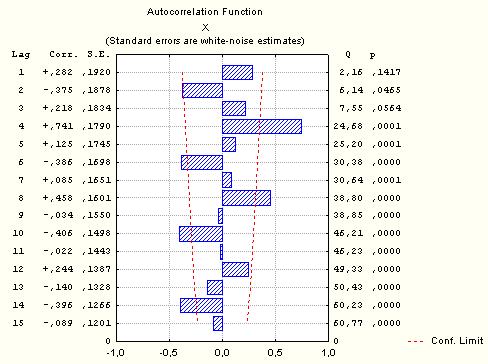
Рис. 5.5. Корелограма часового ряду

Корелограма показує, що ряд має сезонну компоненту з періодом, що дорівнює чотирьом.

Seasonal decomposition – Сезонная декомпозиция дозволяє виділити в ряді сезонну компоненту, що позначається як S, тренд-циклічну компоненту ТС і нерегулярну (випадкову) складову Е. Модель може бути мультиплікативною чи адитивною.

Натиснути кнопку Seasonal decoposition (Census 1) – Сезонная декомпозиция і відкрити діалог Сезонная декомпозиция (рис 5.6).

У центральній частині панелі знаходяться опції, що дозволяють задати модель ряду. Ці опції об’єднані в групу Seasonal model – Сезонная модель:

Additive – адитивна;

Multiplicative – мультиплікативна.

В опції Seasonal lag – Сезонный лаг задається число сезонних індексів.

Наступна група опцій дозволяє визначити такі складові:

Moving averages – ковзні середні;

Ratios/Differences – Отношения/Разности. Якщо модель мультиплікативна, береться відношення, якщо адитивна – різниця вихідного ряду і тренду;

Seasenal factors – сезонні індекси;

Seasonal adj. series – ряд без сезонної складової;

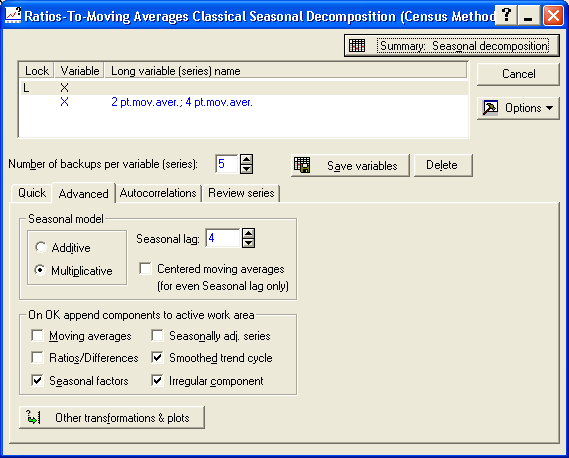
Рис. 5.6. Діалог (Сезонная декомпозиция)

Smoothed trend cycle – згладжена тренд-циклічна компонента;

Irregular components – нерегулярна (випадкова) складова.

Запустити процедуру сезонної декомпозиції, натиснувши на кнопку ОК (Perform seasonal decomposition) – Да (Выполнить сезонную декомпозицию). Результати розрахунків для мультиплікативної моделі виводяться у вигляді таблиці (рис. 5.7).

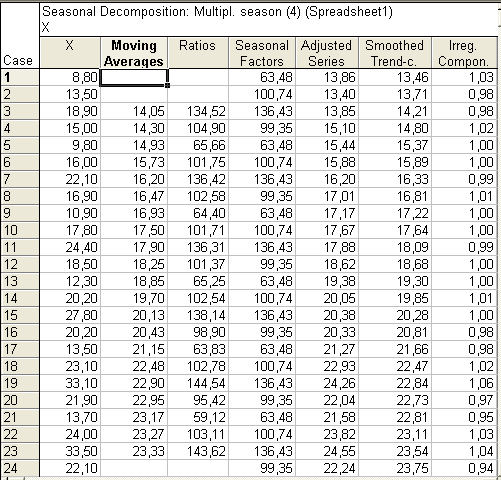
Рис. 5.7. Сезонна декомпозиція ряду для мультиплікативної моделі

У другому стовпці (Moving Averages) наведені прості ковзні середні по чотирьох точках часового ряду (без центрування), причому в таблиці значення ковзних середніх зміщені на ½ рядка: середнє арифметичне чотирьох перших точок 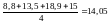визначається як значення ковзного середнього в третій точці і т.д.

У третьому і четвертому стовпцях (Rations і Seasonal Factors) розраховуються відповідно відношення елементів вихідного ряду до ковзного середнього (в процентах) і скореговані сезонні індекси.

У п’ятому стовпці (Adjusted Series) розраховується ряд, скоригований на сезонні індекси, тобто ряд без сезонної складової. Розраховується діленням вихідного ряду (Х) на сезонні індекси і множенням результату на 100.

У шостому стопці розраховується згладжена тренд-циклічна складова (Smoothed Trend-c.), тобто наводяться результати згладжування ряду, скорегованого на сезонні індекси.

Компоненти ряду відображаються на графіку. Для цього виділяється Seasonal Factors (Сезонні компоненти) в активній робочій області.

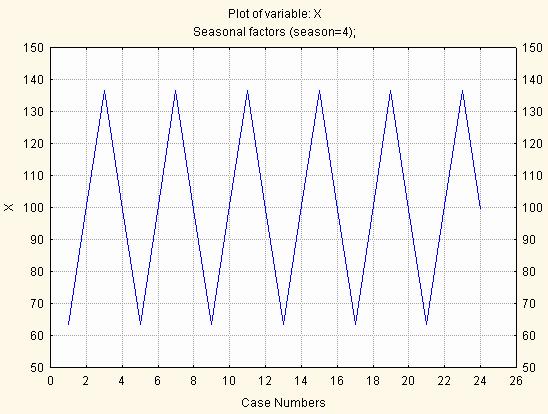
Рис. 5.8. Графік сезонної компоненти

Отже, стійкий рисунок сезонної мінливості притаманний даному ряду. За допомогою цієї сезонної складової можна скорегувати вхідний ряд, тобто вирахувати її із початкового ряду у випадку адитивної моделі і розділити значення початкового ряду на значення сезонної компоненти для мультиплікативної моделі (рис. 5.9).

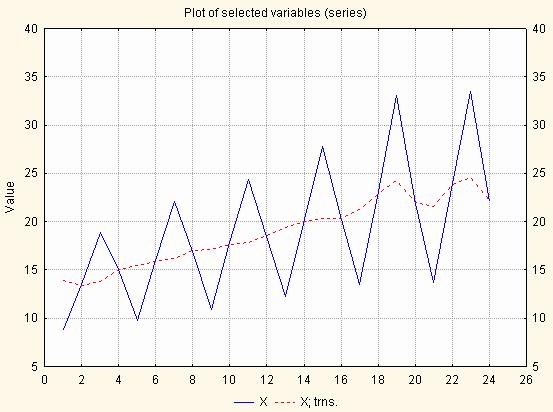
Рис. 5.9. Графік початкового ряду та ряду з сезонною поправкою

Скоригований ряд більше не містить сезонних коливань. Після цього можна згладити отриманий ряд для того, щоб прибрати випадкову складову. Результат згладжування ряду з сезонною поправкою є його тренд-циклічна компонента (ТС), тому що вона показує загальний тренд і цикли, що присутні в ряді. Циклічна компонента відрізняється від сезонної компоненти тим, що цикли, як правило, мають тривалість більше одного сезону і не мають постійного періоду. На наступному графіку побудована тренд-циклічна компонента і ряд з сезонною поправкою (рис. 5.10).

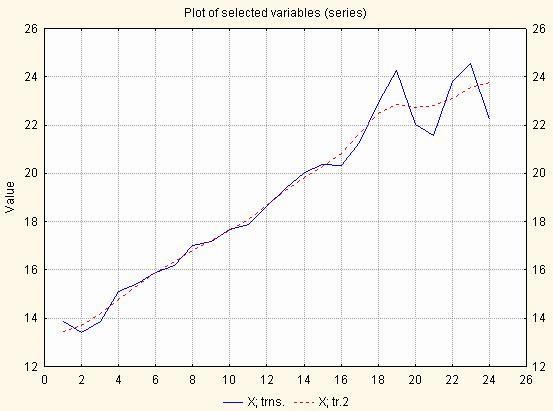
Рис. 5.10. Графік тренд-циклічної компоненти ряду і ряду з сезонною поправкою

Необхідно вибрати лінійну модель для побудови тренду та розрахувати оцінки параметрів рівняння регресії:

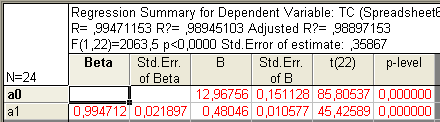
Рис. 5.11. Вікно оцінки параметрів моделі тренду

Параметри статистично значимі за критерієм Стьюдента. Модель можна подати так: 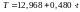. Значення трендової компоненти визначимо як теоретичні значення побудованої моделі, ініціювавши кнопку Residuals and Predicted.

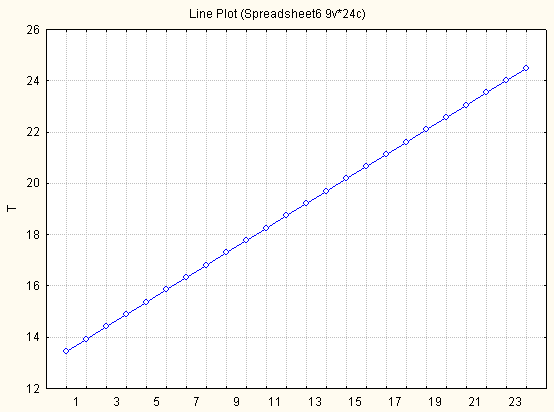
Рис. 5.12. Графік трендової компоненти часового ряду

Циклічна компонента розраховується як 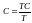і будується її графік (рис. 5.13).

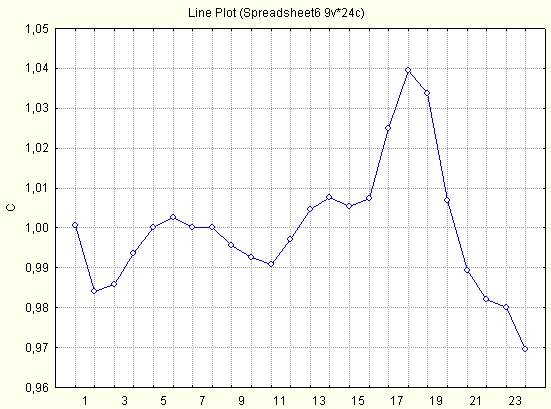
Рис. 5.13. Графік циклічної компоненти часового ряду

Необхідно розглянути також випадкову складову, що містить залишкові коливання ряду. Залишки можна розглянути одночасно з початковим рядом і рядом з сезонною поправкою.

Використовуючи процедуру График 2-х списков переменных в разных масштабах, проаналізуємо перший список змінних, якому відповідає ліва вісь Y, вихідний ряд і сезонне корегування ряду, а за другим списком – нерегулярну компоненту (рис. 5.14).

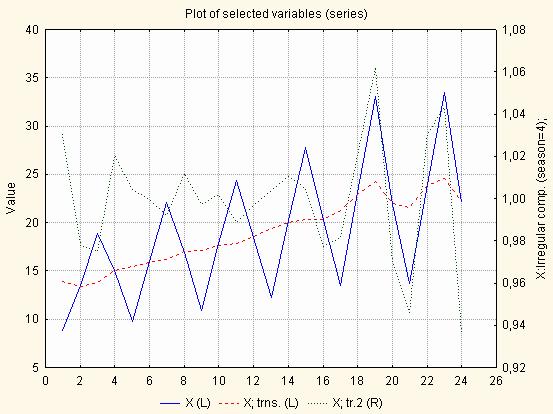
Рис. 5.14. Графік початкового ряду, ряду з сезонним корегуванням та випадкової компоненти

Теоретичні значення розраховуються як 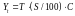. Потім будується графік теоретичних та емпіричних даних (рис. 5.15).

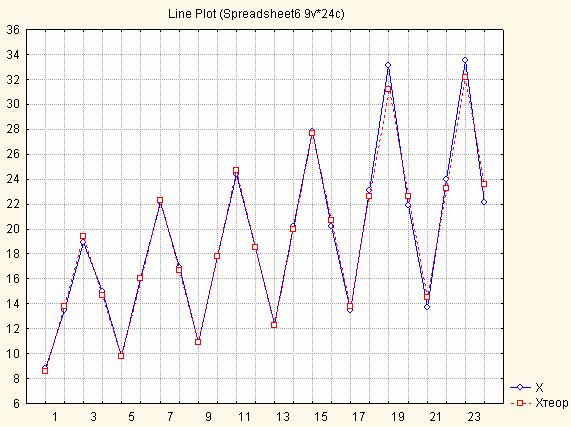
Рис. 5.15. Теоретичні та емпіричні значення ряду

Аналогічно проводиться адитивна декомпозиція часового ряду. Далі необхідно зробити висновок про якість побудованих моделей та визначити більш якісну з них.