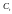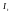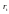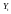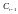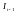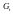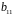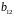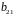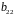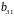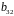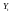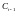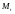Завдання 2

Оскільки отримані моделі в завданні 1 рівноцінні, то можна обрати будь-яку. Наприклад, модель, оцінки якої розраховані за методом Ейткена: .

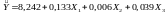Використовуючи циклічний коефіцієнт автокореляції, перевіримо наявність автокореляції залишків:

.

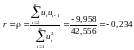Абсолютне значення коефіцієнта автокореляції порівнюється з табличним: 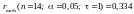. Оскільки 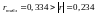, то автокореляція залишків відсутня.

Наявність автокореляції залишків перевіряється за допомогою критерію Дарбіна–Уотсона. Тест Дарбіна–Уотсона базується на простій ідеї: якщо кореляція похибок регресії не дорівнює нулю, то вона присутня в залишках регресії 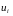, що отримуються в результаті застосування 1МНК. У тесті Дарбіна–Уотсона для оцінки кореляції використовується така статистика:

.

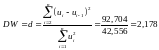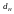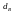Для даного критерію існує два порогових значення і , що залежать тільки від кількості спостережень, регресорів і рівня значимості.

Якщо фактично спостережуване значення d:

а) 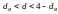 , то гіпотеза про відсутність автокореляції не відхиляється (приймається);

б) 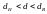 чи , то питання про прийняття гіпотези залишається відкритим (область невизначеності критерію);

в) 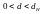 , то приймається альтернативна гіпотеза про позитивну автокореляцію;

г) 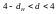 , то приймається альтернативна гіпотеза про негативну автокореляцію.

Критичні значення d-статистики (нижня ( ) та верхня ( ) межа) можна знайти в статистичних таблицях для рівнів значимості 0,01; 0,025; 0,05. Для даного випадку = 0,774, а  = 1,774. Тобто можна зробити висновок про те, що автокореляція залишків відсутня.

Контрольні питання

1. Яке явище називається гетероскедастичністю?

49. У чому суть гетероскедастичності?

50. До яких наслідків призводить порушення припущення про гомоскедастичність?

51. Назвати методи визначення гетероскедастичності.

52. За яких умов застосовується параметричний тест Гольдфельда–Квандта?

53. На чому базується тест Глейсера?

54. Що означає автокореляція залишків? До яких наслідків вона при­зводить?

55. Які причини виникнення автокореляції?

56. Чим відрізняється УМНК при автокореляції?

57. Як впливає автокореляція на оцінку параметрів моделі?

58. Навести тести наявності автокореляції залишків.

59. Стисло охарактеризувати алгоритм методу Дарбіна–Уотсона.

60. Зобразити графічно зони автокореляційного зв’язку за критерієм Дарбіна–Уотсона.

61. Охарактеризувати алгоритм застосування критерію фон Неймана.

62. Н а основі яких методів можна оцінити параметри моделі з автокорельованими залишками?

ЛАБОРАТОРНА РОБОТА № 4 (2 години)

Тема. Економетричні моделі на основі системи структурних рівнянь

Мета роботи: набуття навичок проведення ідентифікації рівнянь системи структурних рівнянь.

Завдання 1

Дано систему економетричних рівнянь (додаток В). Необхідно:

1. Виділити ендогенні та екзогенні змінні системи.

63. Застосувати необхідну і достатню умову ідентифікації, визначити, чи ідентифіковане кожне з рівнянь системи.

64. Визначити метод оцінки параметрів моделі.

Вимоги до оформлення звіту

Звіт про проведення даної лабораторної роботи оформлюється в окремому зошиті згідно з встановленими вимогами до оформлення звітів і містить:

• назву, тему, завдання, опис мети лабораторної роботи;

• вихідні дані варіанта;

• рішення поставлених завдань, що супроводжуються коментарями.

Зразок виконання лабораторної роботи

Вивчається така модель:

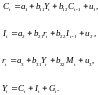
де C – витрати на споживання в період t;

Y – ВВП в період t;

I – інвестиції в період t;

r – процентна ставка в період t;

M – грошова маса в період t;

G – державні витрати в період t;

C_t-1 – витрати на споживання в період t–1.

Перше рівняння – функція споживання, друге рівняння – функція інвестицій, третє рівняння – функція грошового ринку, четверте рівняння – тотожність прибутку.

Модель являє собою систему одночасних рівнянь, кожне з яких перевіряється на ідентифікацію.

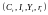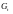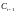Модель включає чотири ендогенні змінні і чотири незалежні змінні (екзогенні змінні і , лагові змінні і ).

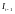Необхідно перевірити умову ідентифікації для кожного із рівнянь моделі.

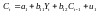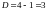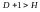Перше рівняння: . Рівняння містить дві ендогенні змінні C_t і Y_t і одну незалежну змінну C_t-1. Отже, Н = 2, , тобто виконується умова . Рівняння надідентифіковане.

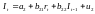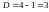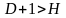Друге рівняння: . Рівняння містить дві ендогенні змінні I_t і r_t (Н = 2) і одну екзогенну змінну I_t-1 ( ). Виконується умова . Рівняння надідентифіковане.

Третє рівняння: 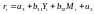. Рівняння містить дві ендо­генні змінні I_t і r_t і одну екзогенну змінну . Виконується умова . Рівняння надідентифіковане.

Четверте рівняння: 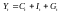. Рівняння являє собою тотож­ність, параметри якої відомі. Необхідності в ідентифікації немає.

Для кожного рівняння перевіряється достатня умова ідентифі­кації. Для цього складається матриця коефіцієнтів при змінних моделі.

Згідно з достатньою умовою ідентифікації визначник матриці коефіцієнтів при змінних, що не входять в досліджуване рівняння, не повинен дорівнювати 0, а ранг матриці повинен дорівнювати числу ендогенних змінних моделі мінус 1, тобто 4 – 1 = 3.

1 рівняння	–1	0	0			0	0	0
2 рівняння	0	–1		0	0		0	0
3 рівняння	0	0	–1		0	0		0
Тотожність	1	1	0	–1	0	0	0	1

Перше рівняння. Матриця коефіцієнтів при змінних, що не входять в рівняння, має вигляд:

2 рівняння	–1			0	0
3 рівняння	0	–1	0		0
Тотожність	1	0	0	0	1

Ранг даної матриці дорівнює трьом, оскільки існує квадратна підматриця даної матриці 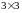, визначник якої не дорівнює нулю:

.

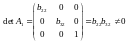Для даного рівняння достатня умова ідентифікації виконується.

Друге рівняння. Матриця коефіцієнтів при змінних, що не входять в рівняння, має вигляд:

1 рівняння	–1			0	0
3 рівняння	0		0		0
Тотожність	1	–1	0	0	1

Ранг даної матриці дорівнює трьом, оскільки існує квадратна підматриця даної матриці 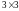, визначник якої не дорівнює нулю:

.

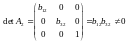Для даного рівняння достатня умова ідентифікації виконується.

Третє рівняння. Матриця коефіцієнтів при змінних, що не входять в рівняння, має вигляд:

1 рівняння	–1	0		0	0
2 рівняння	0	–1	0		0
Тотожність	1	1	0	0	1

Ранг даної матриці дорівнює трьом, оскільки існує квадратна підматриця даної матриці 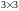, визначник якої не дорівнює нулю:

.

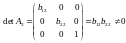Для даного рівняння достатня умова ідентифікації виконується.

Таким чином, всі рівняння моделі надідентифіковані. Для оцінки параметрів кожного рівняння доцільно застосовувати двокроковий МНК.