Контрольні питання

1. Охарактеризувати методи побудови багатофакторної регресійної моделі.

32. Навести загальний вигляд рівняння регресії в стандартизованому масштабі. Як пов’язані коефіцієнти “чистої” регресії з коефіцієнтами стандартизованої регресії?

33. Що показує коефіцієнт детермінації? Як він розраховується? У яких межах знаходяться його значення?

34. Що показує множинний коефіцієнт кореляції? Як він розраховується?

35. Що характеризують парні коефіцієнти кореляції?

36. Показати залежність між F-критерієм і R²?

37. Що таке стандартна помилка оцінок параметрів моделі?

38. Що означає мультиколінеарність змінних? Ознаки мультиколінеарності.

39. До яких наслідків призводить мультиколінеарність?

40. Як впливає мультиколінеарність на оцінку параметрів моделі?

41. Які статистичні критерії використовують для визначення мультиколінеарності?

42. Коротко охарактеризувати алгоритм Фаррара–Глобера.

43. Методи усунення мультиколінеарності.

44. Сутність методу головних компонент.

45. Коли доцільно застосовувати метод головних компонент?

Лабораторна робота № 3 (4 години) Тема. Дослідження гетероскедастичності та автокореляції залишків з використанням засобів ms Excel

Мета роботи: набуття навичок застосування тесту Гольдфельда–Квандта для виявлення гетероскедастичності та оцінки параметрів економетричної моделі методом Ейткена; виявлення автокореляції залишків та оцінка параметрів моделі з автокорельованими залишками.

Завдання 1

Дослідити залежність продуктивності праці Y (т/год.) від рівня механізації робіт Х₁ (%), середнього віку робітників Х₂ (років) і енергоозброєності Х₃ (КВт на 100 працюючих) за даними 14 промислових підприємств (табл. Б.1). Необхідно:

1. Перевірити гіпотезу про наявність гетероскедастичності для вхідних даних.

46. Оцінити параметри моделі за методом 1МНК і методом Ейткена.

47. Перевірити істотність зв’язку, що описується моделями, оцінки параметрів яких розраховані за методом 1МНК і методом Ейткена.

48. Дати порівняльний аналіз оцінок параметрів, отриманих різними методами, зробити висновки.

Порядок виконання завдання

1. Згідно з номером варіанта обрати умову задачі.

2. Дослідити наявність гетероскедастичності, скориставшись тестом Гольдфельда–Квандта.

3. Знайти оцінки параметрів лінійної регресії, використовуючи метод найменших квадратів.

4. Знайти оцінки параметрів лінійної регресії, використовуючи метод Ейткена.

5. Перевірити істотність зв’язку, що описується побудованими моделями, визначивши коефіцієнти детермінації та кореляції.

6. Дати порівняльний аналіз оцінок параметрів, отриманих різними методами.

Завдання 2

Для моделі, що була побудована в завданні 1, встановити, чи існує автокореляція залишків.

Порядок виконання завдання

1. За результатами рішення завдання 1 обрати кращу із побудованих моделей з використанням 1МНК чи методу Ейткена.

2. Перевірити наявність автокореляції залишків, використовуючи циклічний коефіцієнт кореляції.

3. Перевірити наявність автокореляції залишків, використовуючи критерій Дарбіна–Уотсона.

4. Зробити висновки.

Вимоги до оформлення звіту

Звіт про виконання даної лабораторної роботи оформлюється в окремому зошиті згідно з встановленими вимогами до оформлення звітів і містить:

• назву, тему, завдання, опис мети лабораторної роботи;

• вихідні дані варіанта;

• рішення поставлених завдань з використанням формул, що супроводжуються коментарями;

• висновки.

Зразок виконання лабораторної роботи

Завдання 1

Для перевірки гіпотези про наявність гетероскедастичності вихідних даних використати тест Гольдфельда–Квандта. У множинній регресії даний тест може проводитися для кожної із пояснюючих змінних. Перед початком рішення завдання вихідні дані упорядкувати за зростанням змінної Х₁ (табл. Д.1).

Далі визначити C спостережень, які знаходяться в середині сукупності:

.

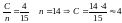Тоді .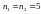

Побудувати економетричну модель для кожної із сукупностей . Для сукупності 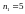оцінити параметри моделі на основі 1МНК (табл. В.1).

Для цього скласти вектор – стовпець Y₁ і матрицю Х₁:

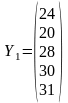
Одиничний стовпець в матриці незалежних змінних Х дописується тоді, коли економетрична модель має вільний член а₀.

Обчислити оцінки регресійних коефіцієнтів за формулою:

.

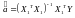Для даного прикладу:

	1	1	1	1	1
Х1Т =	30	32	36	40	41
	31	33	41	39	46
	290	300	350	400	400

	5	179	190	1 740
Х1ТХ1 =	179	6 501	6 908	63 300
	190	6 908	7 368	67 240
	1740	63 300	67 240	616 600

	35,035	6,218	0,653	0,468
(Х1ТХ1)-1 =	–6,218	1,633	–0,193	–0,129
	0,653	–0,193	0,052	0,012
	0,468	–0,129	0,012	0,011

	133
Х1ТY1 =	4 839
	5 148
	47 160

Тоді :

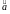	15,67
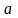=	–4,47
	0,68
	0,42

Регресійна модель для першої вибірки має вигляд: 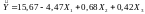. Аналогічно будуємо регресійну модель для другої вибірки і в результаті отримуємо: .

Для кожної з розрахованих моделей знайти суму квадратів залишків:

,

.

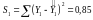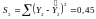Розрахувати критерій .

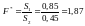Порівняти цей критерій із табличним значенням критерію Фішера при ступенях свободи 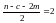і рівні довіри  = 0,05 F_табл = 19,00. Гетероскедастичність відсутня, тому що .

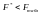Хоча гетероскедастичність відсутня, проводиться оцінка параметрів моделі за допомогою 1МНК та методу Ейткена та порівнюються отримані результати.

За допомогою 1МНК обчислити оцінки регресійних коефіцієнтів за формулою .

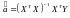Для даного прикладу .

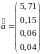Розрахувати коефіцієнт детермінації для побудованої моделі, який дорівнює 0,951. Оскільки він наближається до одиниці, варіація залежної змінної в основному визначається варіацією незалежних змінних. Коефіцієнт кореляції також великий (R = 0,975), тому існує досить тісний лінійний зв’язок усіх незалежних факторів із залежною змінною Y. Залишкова дисперсія при цьому дорівнює 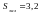. Тобто побудована модель добре описує вихідні дані.

Для знаходження оцінок параметрів моделі застосувати метод Ейткена. Оператор оцінювання параметрів УМНК .

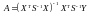Діагональна матриця S записується так:

.

Згідно з першою гіпотезою припустимо, що елементи 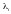пропорційні до зміни пояснювальної змінної Х_і1 , тобто 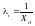(Х_і1 – рівень механізації робіт за і-м спостереженням). Тоді матриця S записується у вигляді:

	30	0	0	0	0	0	0	0	0	0	0	0	0	0
	0	32	0	0	0	0	0	0	0	0	0	0	0	0
	0	0	36	0	0	0	0	0	0	0	0	0	0	0
	0	0	0	40	0	0	0	0	0	0	0	0	0	0
	0	0	0	0	41	0	0	0	0	0	0	0	0	0
S =	0	0	0	0	0	47	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	56	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	54	0	0	0	0	0	0
	0	0	0	0	0	0	0	0	60	0	0	0	0	0
	0	0	0	0	0	0	0	0	0	55	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	61	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	67	0	0
	0	0	0	0	0	0	0	0	0	0	0	0	69	0
	0	0	0	0	0	0	0	0	0	0	0	0	0	76

Оцінка параметрів моделі за методом Ейткена:

.

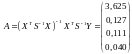Економетрична модель залежності продуктивності праці від рівня механізації робіт, середнього віку робітників та енергоозброєності для теоретичних даних запишеться так:

.

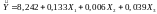Коефіцієнт детермінації для побудованої моделі з використанням методу Ейткена дорівнює 0,996, що майже не відрізняється від 1МНК. Однак коефіцієнт детермінації не може повною мірою задовольнити якість моделі при застосуванні УМНК. Тому потрібно звернути увагу на значення залишкової дисперсії: 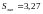. При використанні обох методів значення залишкових дисперсій майже однакові. Отже, використання методу Ейткена не покращує модель. Це можна пояснити тим, що вихідні дані є гомоскедастичними.