Завдання 2

При дослідженні мультиколінеарності було прийнято рішення про виключення фактора енергоозброєності з моделі (Х₃). Тому побудова множинної лінійної регресії буде проводитися з урахуванням тільки рівня механізації (Х₁) та середнього віку робітників (Х₂). Тобто розглядається просторова вибірка об’єму n = 20, число пояснюючих змінних k = 2.

Проводиться специфікація моделі у вигляді лінійної функції 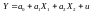. Звідси випливає, що система нормальних рівнянь для моделі буде мати вигляд:

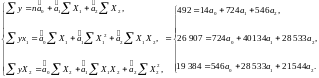
Таблиця 2.2

Допоміжні розрахунки

№ пор.	Y	X1	X2	Y2	X12	X22	YX1	YX2	X1X2
1	20	32	33	400	1 024	1 089	640	660	1 056
2	24	30	31	576	900	961	720	744	930
3	28	36	41	784	1 296	1 681	1 008	1 148	1 476
4	30	40	39	900	1 600	1 521	1 200	1 170	1 560
5	31	41	46	961	1 681	2 116	1 271	1 426	1 886
6	33	47	43	1 089	2 209	1 849	1 551	1 419	2 021
7	34	56	34	1 156	3 136	1 156	1 904	1 156	1 904
8	37	54	38	1 369	2 916	1 444	1 998	1 406	2 052
9	38	60	42	1 444	3 600	1 764	2 280	1 596	2 520
10	40	55	35	1 600	3 025	1 225	2 200	1 400	1 925
11	41	61	39	1 681	3 721	1 521	2 501	1 599	2 379
12	43	67	44	1 849	4 489	1 936	2 881	1 892	2 948
13	45	69	40	2 025	4 761	1 600	3 105	1 800	2 760
14	48	76	41	2 304	5 776	1 681	3 648	1 968	3 116
Сума	492	724	546	1 8138	40 134	21 544	2 6907	19 384	28 533
Середнє	35,14	51,71	39,00	1 295,6	2 866,7	1 538,9	1 921,9	1 384,6	2 038,07
σ	8,08	14,39	4,39	–	–	–	–	–	–
σ2	65,21	207,14	19,23	–	–	–	–	–	–

Для рішення системи рівнянь використовується метод визначників.

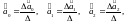
де 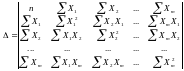– визначник системи;

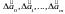– часткові визначники, що отримані шляхом заміни відповідного стовпця матриці визначника системи даними лівої частини системи.

,

,

,

.

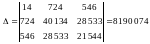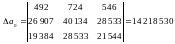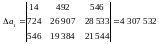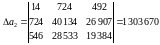Тоді

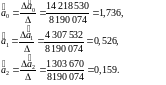
Рівняння регресії має вигляд: .

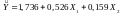Інший вид рівняння множинної регресії – рівняння регресії в стан­дартизованому масштабі: 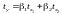. Коефіцієнти стандартизованого рівняння регресії можна розрахувати так:

.

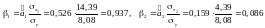Рівняння регресії в стандартизованому вигляді: 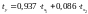. Тобто зі збільшенням рівня механізації на одну сигму при незмінному середньому віці робітників продуктивність праці збільшується в середньому на 0,937 сігми. Оскільки 0,937 > 0,086, то вплив рівня механізації на продуктивність праці більший, ніж середній вік робітників.

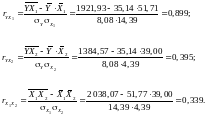
Коефіцієнти парної кореляції показують на тісний зв’язок фактора Х₁ з результатом, фактор Х₂ має помірну силу зв’язку. Міжфакторна залежність є помірною, тобто фактори Х₁ та Х₂ не є колінеарними.

Часткові коефіцієнти кореляції характеризують тісноту зв’язку між результатом і відповідним фактором при виключенні впливу інших факторів, включених у рівняння регресії:

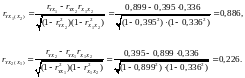
Як бачимо, зв’язок рівня механізації з продуктивністю праці при виключенні впливу середнього віку робітників тісний, на відміну від зв’язку останнього з продуктивністю праці.

Коефіцієнт детермінації для даної залежності:

.

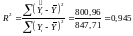Коефіцієнт детермінації показує, що продуктивність праці на 94,5 % описується вибраним набором факторів.

Скоригований коефіцієнт детермінації розраховується за формулою:

.

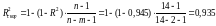Скоригований коефіцієнт детермінації визначає тісноту зв’язку з врахуванням ступенів свободи загальної і залишкової дисперсії. Він дає таку оцінку зв’язку, яка не залежить від числа факторів і тому може порівнюватися за різними моделями і різним числом факторів. Обидва коефіцієнти вказують на досить високу (більшу 90 %) детермінованість результату Y в моделі факторами X₁ і X₂.

Для характеристики тісноти зв’язку в множинній лінійній регресії використовують множинний коефіцієнт кореляції:

.

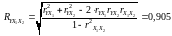Розраховане значення коефіцієнта множинної кореляції свідчить про достатньо тісний зв’язок факторів з результатом.

Оцінку надійності рівняння регресії в цілому і показника тісноти зв’язку показує F-критерій Фішера:

.

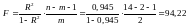Отже, 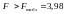(при n = 14), тобто ймовірність випадково отримати таке значення F-критерію не перевищує допустимий рівень значимості (5 %).

Для визначення статистичної значимості оцінок параметрів рівняння регресії необхідно скористатися формулою для розрахунку t-критерію Ст’юдента:

,

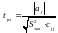де а_j – параметри рівняння регресії;

с_jj – діагональний елемент матриці ;

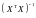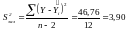– залишкова дисперсія.

Для розрахунку за даною формулою виконуються допоміжні розрахунки.

Матриця Х для даної моделі буде такою:

	1	32	33
	1	30	31
	1	36	41
	1	40	39
	1	41	46
	1	47	43
Х =	1	56	34
	1	54	38
	1	60	42
	1	55	35
	1	61	39
	1	67	44
	1	69	40
	1	76	41

Одиниця в матриці незалежних змінних Х дописується тоді, коли економетрична модель має вільний член а₀.

Тоді Х^Т:

	1	1	1	1	1	1	1	1	1	1	1	1	1	1
ХТ =	32	30	36	40	41	47	56	54	60	55	61	67	69	76
	33	31	41	39	46	43	34	38	42	35	39	44	40	41

Звідси :

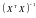	6,1678	–0,0023	–0,1533
(ХТХ)-1 =	–0,0023	0,0004	–0,0005
	–0,1533	–0,0005	0,0046

,

,

.

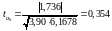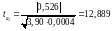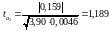Табличне значення критерію Ст’юдента при рівні значимості α = 0,05 та числі ступенів свободи (n – m – 1) = (14 – 3) = 11 вибрати t_табл = 2,201.

Тоді 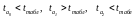, тобто статистично значимим параметром рівняння регресії є лише а₁.

На основі критеріїв Ст’юдента та стандартної помилки можуть бути визначені довірчі інтервали для параметрів моделі:

,

,

.

,

,

.

,

,

.

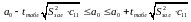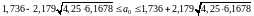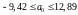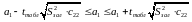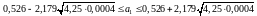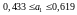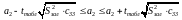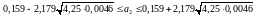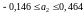Аналіз верхньої та нижньої межі довірчих інтервалів зумовлює висновок про те, що з ймовірністю 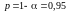параметри а₀ і а₂, знаходячись у вказаних межах, приймають нульові значення, тобто є статистично незначимими. Параметр а₁ є статистично значимий.

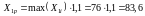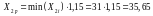Якщо прогнозоване значення рівня механізації складе %, а середній вік робітників , то прогнозоване значення продуктивності праці становить: 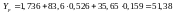т/год.

Правильність розрахунків перевіримо за допомогою надбудови Анализ данных в MS Excel:

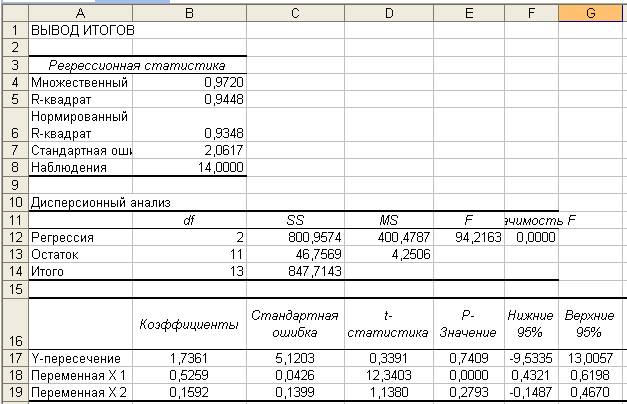
Рис. 2.2. Результат виконання інструменту Анализ данных/Регрессия

Перевірка результатів розрахунків з використанням пакета Statistica проводиться аналогічно до лабораторної роботи № 1.