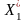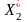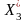- •Економіко-математичні методи і моделі: економетрика
- •Лабораторна робота № 1 (2 години) Тема. Побудова та аналіз функції парної лінійної регресії з використанням засобів ms Excel та пакета Statistica
- •Завдання 1
- •Порядок виконання лабораторної роботи
- •Вимоги до оформлення звіту
- •Зразок виконання лабораторної роботи
- •Контрольні питання
- •Вимоги до оформлення звіту
- •Зразок виконання лабораторної роботи Завдання 1
- •Завдання 2
- •Контрольні питання
- •Лабораторна робота № 3 (4 години) Тема. Дослідження гетероскедастичності та автокореляції залишків з використанням засобів ms Excel
- •Завдання 1
- •Порядок виконання завдання
- •Завдання 2
- •Контрольні питання
- •Контрольні питання
- •Лабораторна робота № 5 (4 години) Тема. Модель часових рядів: виділення тренду та сезонних коливань з використанням пакета Statistica
- •Завдання 1
- •Вимоги до оформлення звіту
- •Зразок виконання лабораторної роботи
- •К онтрольні питання
- •Список рекомендованої літератури
- •Додаток а Вихідні дані для лабораторної роботи № 1
- •Додаток б Вихідні дані для лабораторної роботи № 2 та № 3
- •Додаток в Вихідні дані для лабораторної роботи № 4
- •Додаток г Вихідні дані до лабораторної роботи № 5
- •Економіко-математичні методи і моделі: економетрика
Вимоги до оформлення звіту
Звіт про виконання даної лабораторної роботи оформлюється в окремому зошиті згідно з встановленими вимогами до оформлення звітів і містить:
назву, тему, завдання, опис мети лабораторної роботи;
вихідні дані варіанта;
рішення поставлених завдань з використанням формул, що супроводжуються коментарями;
результати інструменту Регрессия надбудови Анализ данных в MS Excel;
короткий опис технології рішення задачі в пакеті Statistica;
результати рішення поставлених завдань в пакеті Statistica;
висновки.
Зразок виконання лабораторної роботи Завдання 1
Дослідити залежність продуктивності праці Y (т/год.) від рівня механізації робіт Х1 (%), середнього віку робітників Х2 (років) і енергоозброєності Х3 (КВт на 100 працюючих) за даними 14 промислових підприємств.
Таблиця 2.1
Проміжні розрахунки
№ пор. |
Y |
X1 |
X2 |
X3 |
|
|
|
1 |
20 |
32 |
33 |
300 |
388,65 |
36,00 |
43 502,04 |
2 |
24 |
30 |
31 |
290 |
471,51 |
64,00 |
47 773,47 |
3 |
28 |
36 |
41 |
350 |
246,94 |
4,00 |
25 144,90 |
4 |
30 |
40 |
39 |
400 |
137,22 |
0,00 |
11 787,76 |
5 |
31 |
41 |
46 |
400 |
114,80 |
49,00 |
11 787,76 |
6 |
33 |
47 |
43 |
480 |
22,22 |
16,00 |
816,33 |
7 |
34 |
56 |
34 |
500 |
18,37 |
25,00 |
73,47 |
8 |
37 |
54 |
38 |
520 |
5,22 |
1,00 |
130,61 |
9 |
38 |
60 |
42 |
590 |
68,65 |
9,00 |
6 630,61 |
10 |
40 |
55 |
35 |
540 |
10,80 |
16,00 |
987,76 |
11 |
41 |
61 |
39 |
600 |
86,22 |
0,00 |
8 359,18 |
12 |
43 |
67 |
44 |
700 |
233,65 |
25,00 |
36 644,90 |
13 |
45 |
69 |
40 |
700 |
298,80 |
1,00 |
36 644,90 |
14 |
48 |
76 |
41 |
750 |
589,80 |
4,00 |
58 287,76 |
Сума |
492,00 |
724,00 |
546,00 |
7 120,00 |
2 692,86 |
250,00 |
28 8571,43 |
Середнє |
35,14 |
51,71 |
39,00 |
508,57 |
192,35 |
17,86 |
20 612,24 |
|
8,08 |
14,39 |
4,39 |
148,99 |
– |
– |
– |
|
65,21 |
207,14 |
19,23 |
22 197,80 |
– |
– |
– |
Обчислити середні
значення та стандартні відхилення
пояснюючих змінних
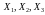 .
Для цього можна скористатися стандартними
функціями MS Excel (СРЗНАЧ та СТАНДОТКЛОН).
.
Для цього можна скористатися стандартними
функціями MS Excel (СРЗНАЧ та СТАНДОТКЛОН).
Дані величини можна також розрахувати за формулами:
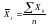 ,
,
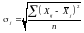 ,
,
де 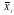 – середнє
значення
– середнє
значення
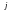 -ї
пояснюючої змінної;
-ї
пояснюючої змінної;
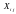 – індивідуальне
значення
-ї
пояснюючої змінної;
– індивідуальне
значення
-ї
пояснюючої змінної;
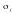 – стандартне
відхилення
-ї
пояснюючої змінної;
– стандартне
відхилення
-ї
пояснюючої змінної;
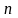 – число
спостережень.
– число
спостережень.
За алгоритмом
методу Фаррара–Глобера перший крок –
це нормалізація значень факторів.
Нормалізувати
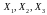 ,
використавши нижченаведену формулу
або функцію НОРМАЛИЗАЦИЯ.
,
використавши нижченаведену формулу
або функцію НОРМАЛИЗАЦИЯ.

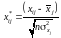 ,
,
|
|
|
|
–0,366 |
–0,366 |
–0,374 |
|
–0,403 |
–0,488 |
–0,392 |
|
–0,292 |
0,122 |
–0,284 |
|
–0,218 |
0,000 |
–0,195 |
|
–0,199 |
0,427 |
–0,195 |
|
–0,088 |
0,244 |
–0,051 |
|
0,080 |
–0,305 |
–0,015 |
|
0,042 |
–0,061 |
0,021 |
|
0,154 |
0,183 |
0,146 |
|
0,061 |
–0,244 |
0,056 |
|
0,172 |
0,000 |
0,164 |
|
0,284 |
0,305 |
0,343 |
|
0,321 |
0,061 |
0,343 |
|
0,451 |
0,122 |
0,433 |
Другим кроком є розрахунок кореляційної матриці R за формулою:
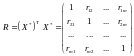 ,
,
де 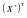 – транспонована
матриця Х*.
Елементи матриці R
характеризують щільність зв’язку
однієї незалежної змінної з іншою;
– транспонована
матриця Х*.
Елементи матриці R
характеризують щільність зв’язку
однієї незалежної змінної з іншою;
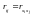 – парні
коефіцієнти кореляції.
– парні
коефіцієнти кореляції.
Транспортувати
матрицю
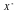 (нормалізовану)
в матрицю
(нормалізовану)
в матрицю
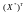 .
Тоді, перемноживши матриці
та
,
отримаємо:
.
Тоді, перемноживши матриці
та
,
отримаємо:
|
0,93 |
0,34 |
0,92 |
R = |
0,34 |
0,93 |
0,39 |
|
0,92 |
0,39 |
0,93 |
Як бачимо, діагональні елементи матриці R не дорівнюють одиниці. Отже, необхідно штучно проставити на діагоналі матриці одиниці, а до решти елементів додати різницю між одиницею й значенням діагонального елемента:
|
1 |
0,41 |
0,99 |
R = |
0,41 |
1 |
0,46 |
|
0,99 |
0,46 |
1 |
Визначаємо значення
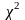 :
:
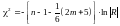 ,
,
де 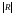 – визначник кореляційної матриці R.
– визначник кореляційної матриці R.
Перш за все необхідно
визначити визначник кореляційної
матриці, для чого можна скористатися
функцією MS Excel МОПРЕД. У результаті
отримаємо:
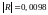 .
.
Оскільки наближається до нуля, то в масиві пояснюючих змінних може існувати мультиколінеарність.
Прологарифмуємо
визначник матриці R:
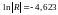 .
.
Тоді
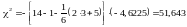 .
Порівнюємо
.
Порівнюємо
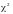 з табличним значенням при
з табличним значенням при
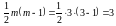 ступенях свободи і рівні значимості
α = 0,05. Оскільки
ступенях свободи і рівні значимості
α = 0,05. Оскільки
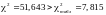 ,
то в масиві незалежних змінних (рівень
механізації, середній вік робітників,
енергоозброєність) існує мультиколінеарність.
,
то в масиві незалежних змінних (рівень
механізації, середній вік робітників,
енергоозброєність) існує мультиколінеарність.
Для визначення F-критеріїв необхідно знайти матрицю похибок С, яка є оберненою до матриці R:
 .
.
Безпосередньо F-критерій обчислюється за формулою:
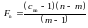 ,
,
де 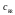 – діагональні елементи матриці С;
– діагональні елементи матриці С;
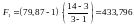 ,
,
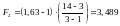 ,
,
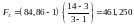 .
.
Обчислені критерії
порівняти з табличним значенням
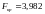 ,
при k1 = m – 1 = 3 – 1 = 2,
k2 = n – m = 14 – 3 = 11
ступенів свободи та при рівні значущості
.
,
при k1 = m – 1 = 3 – 1 = 2,
k2 = n – m = 14 – 3 = 11
ступенів свободи та при рівні значущості
.
У даному випадку
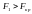 ,
,
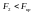 ,
,
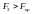 .
Це означає, що перша і третя змінні
мультиколінеарні з іншими.
.
Це означає, що перша і третя змінні
мультиколінеарні з іншими.
Розрахувати часткові коефіцієнти кореляції, які характеризують тісноту зв’язку між двома змінними за умови, що інші змінні не впливають на цей зв’язок (існування парної мультиколінеарності):
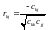 ,
,
де 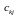 – елементи
матриці С,
що розміщені в k-му
рядку та j-му
стовпці;
– елементи
матриці С,
що розміщені в k-му
рядку та j-му
стовпці;
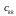 і
і
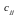 – діагональні
елементи матриці С.
– діагональні
елементи матриці С.
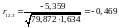 ,
,
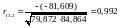 ,
,
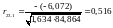 .
.
Отже, спираючись на отримані значення часткових коефіцієнтів кореляції, можна відмітити, що зв’язок між рівнем механізації та середнім віком робітників помірний, якщо не враховувати вплив енергоозброєності. Зв’язок між рівнем механізації та енергоозброєністю є досить тісним, якщо не брати до уваги вплив середнього віку робітників. Зв’язок між середнім віком робітників та енергоозброєністю середній, якщо не враховувати рівень механізації.
Розрахувати t-критерії, які застосовуються для визначення мультиколінеарності двох пояснюючих змінних і обчислюються за формулою:
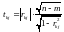 .
.
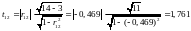 ,
,
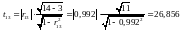 ,
,
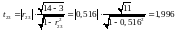 .
.
Обчислені t-критерії
порівнюються з табличним значенням
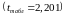 ,
коли маємо
,
коли маємо
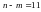 ступенів свободи, та при рівні значущості
.
ступенів свободи, та при рівні значущості
.
Оскільки
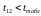 ,
то між рівнем механізації та середнім
віком робітників мультиколінеарності
не існує;
,
то між рівнем механізації та середнім
віком робітників мультиколінеарності
не існує;
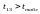 ,
тому відповідно між рівнем механізації
та енергоозброєністю існує
мультиколінеарність;
,
тому відповідно між рівнем механізації
та енергоозброєністю існує
мультиколінеарність;
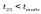 ,
тому між середнім віком робітників та
енергоозброєністю мультиколінеарності
не існує.
,
тому між середнім віком робітників та
енергоозброєністю мультиколінеарності
не існує.
Дослідження, проведені за алгоритмом Фаррара–Глобера, показали, що мультиколінеарність між пояснюючими змінними даного прикладу існує. Отже, для того, щоб можна було застосувати метод 1МНК для оцінювання параметрів моделі за цією інформацією, необхідно в першу чергу звільнитися від мультиколінеарності. Приймається рішення про виключення фактора Х3 з подальших досліджень.
Перевірити отримані результати та зроблені висновки з використанням надбудови Анализ данных / Корреляция в MS Excel. Матриця парних коефіцієнтів кореляції між факторами:
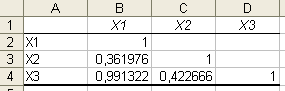
Рис. 2.1. Матриця парних коефіцієнтів кореляції
Визначник матриці парних коефіцієнтів кореляції між чинниками дорівнює 0,0098. Величина визначника матриці міжфакторних коефіцієнтів кореляції наближається до нуля, що свідчить про високий ступінь мультиколінеарності факторів. Значення парних коефіцієнтів кореляції, що перевищує 0,75, вказує на колінеарні фактори. Для уточнення внеску кожного фактора в мультиколінеарність розраховуються коефіцієнти множинної детермінації (Анализ данных / Регрессия).
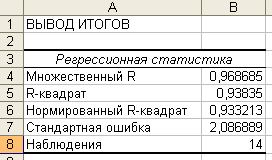
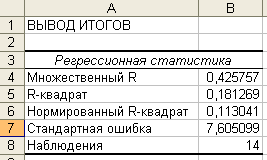
Коефіцієнти множинної детермінації:
для Х1:
для Х2:
для Х3:
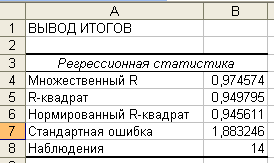
Низьке значення визначника матриці міжфакторних кореляцій і високі значення коефіцієнтів множинної детермінації для Х1 та Х3 свідчать про наявність мультиколінеарності.

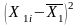
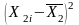
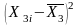
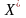 =
=