Контрольні питання

1. Яка модель належить до категорії економетричних? Що таке загальна модель, лінійна модель?

9. Як записується економетрична модель у загальному вигляді? Які змінні у моделі є ендогенними, а які екзогенними?

10. Теоретичне та емпіричне рівняння лінійної регресії. Сутність параметрів рівняння регресії.

11. Чому у модель фактичних даних вводиться випадкова складова u?

12. Які етапи побудови економетричної моделі?

13. Що таке специфікація економетричної моделі?

14. Сутність методу найменших квадратів 1 МНК.

15. За яких умов неможливе використання 1 МНК?

16. Що таке гомоскедастичність? При порушенні якої умови застосування 1 МНК має місце гомоскедастичність?

17. Що таке мультиколінеарність? При порушенні якої умови застосування 1 МНК має місце мультиколінеарність?

18. Сутність кореляційного та регресійного аналізу.

19. Побудова точкового та інтервального прогнозу залежної змінної в моделі парної лінійної регресії.

20. Сутність та допустимі значення коефіцієнта детермінації:

21. Сутність коефіцієнта кореляції. Пряма та обернена кореляція.

22. У яких межах має знаходитися похибка апроксимації для того, щоб можна було зробити висновок про “гарну” якість моделі?

ЛАБОРАТОРНА РОБОТА № 2 (4 години)

Тема. Побудова та аналіз функції множинної лінійної регресії з використанням засобів MS Excel та пакета Statistica

Мета роботи: набуття навичок побудови моделі множинної лінійної регресії з урахуванням лише неколінеарних факторів, оцінка якості моделі.

Завдання 1

Дослідити залежність продуктивності праці Y (т/год.) від рівня механізації робіт Х₁ (%), середнього віку робітників Х₂ (років) і енергоозброєності Х₃ (КВт на 100 працюючих) за даними 14 промислових підприємств (табл. Б.1). Необхідно:

1. Дослідити наявність мультиколінеарності між пояснюючими змін­ними, скориставшись алгоритмом Фаррара–Глобера.

Порядок виконання завдання

1. Згідно з номером варіанта обрати умову задачі.

2. Дослідити наявність мультиколінеарності між пояснюючими змін­ними, скориставшись алгоритмом Фаррара–Глобера.

3. Розрахунки підтвердити з використанням засобів MS Excel.

4. Розв’язок задачі необхідно супроводжувати коментарями з наведенням формул, результатів обчислень та висновків за цими результатами.

Завдання 2

На основі рішення завдання 1 побудувати та дослідити рівняння множинної лінійної регресії, включивши лише неколінеарні фактори.

Порядок виконання завдання

1. Вихідні дані взяти із завдання 1, включивши лише неколінеарні фактори.

23. На основі статистичних даних показника Y та незалежних факторів знайти оцінки параметрів множинної регресії, використовуючи метод найменших квадратів. Записати “чисте” рівняння регресії та в стандартизованому вигляді.

24. Визначити часткові коефіцієнти кореляції та оцінити їх значимість.

25. Визначити множинні коефіцієнти кореляції та детермінації. Порівняти загальний коефіцієнт множинної детермінації зі скоригованим.

26. За допомогою F-критерію Фішера оцінити статистичну значимість зв’язку між факторами.

27. Оцінити статистичну значимість параметрів регресії з використання t-критерію Ст’юдента для рівня значимості .

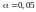28. Знайти довірчі інтервали для коефіцієнтів регресії для рівня значимості .

29. Зробити точковий прогноз залежної змінної при значенні пояснюючої змінної Х₁, що рівне максимальному спостереженню, збільшеному на 10 %, та значенні змінної Х₂, що дорівнює мінімальному значенню, збільшеному на 15 %.

30. Розрахунки підтвердити розрахунками в пакеті Statistica.

31. Розв’язок задачі необхідно супроводжувати коментарями з наведенням формул, результатів обчислень та висновків за цими результатами.

Для вирішення завдань використати: інструктивні матеріали, надбудову Анализ данных в MS Excel, Multiple Regression в пакеті Statistica.