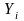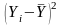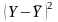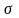Лабораторна робота № 1 (2 години) Тема. Побудова та аналіз функції парної лінійної регресії з використанням засобів ms Excel та пакета Statistica

Мета лабораторної роботи: набуття навичок побудови моделі парної лінійної регресії, оцінка її параметрів методом найменших квадратів (1МНК), дослідження моделі.

Завдання 1

Дослідити залежність продуктивності праці Y (т/год.) від рівня механізації робіт Х (%) за даними 14 промислових підприємств (табл. А.1). Необхідно:

1. На основі статистичних даних показника Y та фактора Х знайти оцінки параметрів лінійної регресії, використовуючи метод найменших квадратів.

2. Побудувати поле кореляції та графік лінії регресії.

3. Оцінити тісноту зв’язку між залежною змінною Y та незалежною змінною Х.

4. Використовуючи F-критерій Фішера, з надійністю р = 0,95 оцінити адекватність побудованої моделі щодо статистичних даних.

5. Знайти середню похибку апроксимації і стандартні похибки оцінок коефіцієнтів регресії.

6. Оцінити статистичну значимість параметрів регресії з використання t-критерію Ст’юдента для рівня значимості .

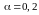7. Знайти довірчі інтервали для коефіцієнтів регресії для рівня значимості .

8. Зробити точковий та інтервальний прогноз залежної змінної при значенні пояснюючої змінної, що дорівнює максимальному спостереженню, збільшеному на 10 %. Відобразити їх на полі кореляції.

Порядок виконання лабораторної роботи

1. Згідно з номером варіанта обрати умову задачі та побудувати модель парної лінійної регресії, використовуючи метод найменших квадратів (1МНК).

2. Дослідити модель, використовуючи формули, та перевірити результати розрахунків за допомогою надбудови MS Excel Анализ данных.

3. Розрахунки підтвердити розрахунками в пакеті Statistica, крім пунктів 6 та 7.

4. Розв’язок задачі необхідно супроводжувати коментарями з наведенням формул, результатів обчислень та висновків за цими результатами.

Для вирішення задачі використати інструктивні матеріали, надбудову Анализ данных в MS Excel, Multiple Regression в пакеті Statistica.

Вимоги до оформлення звіту

Звіт про виконання даної лабораторної роботи оформляється в окремому зошиті згідно з встановленими вимогами до оформлення звітів і містить:

• назву, тему, завдання, опис мети лабораторної роботи;

• вихідні дані варіанта;

• рішення поставлених завдань з використанням формул, що супроводжуються коментарями;

• результати інструменту Регрессия надбудови Анализ данных в MS Excel;

• результати рішення поставлених завдань в пакеті Statistica;

• висновки.

Зразок виконання лабораторної роботи

Досліджується залежність продуктивності праці Y (т/год.) від рівня механізації робіт Х (%) за даними 14 промислових підприємств (табл. 1.1).

Таблиця 1.1

№ пор.	Х	Y	XY	X2	Y2				Аі
1	11	8	88	121	64	13,40	107,83	249,19	67,52
2	20	23	460	400	529	17,12	44,45	0,62	25,57
3	55	29	1 595	3 025	841	31,57	60,66	27,19	8,88
4	35	25	875	1 225	625	23,31	0,22	1,47	6,75
5	70	35	2 450	4 00	1 225	37,77	195,53	125,76	7,91
6	25	17	425	625	289	19,18	21,18	46,05	12,84
7	62	30	1 860	3 844	900	34,46	114,05	38,62	14,88
8	34	25	850	1 156	625	22,90	0,78	1,47	8,40
9	15	20	300	225	400	15,05	76,25	14,33	24,73
10	20	20	400	400	400	17,12	44,45	14,33	14,41
11	88	52	4 576	7 744	2 704	45,20	458,71	796,05	13,07
12	10	13	130	100	169	12,99	116,58	116,33	0,09
13	11	11	121	121	121	13,40	107,83	163,47	21,83
14	50	25	1 250	2 500	625	29,51	32,75	1,47	18,04
Сума	506	333	15 380	26 386	9 517	333	1 381,28	1 596,36	244,9
Сер.	36,14	23,79	1 098,6	1 884,7	679,8	–	–	–	17,49
	24,96	11,08	–	–	–	–	–	–	–
	622,9	122,8	–	–	–	–	–	–	–

Згідно з 1МНК необхідно записати систему нормальних рівнянь для даного прикладу:

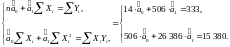
Поділивши обидва рівняння системи на n = 14, отримаємо:

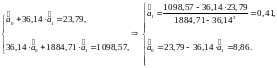
Отримано рівняння регресії 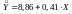. Зі збільшенням рівня механізації робіт на 1 % продуктивність праці збільшується на 0,41 т/год.

Відобразити поле кореляції та графік лінії регресії на одному графіку (рис. 1.1). Для цього слід розрахувати значення 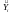(табл. 1.1).

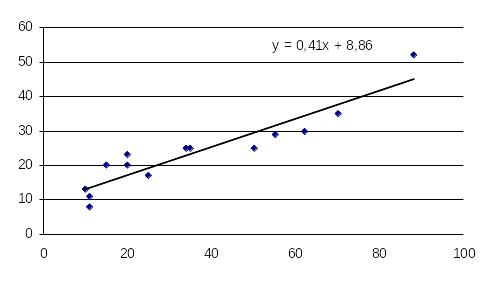
Рис. 1.1. Кореляційне поле

Тіснота лінійного зв’язку між залежною змінною Y та незалежною змінною Х оцінюється за допомогою коефіцієнта кореляції.

.

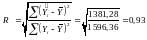Значення коефіцієнта кореляції R = 0,93 відображає досить тісний зв’язок між продуктивністю праці Y та рівнем механізації робіт Х.

Тоді коефіцієнт детермінації дорівнює 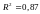. Це означає, що 87 % варіації продуктивності праці Y пояснюється варіацією фактора рівня механізації робіт Х.

Адекватність побудованої моделі оцінюється за допомогою F-критерію Фішера. Фактичне значення F-критерію:

.

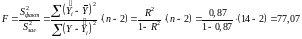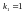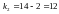Табличне значення критерію при п’ятивідсотковому рівні значимості і ступенях свободи і складає 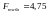. Оскільки 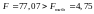, рівняння регресії вважається статистично значимим.

Для того, щоб мати загальне поняття про якість моделі із відносних відхилень по кожному спостереженню, визначається середня похибка апроксимації:

.

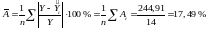Значення середньої похибки апроксимації перевищує допустимі межі 8–10 %. Однак враховуючи те, що в економічних дослідженнях припускається погрішність 10–20 %, можна зробити висновок про те, що модель досить точно описує залежності, які досліджуються, тобто можна сказати про високу якість побудованої моделі.

Стандартна похибка коефіцієнта регресії а₁ визначається за формулою:

,

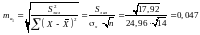де 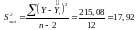– це залишкова дисперсія на один ступінь свободи.

Стандартна похибка параметра a₀ визначається за формулою:

.

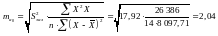Величина стандартної похибки разом з t-розподілом Ст’юдента при 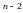ступенях свободи застосовується для перевірки істотності коефіцієнта регресії і для розрахунку його довірчого інтервалу.

Для перевірки значимості коефіцієнта регресії його величина порівнюється із стандартною похибкою. Визначається фактичне значення t-критерію Ст’юдента:

,

.

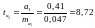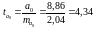Табличне значення критерію при рівні значимості α = 0,2 та числі ступенів свободи k = n – 2, .

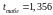Фактичні значення -статистики перевищують табличне значення: 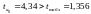, ,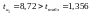 тому параметри а₀ і а₁ не випадково відрізняються від нуля і статистично значимі.

Необхідно розрахувати довірчі інтервали для параметрів регресії. Для цього визначити граничну похибку по кожному показнику.

,

.

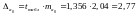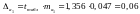Довірчі інтервали:

,

,

,

,

,

.

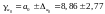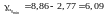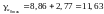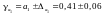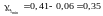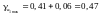Аналіз верхньої та нижньої межі довірчих інтервалів дозволяє зробити висновок про те, що з ймовірністю 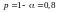параметри а₀ і а₁, знаходячись у вказаних межах, не приймають нульових значень, тобто вони статистично значимі та суттєво відмінні від нуля.

Отримані оцінки рівняння регресії дозволяють досить точно використовувати його для прогнозу. Якщо прогнозне значення рівня механізації складає 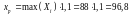%, то прогнозоване значення продуктивності праці складе: 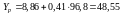т/год.

Похибка прогнозу становить:

.

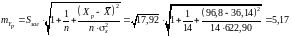Гранична похибка прогнозу, яка у 80 % випадків не буде перевищена і складе: .

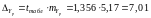Інтервальний прогноз значення Y_p:

.

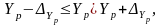
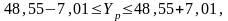
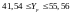Виконаний прогноз продуктивності праці є надійним з ймовірністю р = 0,8 і знаходиться в межах від 41,54 т/год. до 55,56 т/год.

Відобразимо прогнозне значення на полі кореляції:

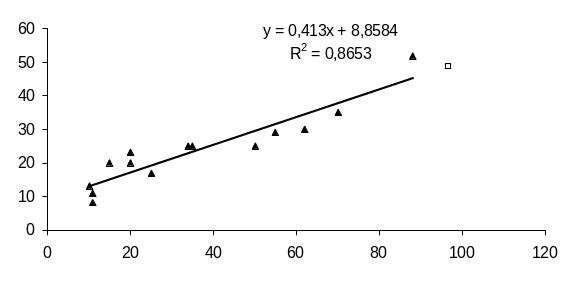
Рис. 1.2. Кореляційне поле з урахуванням прогнозного значення

Правильність розрахунків перевіримо за допомогою надбудови Анализ данных в MS Excel (рис. 1.3). Для цього потрібно виконати команду Сервис / Анализ данных. У діалоговому вікні, що з’явилося, слід вибрати пункт Регрессия, натиснути на ОК. На екрані з’явиться діалогове вікно Регрессия, в якому необхідно заповнити поля Входной интервал Х:, Входной интервал Y: та вказати додаткові параметри.

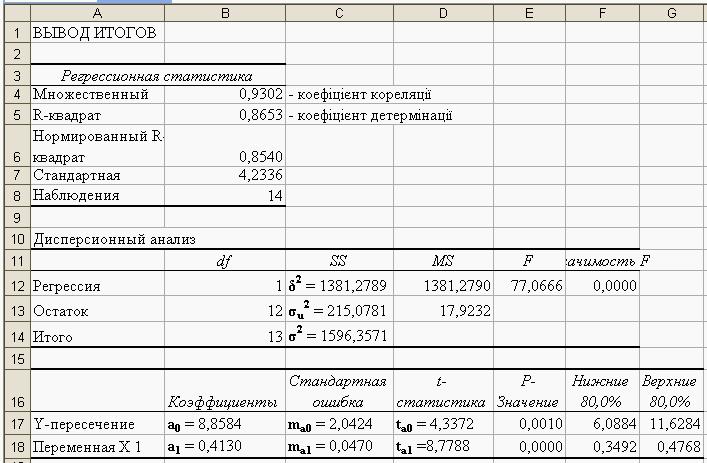
Рис. 1.3. Результат виконання інструменту Регрессия надбудови Анализ данных

Слід також використати пакет Statistica для перевірки результатів розрахунків. Для цього в меню Statistics (Статистика) обрати команду Multiple Regressions (Множественная регрессия). Відкриється стартова панель модуля, в якій проводиться вибір змінних за допомогою кнопки Variables (рис. 1.4).

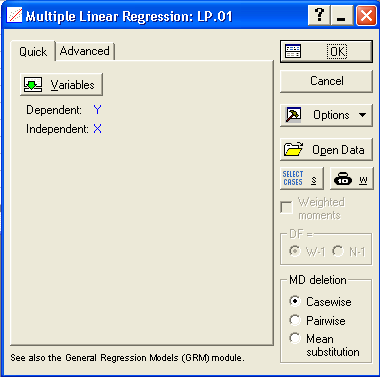
Рис. 1.4. Стартова панель модуля Multiple Linear Regression (Множественная регрессия)

Необхідно встановити прапорець на Advanced options (stepwise or ridge regression) і натиснути ОК. У вікні, що з’явиться, вказати стандартний метод побудови регресії та включити оцінку вільного члена регресії (Intercept).

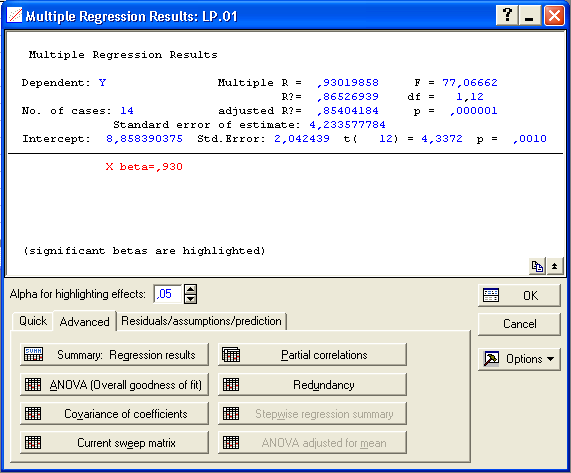
Рис. 1.5. Результати роботи модуля Multiple Regression (Множественная регрессия)

В інформаційній частині вікна наведені найбільш важливі параметри отриманої регресійної моделі:

Multiple R – коефіцієнт кореляції, який характеризує тісноту зв’язку між залежною та незалежною змінними. Може приймати значення від 0 до 1;

R² – коефіцієнт детермінації. Відображає частку варіації залежної змінної, що пояснюється за допомогою регресійного рівняння;

F – F-критерій використовується для перевірки значимості регресії. У даному випадку як нульова перевіряється гіпотеза про те, що між залежною і незалежною змінною немає лінійного зв’язку; df – число ступенів свободи для F-критерію; p – ймовірність нульової гіпотези для F-критерію;

Intercept – оцінка вільного члена рівняння;

t – t-критерій для оцінки вільного члена рівняння.

Натиснення на кнопку у вікні результатів (рис. 1.5) дозволяє отримати основні результати регресійної моделі (рис. 1.6), частина з яких уже описана: B – коефіцієнти рівняння регресії; St. Err. of B – стандартні похибки коефіцієнтів рівняння регресії; p-level – ймовірність нульової гіпотези для коефіцієнтів рівняння регресії.

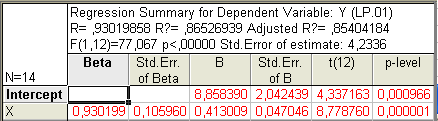
Рис. 1.6. Основні результати регресійної моделі

У результаті проведеного аналізу було отримано таке рівняння регресії:

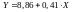, що підтверджує правильність побудови рівнянь регресії у попередніх розрахунках.

Це рівняння пояснює 87 % варіації продуктивності праці (R² = 0,87). Отримані результати свідчать про статистичну значимість коефіцієнтів регресії за t-критерієм.

Перевірка якості рівняння регресії здійснювалася за F-критерієм Фішера (F = 77,07). За статистичними таблицям Фішера–Снедекора з даними ступенями свободи df = 1, 12 гіпотезу Н₀ (лінійна залежність відсутня) можна прийняти з ймовірністю р = 0,000001. При рівні значимості α = 0,2 прийняти альтернативну гіпотезу – лінійна залежність значима.

Збудувати поле кореляції, на якому одночасно відобразити лінію регресії та рівняння регресії (рис. 1.7).

Для здійснення прогнозу скористатися кнопкою (розділ Residuals/assumptions/prediction). Задати значення для прогнозованого рівня механізації Х_р = 96,8. Провести як точковий, так і інтервальний прогноз (рис. 1.8).

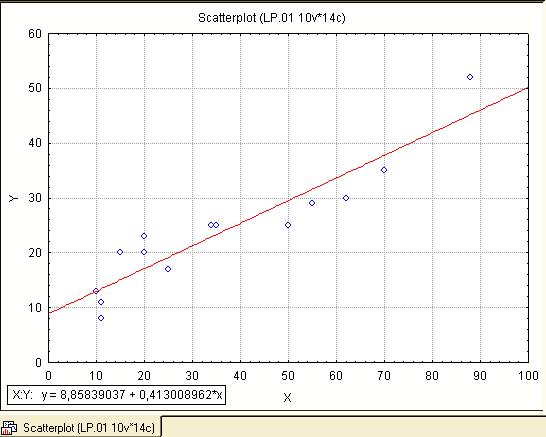
Рис. 1.7. Поле кореляції

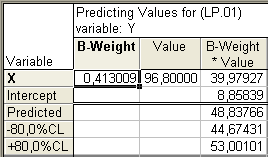
Рис. 1.8. Інтервальний та точковий прогноз

Отримані результати такі: Y_p = 48,83 – точковий прогноз, 80 %-ний довірчий інтервал [44,67; 53,00].