Статистическая структура двоичной функции.

41. Понятие статистического аналога двоичной функции.

Будем считать, что значения переменных двоичной функции f(,..,)являются независимыми случайными величинами с распределением

.

Тогда для любого двоичного набора

и

, где .

Двоичную функцию называютстатистическим аналогомфункцииf(,..,), если . Заметим, что если для некоторой функцииg(x) , то стaтистическим аналогом функцииf(x)будет функция.

Так как для линейных систем уравнений имеются достаточно эффективные методы их решения, то при анализе спецаппаратуры зачастую стремятся использовать линейные статистические аналоги.

42. Понятие статистической структуры двоичной функции.

4) Статистическая структура двоичной функции.

Определим для функции f(x)и линейной функции параметр исходя из равенства.

Определение. Набор чисел называетсястатистической структуройдвоичной функцииf(x).

Набор чисел показывает насколько отличаются от ½ вероятности совпадения значений функциисо значениями линейных функций(a,x), .

Выведем формулу для вычисления коэффициентов статистической структуры. Имеем

=.

Отсюда ,.

43. Доказательство связей значений коэффициентов Фурье двоичной функции со значениями ее статистической структуры.

5) Связь коэффициентов Фурье двоичной функции со значениями её статистической структуры.

По определению коэффициетов Фурье двоичной функции приа=0имеем.

При .

С другой стороны

Сравнивая окончательные выражения для правых частей равенств получаем прии.

Используя эти равенства и представление двоичной функции в виде ряда Фурье получаем представление двоичной функции через коэффициенты ее статистической структуры:

Так как коэффициенты Фурье однозначно определяют двоичную функцию, то и статистическая структура однозначно определяет двоичную функцию.

44. Методы вычисления статистической структуры двоичной функции.

6) Методы вычисления статистической структуры двоичной функции.

Способ вычисления коэффициентов статистической структуры двоичной функции, основанный на формуле ,является достаточно трудоемким. Для каждого коэффициента(их всего) необходимо найти вес функции т.е. сначала провести сложение функций, а затем подсчитать сумму слагаемых). Поэтому трудоемкость

этого способа оценивается величиной слагаемых операций сложения.

Более эффективный способ основан на использовании связей статиистической структуры функции со статистическими структурами ее подфункций (такой способ использует, так называемое, быстрое преобразование Фурье). Имеем

.

Для удобства полагаем

.

При введенных обозначениях имеет место

45. Доказательство теоремы о связи статистической структуры двоичной функции состатистическими структурами ее подфункций

Утверждение. (О связи статистической структуры функции со статистическими структурами ее подфункций). Коэффициенты статистических структур двоичной функции и ее подфункциийисвязаны соотношениями;.

Доказательство.

случай , т.е.. В этом случае имеем

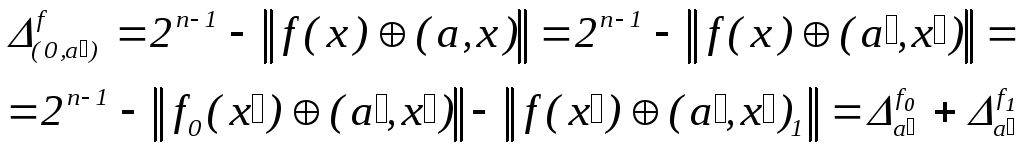
случай , т.е.. Имеем

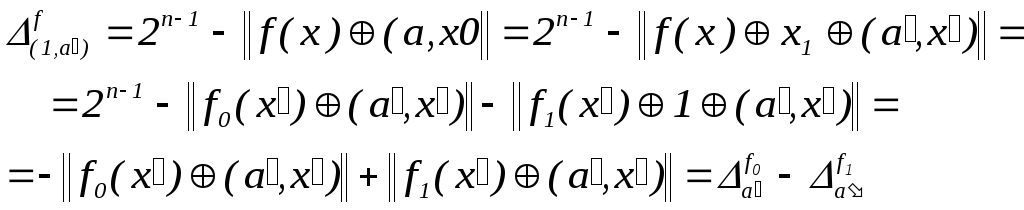
Утверждение полностью доказано.

Данное утверждение позволяет вычислять статистическую структуру функции исходя из статистических структур подфункций=и=по следующему правилу. Если

,

то статистическая структура функции равна

Для вычисления статистических структур функций ив свою очередь, используют разложения

и т.д.

Продолжая этот процесс доходят до функций от одной переменной вида

Статистические структуры таких функций легко считаются, их значения приведены в таблице

0	1	0
	0	1
	0	-1
1	-1	0

Изложенный способ определения коэффициентов статистической структуры двоичной функции от nпеременных выполняется заnшагов, в каждом из кото- рых приходится вычислятьзначений коэффициентов статистических структур. Поэтому оценка трудоёмкости данного способа имеет видв операциях сложения и вычитания.