Конечные поля.

Простейшие свойства полей: Р – поле – это коммутативное К с е, в котором каждый ненулевой элемент обратим. .

Свойства:

1. (P,+) – коммутативная группа G

   1. 

   2. 

   3. a+b=b+a

   4. 

   5. 

2. 

   2. 

3. т.к. К – коммутативно значит ab=ba

4. 

Пример1: рациональные действия, комплексные числа – поля.

Пример2: GF(2) – поле Галуа (конечное поле)

- такое множество элементов {0,e} – поле.

Пример3: Zp (если р – простое) – поле.

Пример4: - множество таких чисел образует поле. Оно больше Q, но меньше поля R.

Опр: Характеристика поля Р – минимальное натуральное число р. 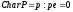. Если такого р не существует, по определению полагают р=0.

Пример5: GF(2), т.к. e+e=0, т.е. 2e=0, a .

Пример6: R .

Пусть Р – конечное поле. Построим последовательность: e,2e,3e,…,ne, т.к. в поле конечное число элементов значит где-то есть повторения: (Пусть k>j)

Пусть ke=je; (k-j)e=0. (k-j) – какое-то натуральное число, пусть не min, т.е. это верхняя граница значит есть min. Значит если Р – конечно, то , т.е. конечное поле имеет конечную характеристику.

Замечание: Обратное не верно, существуют бесконечные поля, имеющие конечную характеристику.

Утв1: Пусть Р – конечное поле - простое число.

Док-во: от противного. Пусть

1. 

2. 

Лемма: “В поле нет делителей нуля”.

Док-во: Пусть , а т.к. b=0 – противоречит с выбором b. Значит в поле отсутствует делитель нуля

2) – противоречит тому, что Р – поле, следовательно наше предположение о том, что Р=n₁n₂ – ошибочно, значит Р – простое число.

Опр.: Пусть Р – поле следовательно множество Q P – подполе Р, если QP и Q – поле.

Пример: Q < R < C

Опр.: Поле называется простым, если оно не содержит собственных подполей, т.е. если Q<P значит Q=P(более простых полей, чем Р в нем нет).

Теорема: В каждом поле существует, причем единственное, простое подполе.

Доказательство:

1) Пусть char P=0, eP

Пусть Q<P. Тогда рассмотрим множество Q*=Q\0 – множество ненулевых элементов подполя Q – это мультипликативная группа, а Q*P*. Тогда Q*<P*, а е – подгруппа Q* совпадает с е в Р*, т.к. ab^-1Q*; пусть aQ*, b=a и е=аа^-1Q*, т.е. еQ* - единица принадлежит подполюQэ{0,e}, а т.к. Qэe , то 2e, 3e, …Q – в силу замкнутости по сложению. а т.к. (Q,+) – группа, то -е, -2е, -3е, … Q n\0, (ne)^-1Q – существование обратного по умножению m, n\0, (me)(ne)^-1=eQ – в силу замкнутости по умножению

Вывод: если char P=0, то {eQP, m, n\0}=P₀, т.е. если Q – подполе, то P₀Q, для Q<P.

Теперь покажем, что Р₀ – поле:

1. = операции сложения и умножения замкнуты

2. ассоциативность, коммутативность следуют из ассоциативности, коммутативности Р

3. дистрибутивность

4. обратное по сложению

5. обратное по умножению

Р₀ – поле.

Покажем, что Р₀ – простое поле: Пусть существует Q'<P₀, а по доказанному P₀<Q' следовательно Q'=P₀ ч.т.д.

Замечание: из доказательства следует, что простое подполе поля с характеристикой равной нулю изоморфно полю рациональных чисел, т.к. {QP, m, n\0}=P₀ (е – опускаем).

2) Пусть char P=Р

а) т.к. Q<P значит eQ (было доказано выше), следовательно е,2е,…,(р-1)е, ре=0, следовательно {0, e, 2e, …, (p-1)e}=P₀

Рассмотрим Z_p: пусть : P₀Z_p

(a,e)=[a]_p – взаимно однозначное отображение

(aebe)=(ae) (be), где

следовательно P₀Z_p (т.е. изоморфны), значит т.к. Р₀ - поле, т.к. Z_p – поле.

б) Р₀ – простое, т.к. Q'P₀ и P₀Q' следовательно Q'=P₀ ч.т.д.

Теорема: Пусть P – конечное поле, тогда существует Р : ord=-1; (ord - по умножению в мультипликативной группе Р*).