§ 5. Приложение

1. Классические и квантовые вероятности.

а) Классические вероятности.

Здесь мы дадим некоторую трактовку классических вероятностей, перекидывая "мостик" к квантовым вероятностям.

Обозначим через

дискретную вероятностную схему.

Пусть (i)=_i-случайная величина, заданная на (1, 2, ... , m).

Мы будем интересоваться вероятностью того, что случайная величина  примет значение _i из некоторого подмножества

(i₁, i₂,…, i_k)=()

Введем в рассмотрение вектор-столбец =, диагональную матрицу (оператор)

.

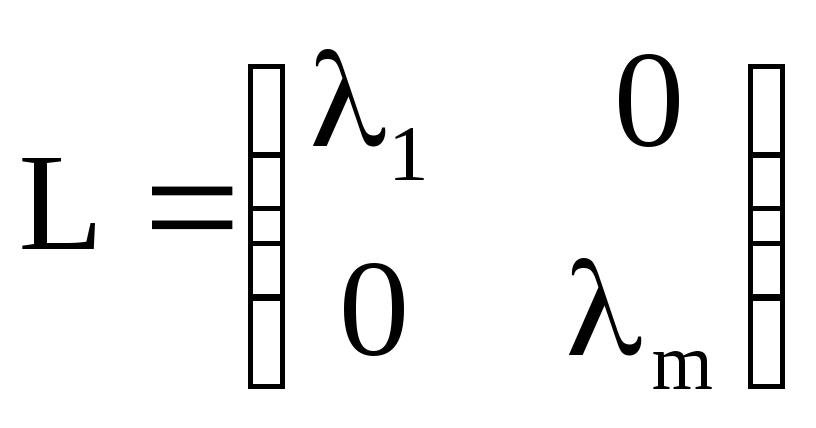Собственные вектора оператора L есть единичные вектора =с собственными значениями.

Введем в рассмотрение операторы (c одной единицей на диагонали) вида

(i)= ,-вектор-строка.

Тогда нетрудно видеть, что вероятность

P(=_i)=(i)==,

где .

Пусть

={i₁, i₂, ... , i_k}- подмножество индексов {1, 2, ... , m},

()=- проектор на соответствующее подпространство.

Тогда Р((i₁, i₂,…, i_k))=.

б) Квантовые вероятности [11].

В гильбертовом векторном пространстве H размерности m над полем комплексных чисел рассмотрим вектор ,и назовем его состоянием квантовой системы.

Пусть B - положительно определенный эрмитов оператор, - его собственные вектора с собственными значениями, множество(i₁, i₂,…, i_k)=()

Введем в рассмотрение проекционные операторы (i)= .

Пусть ={i₁, i₂, ... , i_k}- подмножество индексов {1, 2, ... , m},

()=- проектор на соответствующее подпространство.

Введем в рассмотрение вероятности

Р((i₁, i₂,…, i_k)) = .

Совокупность операторов (), получающихся при отображении (), называется вероятностно-операторной мерой.

Оператор называется оператором плотности состояния.

Будем говорить, что прибор, применяющий такую вероятностно-операторную меру к квантовому состоянию , измеряет оператор B.

в) Поляризованные фотоны как квантовые состояния.

Рассматривается гильбертово пространство H размерности 2. Здесь мы имеем m=2 и, соответственно, 2 исхода с номерами 1 и 2.

Любое состояние в таком гильбертовом пространстве может быть представлено в виде вектора =(cos, sin), гдеотвечает углу поляризации фотона.

Рассмотрим вектор = (cos, sin) и определим оператор (проектор) . Этот оператор имеет собственный векторс собственным значением 1 и любой вектор, ортогональный к вектору, является собственным с собственным значением 0. Тогда

Р(1) = =

==

=cos²cos² + 2 coscos sinsin + sin²sin² = cos²(-).

Аналогично

Р(0) = sin²(-).

Так определенное квантовое измерение соответствует регистрации поляризованного фотона в прямом и перпендикулярном луче двоякопреломляющей призмы с углом оптической оси .

2. Вероятность ошибки при атаке на квантовый канал.

а) Атака с использованием алгоритма приема поляризованных фотонов Боба.

Здесь мы предположим, что Ева применяет для определения поляризации фотона тот же самый алгоритм, что и Боб, каждый раз производя измерения и отправляя к Бобу новый фотон, поляризуя его в соответствии с результатами измерений. Очевидно, что после согласования базисов Алисой и Бобом и вычеркивании номеров тактов с "пустыми" импульсами, на оставшейся части битовой последовательности вероятность совпадения базисов у Алисы (Боба) и Евы будет равна ½. Тогда, на этой части битовой последовательности, где совпали базисы у всех 3-х участников, значения бит Алисы, Боба и Евы будут совпадать.

Там, где базисы Евы не совпали с базисами Алисы и Боба, Ева принимает значения бит случайно, равновероятно и независимо от битовой строки Алисы. В этом случае можно считать, что она отправляет к Бобу случайную и равновероятную последовательность {} поляризованных фотонов, выбирая конкретную поляризацию из множества {0°, 45°, 90°, 135°}.

Тогда, на этой части последовательности, вероятность совпадения бит у Алисы и Боба будет равна:

P(/несовп. баз)= P(,_i=1)+ P(,_i=2)=(P(_i=1)+P(_i=2)).

По формуле полной вероятности

P(_i=1)=.

Ясно, что

P(_i=1/=0°,=0°)=1, P(_i=1/=90°,=0°)=0,

P(_i=1/=45°,=45°)=1, P(_i=1/=135°,=45°)=0,

а во всех остальных случаях

P(_i=1/,)=1/2.

Тогда

P(_i=1)==.

из соображений симметрии также можно показать, что

P(_i=2)=.

Следовательно,

P(/несовп. баз)=.

Вероятность ошибки в полной битовой строке Алисы и Боба составит величину

P()=1-P()=1-(P(/совп. баз)+P(/несовп. баз))=,

т.к. P(/совп. баз)=1.

Аналогично можно показать, что

P()=

и в том случае, когда Ева производит измерения только в прямоугольном или только в диагональном базисе.

б) Атака с использованием промежуточного базиса.

Здесь мы предполагаем, что при измерениях Ева устанавливает на некоторый постоянный угол  оптическую ось своей двоякопреломляющей призмы и принимает следующие решения относительно значений битовой строки Алисы:

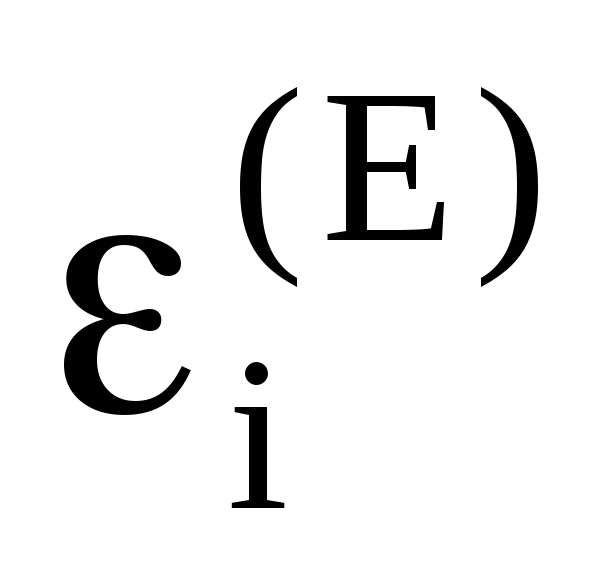• =0, если регистрация наблюдения происходит в прямом луче,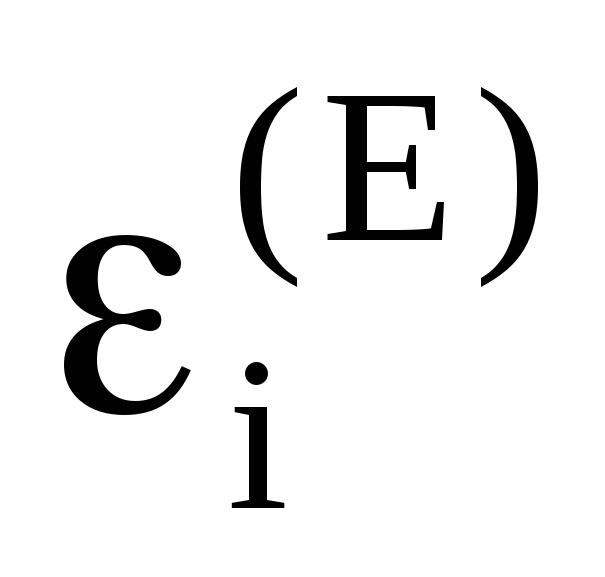

• =1, если регистрация наблюдения происходит в ортогональном луче, 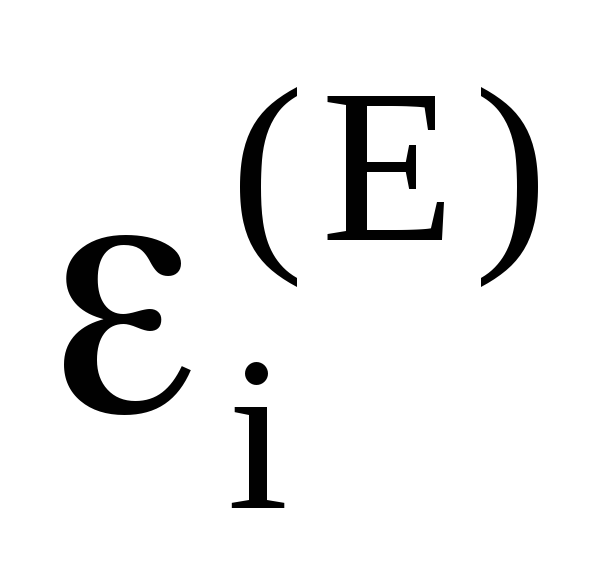-оценка неизвестного бита Алисы .

Как было сказано выше, нулевой (единичный) бит ключа кодируется либо одним состоянием поляризации либо другим в зависимости от выбранного базиса. Поэтому, если. например, Ева принимает решение о том, что был послан нулевой бит ключа ( =0), то у нее есть две возможности для кодирования и пересылке к Бобу: 0⁰ или 45⁰ (90⁰ или 135⁰ для единичного бита).

Мы будем полагать, что Ева всегда принимаемый нулевой бит ключа кодирует состоянием 0⁰, а единичный бит - состоянием 90⁰. Можно показать, что никакие рандомизированные процедуры, состоящие в случайном выборе состояний поляризации для пересылки к Бобу не улучшают стратегию подслушивания.

Наблюдения Евы состоят из двух исходов:

• "" – регистрация фотона в прямом луче , тогда =0,

• "" – регистрация фотона в ортогональном луче, тогда 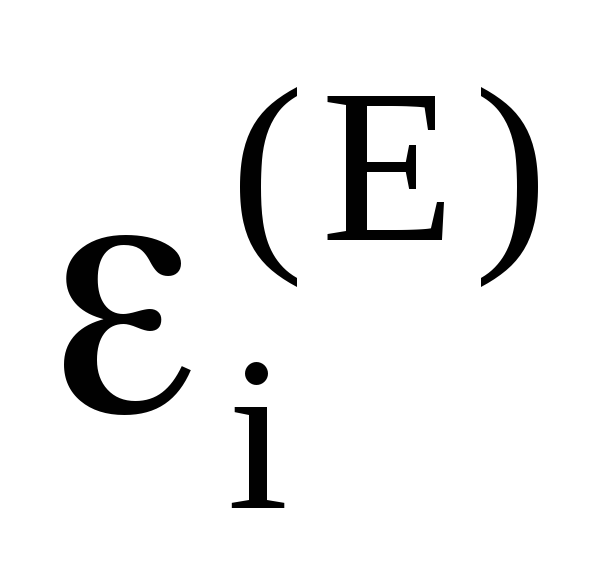=1.

Нетрудно показать, что условные распределения вероятностей имеют следующий вид:

,

.

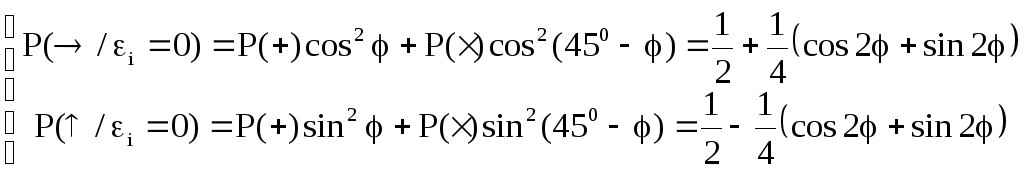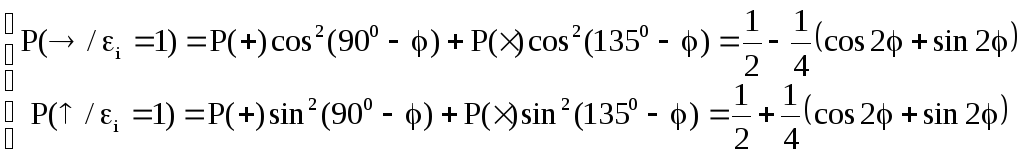Отсюда легко видеть, что условная вероятность правильной классификации

==.

Далее, вероятность совпадения бит у Алисы и Боба равна

=.

=.

+

+=

=.

+

+.

Следовательно,

=(+)=.

Аналогично можно показать, что

=.

Таким образом, вероятность совпадения бит у Алисы и Боба равна

=

и вероятность ошибки

.

Минимальное значение вероятности ошибки достигается при значении ₀=22.5⁰ и равно

.