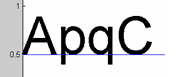Преобразование формулы в рисунок (объект Image)

На сайте http://www.mathworks.com/matlabcentral/ в File Exchange > Graphics > Specialized Plot and Graph Types можно скачать функцию teximage, которая по заданной строке с формулой в формате LaTeX создает рисунок, т.е. объект Image. Это оказывается полезным, при размещении формул не на осях, а на других графических объектах, например, кнопках.

Часть 2 Базовые графические объекты.

Базовые (Core) графические объекты занимают нижний уровень в иерархии графических объектов MATLAB, предком базовых графических объектов являются оси. Следовательно, их вывод возможен только при наличии осей, которые при желании можно сделать невидимыми и, кроме того, совпадающими по размеру с графическим окном. Тогда базовые объекты можно размещать в произвольном месте области графического окна. Всего в MATLAB существует семь базовых графических объектов:

• Рисунок (Image). Создается функцией image, в списке ее входных аргументов надо указать массив, содержащий информацию о цвете каждого пикселя в формате RGB (трехмерный массив) или индексированный цвет (двумерный массив). Для чтения этой информации из графического файла служит функция imread, которая понимает основные графические форматы: bmp, gif, jpeg, pcx, tiff и др.

• Источник света (Light). Создается функцией light и служит для освещения поверхности (Surface) и полигонального объекта (Patch). На одних осях может быть расположено несколько источников света, каждый со своими свойствами: цвет света, тип лучей. Лучи могут быть параллельные, т.е. идущие от бесконечно удаленного источника, или лучи, исходящие из точечного источника, расположенного в определенной точке пространства.

• Линия (Line). Ломаная линия создается функцией line и задается координатами вершин. Возможно изменять стиль, цвет и толщину линии, размещать различные маркеры в вершинах и выбирать их размер, цвет границы и внутренности.

• Полигональный объект (Patch). Создается функцией patch. Служит для создания плоских и трехмерных объектов, в том числе и достаточно сложной формы. Полигональный объект задается либо координатами вершин каждой грани, либо координатами всех вершин и тем, какие грани они образуют. Возможны различные способы закраски граней и ребер полигонального объекта: как постоянным цветом, так и цветами, меняющимися от вершины к вершине, а также указание прозрачности граней и ребер и свойств, отвечающих за освещение полигонального объекта

• Прямоугольник (Rectangle). Создается функцией rectangle, которая позволяет указать величину скругления углов. Так что можно рисовать не только прямоугольник или квадрат, но и эллипс и круг. Возможно изменять цвет границы и внутренности, а так же стиль линии границы.

• Поверхность (Surface). Создается функцией surface. Поверхность задается на прямоугольной сетке значениями в каждом ее узле. Обычно, для создания прямоугольной сетки применяется функция meshgrid. Возможно изменение цвета ячеек и их границ, способов их закраски, прозрачности ячеек и границ, свойств линий границ ячеек, указание свойств, отвечающих за освещение поверхности светом, а также размещение маркеров заданного вида, размера и цвета в вершинах ячеек.

• Текстовый объект (Text). Создается функцией text. Текст может быть отформатирован различными шрифтами и начертанием, цветом, заключен в рамку (свойства линий рамки и цвет ее внутренности можно изменять), повернут на заданный угол. Для набора математических формул доступны возможности TeX и LaTeX.

В справочной системе MATLAB информация о базовых объектах доступна в нескольких разделах:

• Справочник свойств графических объектов MATLAB: Handles Graphics Property Browser (в правом окне далее надо перейти по гиперссылке Axes, далее в дереве по ссылке Core Objects).

• MATLAB: Graphics: Handle Graphics Objects: Core Objects.

• Работа с графическими изображениями (объектами Image) описана в разделе MATLAB: Graphics: Displaying Bit-Mapped Images.

• Моделирование сложных объектов при помощи полигональных объектов рассмотрено в разделе MATLAB: 3-D Visualization: Creating 3-D Models with Patches.

• Техника освещения объектов разбирается в разделе MATLAB: 3-D Visualization: Lighting as a Visualization Tool.

• Свойства графических объектов, отвечающие за их прозрачность и их использование см. в разделе MATLAB: 3-D Visualization: Transparency.

• Кроме того, для быстрого перехода к свойствам объектов можно посмотреть справку по низкоуровневой функции, которая создает данный объект: image, text, line, rectangle, surface, patch, light, например:

>> doc text

(для отображения окна браузера справочной системы с информацией о функции text и текстовом объекте), или

>> help text

(для вывода краткой информации о функции text в командное окно, выводятся также гиперссылки для перехода к описанию родственных функций).

Текстовый объект, вывод текста и математических формул в графическое окно.

В этом разделе описана работа с текстовыми объектами, которые создаются функцией текст. Мы рассмотрим задание положения текстового объекта, его вида, разберем свойства текстовых объектов, отвечающие за форматирование шрифта и других настроек текстовых объектов, включая поворот, рамку вокруг текста и вывод многострочного текста. Отдельные подразделы посвящены выводу многострочного текста и написанию математических формул.

Размещение текстового объекта, определение его размеров и положения.

Начнем с простого примера, в котором график функции следует снабдить текстовой информацией так, как на приведенном ниже рисунке.

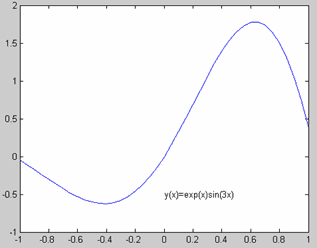
Для получения такого графика достаточно выполнить следующие команды:

>> x = -1:0.05:1;

>> y = exp(x).*sin(3*x);

>> plot(x, y)

и добавить текстовый объект при помощи функции text. Первыми ее входными аргументами являются координаты объекта, а сам текст задается строкой:

>> hT = text(0, -0.5, 'y(x)=exp(x)sin(3x)')

Функция text возвращает указатель на созданный текстовый объект, который в данном случае записан в переменную hT. Он может понадобиться для дальнейшего изменения свойств текстового объекта, например размера шрифта. По умолчанию, размер шрифта 10 пт, что написано в справочной системе MATLAB в разделе с информацией о текстовых объектах, до которого проще всего добраться при помощи команды

>> doc text

(см. таблицу внизу страницы этого раздела справочной системы). За размер шрифта отвечает свойство FontSize. Напомним, что текущее значение какого-либа свойства графического объекта всегда можно узнать при помощи функции get:

>> get(hT, 'FontSize')

ans =

10

Действительно, размер 10 и именно пунктов, поскольку в MATLAB пункты выбраны по умолчанию в качестве единиц для задания размера шрифта. Выбор единиц измерения размера шрифта определяется значением свойства FontUnits текстового объекта, которое по умолчанию есть 'points' (т.е. пункты, 1пт = 1/72 дюйма). Возможно отказаться от пунктов и выбрать другие значения свойства FontUnits, ими могут быть:

• 'inches' (дюймы);

• 'centimeters' (сантиметры);

• 'pixels' (пиксели);

• 'normalized' (нормализованные).

Выбор нормализованных единиц удобен, если размер шрифта должен определяться размером осей (1 нормализованная единица равна высоте осей), скажем, требуется разместить текстовую надпись высотой в половину высоты оси ординат:

>> figure

>> axes

>> hT1 = text(0, 0.5, 'ABC')

>> set(hT1, 'FontUnits', 'normalized', 'FontSize', 0.5)

Кроме того, выбор нормализованных единиц приводит к автоматическому изменению размеров шрифта при изменении размеров осей.

В этом примере мы сначала создали графическое окно и оси при помощи функций figure и axes, соответственно. Обратите внимание, что по умолчанию функция axes создает оси, у которых пределы оси абсцисс и оси ординат есть [0, 1]. При выводе текстового объекта функцией text мы указали координаты: 0 по оси абсцисс и 0.5 по оси ординат. Сейчас абсцисса левого нижнего угла текстового объекта равна нулю, а середина текстового объекта по вертикали имеет ординату 0.5. Так происходит потому, что два свойства текстового объекта: HorizontalAlignment и VerticalAlignment, отвечающие за выравнивание текста соответственно по горизонтали и вертикали, по умолчанию имеют следующие значения:

HorizontalAlignment = 'left' и VerticalAlignment = 'middle'.

Свойство HorizontalAlignment может принимать значения 'left' (по умолчанию), 'center' и 'right', а VerticalAlignment - 'top', 'cap', 'middle', 'baseline', 'bottom'. Смысл значений свойства HorizontalAlignment вполне очевиден. Значения 'cap', 'middle' и 'baseline' означают вертикальное выравнивание по заглавным буквам, середине и нижней линии текста, соответственно. Поместим текст "ApqC" размера 70пт в точку с координатами (0, 0.5) и для наглядности нарисуем линию, параллельную горизонтальной оси, которая проходит через y = 0.5:

>> figure

>> axes

>> hT2 = text(0, 0.5, 'ApqC')

>> set(hT2, 'FontSize', 70)

>> line([0 1], [0.5 0.5])

Теперь, изменяя значение свойства VerticalAlignment, можно понаблюдать за поведением текста, см. рисунки:

>> set(hT2, 'VerticalAlignment', 'baseline')
>> set(hT2, 'VerticalAlignment', 'cap')
>> set(hT2, 'VerticalAlignment', 'middle') (как по умолчанию)

Значения 'top' и 'bottom' свойства VerticalAlignment означают выравнивание некоторого прямоугольника, в который заключен текст (): 'top' - верхняя сторона прямоугольника имеет заданную координату (в нашем примере 0.5), 'bottom' - нижняя сторона прямоугольника имеет заданную координату (также 0.5 в нашем примере). Координаты этого прямоугольника определяются значением свойства Extent текстового объекта. Это свойство доступно только для чтения, его нельзя изменять и его значением является вектор из четырех элементов [left, bottom, width, height], где left и bottom - координаты левого нижнего угла прямоугольника, а width и height, соответственно, ширина и высота. По умолчанию, эти величины заданы в системе координат осей. Так происходит потому, что свойство Units (не путать с FontUnits) по умолчанию имеет значение 'data'. Другими возможными значениями свойства Units являются 'pixels' (пиксели), 'inches' (дюймы), 'centimeters' (сантиметры), 'points' (пункты) или нормализованные единицы (считается, что левый нижний угол осей имеет координаты (0, 0), а правый верхний - (1, 1)). Если значение свойства Units отлично от 'data', т.е. мы работаем не в системе координат осей, то меняется и смысл элементов вектора [left, bottom, width, height], который является значением свойства Extent. Именно, элементы left и bottom теперь равны расстоянию от нижнего левого угла осей по горизонтали и вертикали, соответственно, а width и height - ширина и высота прямоугольника, ограничивающего текстовый объект. Разумеется, left, bottom, width и height заданы в тех единицах измерения, которые выбраны при помощи свойства Units текстового объекта.