Третья навигационная задача решается в навигационной аппаратуре при известных текущих координатах для определения координат разведанных целей. Дальномером определяют Д_ц дальность до цели и угол _виз визирования на нее. Принцип решения задачи показан на Рис.2.34. ,а функционально-логическая схема на Рис.2.35.

X_ц= _ц Д_ц cos _ц;

_ц= _ц= Д_ц sin _ц; (2.48.)

где

_ц= + _вн3, при + _вн3 <(60-00)

_ц= + _вн3-(60-00), при + _вн3 >(60-00)

Наиболее типичной аппаратурой, решающей 1,2 и 3-ю навигационные задачи, является танковая навигационной аппаратура типа ТНА. Ее общая схема и приборный состав ясны из Рис.2.36.

Комплект одометрической навигационной аппаратуры такого типа включает в свой состав все необходимые устройства для решения трех навигационных задач . При решении первой навигационной задачи текущие значения скорости V(t) пройденного ОН пути и дирекционного угла (t) определяются путевой ПС и курсовой КС системами. В начальной точке О маршрута необходимо введение исходных координат X_исх и Y_исх и дирекционного угла _исх. Их введение может производиться автоматически с использованием приемно-индикаторной аппаратуры спутниковых радионавигационных систем. Гироскопический курсоуказатель, являясь трех степенным гироскопом направления, измеряет приращение 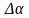дирекционного угла _исх . Суммирование ( _исх+ ) происходит с помощью следящей системы СС и на ее выходе происходит разворот синусно-косинусного трансформатора СКП на угол _исх+ . Выходы СКП, пропорциональные cos и sin , поступают на умножители УМН, в которые подаются также сигналы V путевой скорости ОН и коэффициента К корректуры пути. Таким образом, один умножитель вырабатывает сигналы V_к cos , пропорциональные приращению координаты X, а второй – приращению координаты Y. После сложения исходных координат X_исх ,Y_исх с их приращениями и значений текущих координат X и Y поступают потребителю и на планшет П, где они индицируются, и вычерчивается пройденный маршрут на карте. Коэффициент К корректуры пути устанавливается в зависимости от дорожных условий и его значение выбирается из таблиц, составленных по результатам многочисленных испытаний ОНС данного типа в различных дорожных условиях.

Таким образом, в счетно-решающем приборе СРП1 первой навигационной задачи и счетчиках С_чX и С_чY происходит вычисление текущих координат по алгоритмам (2.46).

Путевая система ПС включает в свой состав датчик скорости ДС и интегратор И. Частота следования импульсов ДС пропорциональна текущей скорости V. Так как цена одного импульса соответствует конечному пройденному расстоянию (например, 1 импульс – 1 метр), то для получения величины пройденного пути S достаточно в интеграторе И производить их суммирование.

При решении второй навигационной задачи о выходе ОН в заданный пункт назначения на начальной точке маршрута данные о ее координатах X_исх, Y_исх и известных координатах X_пн и Y_пн пункта назначения вводятся в счетно-решающий прибор СРП2 второй навигационной задачи, который по алгоритмам (2.47) вычисляет исходное расстояние S_{пн исх} до пункта назначения и исходный дирекционный угол _{пн исх} до пункта назначения. В процессе движения СРП2, получая дополнительно информацию о приращениях кординат и , вычисляет текущее значение S_пн и , а при необходимости и текущее разности координат _пн , _пн до пункта назначения.

При решении третьей навигационной задачи об определении неизвестных координат X_ц, Y_ц пункта назначения (или цели) на начальной точке маршрута в счетно-решающий прибор СРП3 третьей навигационной задачи вводят расстояние до цели (дальность Д_ц) и угол _виз визирования на нее. Вычисление координат X_ц, Y_ц цели проводится в СРП3 и сумматорах по алгоритмам(2.48). Индикация результатов определения навигационной информации в объеме второй и третьей навигационных задач (S_пн, _пн, _пн, _пн, X_ц, Y_ц) может проводиться при необходимости как на шкалах приборов ОНС, так и у потребителя.

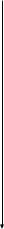X

Ц

X_ц- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -- -

_ц

_ц Д_ц

_виз

X - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Y

Y _ц Y_ц

Рис.2.34. Схема и принцип решения третьей навигационной задачи.

_{ц виз} при _виз < 60 – 00;

_{ц виз}-(60 - 00) при _виз > 60 – 00;

Д_ц – дальность до цели;

_виз – угол визирования на цель;

Х_ц, _ц - координаты цели;

Х, - текущие координаты ОН;

_ц, _ц – приращение координат до цели;

_ц – угол направления на цель.

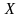
_{виз ц ц}

_ц

СПР_ц

Д_{ц ц}

_ц

Рис.2.35. Функционально-логическая схема решения третьей задачи.

Ввод исходных данных S_пн, Д_ц для решения второй и третьей задач может проводиться автоматически дистанционно с центрального поста управления в режиме целеуказания.

Погрешности и определения координат могут быть определены из системы уравнений (2.46) введением ошибок установки начальных данных _исх, _исх, _исх; определения путевой скорости V и дирекционного угла ; ошибок _срп, _срп счетно-решающего прибора

_{t t}

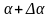_исх+ (V+ V) cos( ) dt - V cos dt + _срп;

^{0 0}

_{t t} (2.49.)

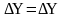_исх+ (V+ V) sin( ) dt - V sin dt + _срп;

^{0 0}

где принято =0.

_изм+ _гку – ошибка курсовой системы (КС);

_изм= _исх+ _сс;

_исх – ошибка установки начального угла _исх;

_сс – ошибка курсовой следящей системы;

_гку = _гку t – угол ухода гирокурсоуказателя КС.

_гку - скорость ухода гирокурсоуказателя КС.

Упрощая выражение (2.49) и учитывая малость углов , пренебрегая величинами высшего порядка малости, получим:

_{t t}

_исх+ V cos dt - V sin dt + _срп;

^{0 0} (2.50.)

_{t t}

_исх+ V sin dt - V cos dt + _срп.

^{0 0}

Введя обозначения

_{t t}

_V = V cos dt; _V = V sin dt;

^{0 0}

_{t t}

= V sin dt; = V cos dt;

1. ⁰

получаем

_исх+ _V + + _срп;

_исх+ _V + + _срп. (2.51.)

Переходя к относительным ошибкам с учетом коэффициента маневра К_м можно получить:

• относительные ошибки _исх, _исх из-за ошибок установки исходных координат

_исх= _исх /S; _исх= _исх /S; (2.52.)

• относительные ошибки _V и _V из-за ошибок определения путевой системой скорости

_t

_V = _V /К_м S К_м S) V cos _ср dt=(cos _ср/К_м) S;

_{0t (2.53)}

_V = _V /К_м S К_м S) V sin _ср dt=(sin _ср/К_м) S;

₀

_{где Км=S/S0 – коэффициент маневра;}

_{S – пройденный путь, S0 – кратчайшее расстояние между начальной и конечной точкой маршрута длиной S;}

_{ср - средний дирекционный угол данного маршрута;}

_{-относительные ошибки} и _{из-за ошибки курсовой системы:}

_{t t}

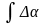= /К_м S К_м S) V sin _ср dt=(sin _ср/К_м) _изм+(sin _ср/К_м t) _гку dt; ^{0 0}

_{t t (2.54)}

= /К_м S К_м S) V cos _срdt=(cos _ср/К_м) _изм+(cos _ср/К_м t) _гку dt; ^{0 0}

• относительная ошибка S определения пути

S = S/S;

• относительные ошибки _срп, _срп счетно-решающего прибора

_срп= _срп/S; _срп= _срп/S; _срп= _срп=1/2 Z; (2.56.)

где Z - число уровней квантования в СКП единицы (значения 1=sin90 cos0 .

Окончательно можно записать

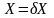_исх+ _V + _срп;

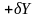_{исх V} + _срп;

где

= _гку+ _изм; = _гку+ _изм;

_изм=sin _ср/К_{м изм}; _изм=con _ср/К_{м изм};

_{t t}

_гку=(sin _ср/К_м t) _гку dt; _гку=(cos _ср/К_м t) _гку dt;

^{0 0}

Дисперсии погрешностей

D =D _исх+D _изм+D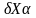 _гку+D _срп;

(2.58)

D =D _исх+D _изм+D _гку+D _срп;

С учетом равенства нулю математических ожиданий ошибок в результате оптимальной настройки ОНС среднеквадратические погрешности можно определить по следующим зависимостям G² =G² _исх+(cos² _ср/К²_м)G² _V+(sin² _ср/К²_м)G² _изм+(sin² _ср/К²_м)G² _гку+G² _срп;

(2.59)

G² =G² _исх+(sin² _ср/К²_м)G² _V+(cos² _ср/К²_м)G² _изм+(cos² _ср/К²_м)G² _гку+G² _срп;

Так как погрешности ОНС имеют нормальный закон распределения, то можно использовать также средние и срединные E погрешности

_X,Y = 0.8G_X,Y; E _X,Y = 0.675G_X,Y. (2.60.)

2.4.2.Инерциальные навигационные системы (инс)

Появление инерциальных навигационных систем прежде всего объясняется стремлением осуществить с высокой точностью автономное определение местоположения объекта и параметров его движения. Практически реализовать ИНС оказалось возможным после известных успехов, достигнутых в производстве различных элементов инерциальных систем: гироскопов, акселерометров, следящих систем, счетно-решающих устройств, к точности которых предъявляются весьма высокие требования.

ИНС предназначена для определения местоположения объекта, параметров его движения, а в случае необходимости - для автоматического управления его движением.

В связи с этим ИНС должны решать следующие задачи:

1)Определять местоположение объекта;

2)Вырабатывать некоторые параметры для стабилизации объекта относительно его центра масс и удержания объекта на заданной траектории;

Для решения этих задач в ИНС должны определяться следующие данные: координаты местоположения ОН, составляющие его линейной скорости, курс, пройденное расстояние, боковое смещение центра тяжести от заданной траектории, высота. ИНС может работать в индикаторном режиме, когда она вырабатывает необходимые для навигации объекта данные, и в режиме управления, когда определяемые его данные используются для автоматического управления движением объекта.

Первичными измеряемыми величинами ИНС являются ускорения объекта, которые измеряются чувствительными элементами - акселерометрами, устанавливаемыми на гиростабилизированной площадке (ГСП), удерживающей их в определенном положении относительно инерциальной системы координат. Измеренные ускорения поступают в интеграторы, на выходе которых получаются составляющие линейной скорости объекта относительно инерциальной системы. С помощью счетно-решающих устройств эти составляющие пересчитываются в составляющие скорости объекта относительно Земли.

Последующее интегрирование составляющих скорости объекта при учете ряда поправок, вводимых счетно-решающим устройством на действие силы тяготения, на несферичность Земли и на действие других факторов, позволяет определить координаты объекта.

Наличие в инерциальной навигационной системе ГСП позволяет определять также углы поворота объекта относительно его центра масс. Если на ГСП установить третий акселерометр и его ось чувствительности направить по вертикали, то можно определить вертикальное ускорение объекта, а затем путем интегрирования вертикальную скорость и высоту места объекта.

Инерциальная система должна обеспечивать:

• высокую точность;

• большую чувствительность;

• возможность работы в течении продолжительного времени;

• широкий диапазон изменения входных величин;

• достаточно точную начальную установку ГСП относительно вертикали и в азимуте;

• высокую помехоустойчивость и независимость от наличия внешней информации;

• высокую ударную и вибрационную прочность, а также небольшой вес и габариты.

Существенным преимуществом ИНС по сравнению с другими навигационными системами является полная автономность: ИНС определяет координаты объекта и параметры его движения при отсутствии какой-либо связи с другими объектами или ориентирами. Инерциальная система позволяет полностью автоматизировать процессы навигации и может быть использована при различных режимах движения объекта. Система не требует наземных установок, в ней отсутствуют какие-либо радиоизлучения.

В инерциальных системах одним из основных элементов является гиростабилизированная площадка. В зависимости от расположения ГСП различают:

• ИНС с гиростабилизированной платформой, ориентированной по осям земной системы координат. ГСП стабилизирована относительно плоскости горизонта и заданного азимутального направления.

• ИНС с ГПС, ориентированной по осям инерциальной системы координат. ГСП сохраняет неизменное положение в инерциальном пространстве.

В состав любой ИНС входят следующие функциональные блоки и устройства:

• блок акселерометров;

• датчики угловой ориентации;

• задатчики первичной и исходной информации;

• счетно-решающие устройства;

• устройства отображения входной информации или выдачи выходных сигналов различным потребителям;

• устройства управления, настройки и коррекции погрешностей.

Для измерения вектора полного ускорения ā используются три одномерных (рис. 2.37,а) или один трехмерный акселерометры с ортогональными осями чувствительности.

Вектор измеренного ускорения в системе координат Oξηζ равен:

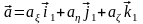(2.61)

,где i₁ ,,j₁ ,k₁ - орты системы координат Oξηζ .

Навигационное уравнение, учитывающее совокупность ускорений движений центра масс объекта, записывается в виде:

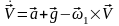(2.62)

,где 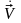- производная по времени от вектора скорости в системе координат Oξηζ, вращающегося с угловой скоростью ;

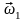ā - измеряется акселерометрами;

- гравитационное ускорение, не измеряемое акселерометрами;

- кориолисово ускорение (величину получают с датчиков ориентации, а величину получают, интегрируя сигналы акселерометров).

Гравитационное ускорение представим формулой:

(2.63)

,где GM - гравитационная постоянная;

R - расстояние от центра гравитации до объекта;

- единичный вектор направления R;

При установке акселерометров на ГСП моделирующую горизонтальную систему координат Oξηζ (рис. 2.37,а), совместим оси чувствительности акселерометров A_ξ ,A_η с горизонтальной плоскостью Oξη, а оси чувствительности акселерометра A_ζ - с направлением радиус вектора R.

Получаем:

(2.64)

Таким образом исключается действие гравитационного ускорения по осям Oξ и Oη.

Подобный способ компенсации гравитационных ускорений применяется в двумерных ИНС, предназначенных для счисления пути по координатам ξ и η.

Возможна компенсация вектора с использованием априорных данных.

Вектор меняется в зависимости от координат местонахождения объекта. На рис. 2.37,б показана принципиальная схема инерциальной системы в которой блок 1 акселерометров, совместно с датчиком угловой ориентации 5 измеряет вектор ā.

Абсолютное ускорение изменения местоположения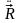 складывается из измеренного блоком акселерометров ускорения ā и действующего гравитационного ускорения :

(2.65)

Коменстор 2 форматирует по заданной программе вектор компенсационного гравитационного ускорения . Интегрируя в вычислителе 4 по времени получим на выходе измеренные векторы местонахождения 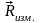и вектор скорости .

Условием абсолютной инвариантности инерциальной системы по отношению к гравитационному ускорению будет:

(2.66)

Неточная компенсация вызывает накопление погрешностей измерения и .

Рассмотрим принцип действия ИНС геометрического типа.

На стабилизаторе 1 (рис. 2.38), сохраняющем неизменным свое угловое положение относительно инерциального пространства, укреплена платформа 3 с акселерометром 4. Платформа 3 поворачивается при помощи привода 2 на углы, пропорциональные выходным сигналам двойного интегратора 5. Система координат OXYZ, связанная со стабилизатором, не вращается относительно инерциального пространства. С платформой 3 связана горизонтальная система координат O₁ξηζ, которая поворачивается относительно системы OXYZ на переносный угол , где 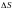- отрезок пути.

При движении объекта со скоростью V и перемещении системы из точки A в B возникает горизонтальное ускорение 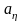и вертикальное ускорение . Двойной интеграл по времени от a_η равен пройденному пути:

(2.67)

Рассмотрим возмущенное состояние системы. Отклоним платформу от горизонтального положения на угол α (рис. 2.39). Если до наклона акселерометр измерял a_η, то в данном случае измеряемое ускорение вдоль наклонной оси OY₀ будет равно:

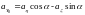(2.68)

а абсолютный угол поворота платформы с акселерометрами будет равен:

;

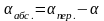(2.69)

Абсолютный угол поворота, платформы 3 приводом 2, будет равен:

(2.70)

где .

k_а- передаточный коэффициент акселерометра;

k_и- передаточный коэффициент интегратора;

k_п- передаточный коэффициент привода.

Используя (2.68) и (2.69) в (2.70) и учитывая, что , путем преобразований получим (при малых углах α).

(2.71)

Условием инвариантности к ускорениям гравитации является ренство 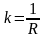.При этом условии собственное движение инерциальной системы определяется уравнением:

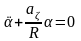(2.72)

При начальных условиях, когда t=0, и движение платформы относительно горизонтального положения будет представлять гармоническое колебание вида:

(2.73)

где - частота колебаний.

- период колебаний (2.74)

Скорость V и расстояние S отсчитываются соответственно по выходным сигналам первого и второго интеграторов. О пройденном расстоянии можно судить по углу поворота платформы с акселерометрами относительно стабилизатора, имея в виду, что .

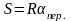Для поверхности Земли R=6371км и получаем период колебаний T=84,4мин, называемый периодом Шулера.

Рассмотрим принцип действия инерциальной системы полуаналитического типа.

В системе полуаналитического типа акселерометр жестко связан со стабилизатором и удерживается в горизонтальной плоскости. На рис. 2.40,а показан гиростабилизатор, управляемый сигналами, пропорциональными интегралу по времени от ускорений a_изм. . Акселерометр 2 укреплен на внутренний раме 3 гироскопа 4. Сигнал акселерометра после первого интегратора 1 подается на двигатель 5. Статор двигателя жестко укреплен на наружной раме 6 подвеса гироскопа, а ротор связан с осью вращения рамы 3. Момент двигателя вызывает скорость прецессии гироскопа вокруг оси ОХ. С выхода второго интегратора 7 получают расстояние .

Програмный компенсатор 8 вводит сигналы поправок. На рис. 2.40,б приведена структурная схема канала инерциальной системы.

Рассмотрим возмущенное состояние системы. Зададим гироплатформе угол наклона α относительно горизонта, так что 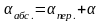. В результате акселерометр измерит ускорение a_Y.

Для инерциальной вертикали:

(2.75)

Для вычисления координаты:

(2.76)

Учитывая что и условие из уравнения (2.75) получим:

(2.77)

Погрешность исчисления координаты:

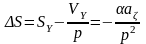(2.78)

При колебании вертикали погрешность координаты:

(2.78)

Широкое распространение получили бесплатформенные ИНС(БИНС). В такой системе (рис. 2.41) чувствительные элементы – акселерометр 1 и датчик угловой величины 2 – установлены на общем основании 3, жестко связанном с корпусом 5 объекта. Система координат OX₀Y₀Z₀ связана с основанием 3, а ось OY₀ совпадают с осью чувствительности акселерометра.

Датчик 2 измеряет абсолютные углы и угловые скорости поворота системы координат OX₀Y₀Z₀ относительно невращающейся системы координат OXYZ . Выходные сигналы чувствительных элементов f₁(t) и f₂(t) подаются в вычислитель 4, на выходе которого получаются сигналы, пропорциональные измеренным величинам – координате S и углу наклона α_изм. основания относительно горизонтальной оси Oη. Если акселерометр измеряет ускорение, определяемое формулой 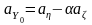, а датчик угловой величины измеряющую угловую скорость то полагая угол α малым, получим следующее выражение для выходных сигналов датчиков:

; (2.79)

Здесь две неизвестных величины – V и α. Решая совместно эти уравнения, получим:

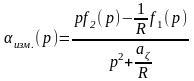; (2.80)

.

Аналитические зависимости (2.80), определяющие связь между входными f₁(t) и f₂(t) и выходными сигналами α_изм. и S, характеризуют алгоритмы вычислителя. Динамические свойства бесплатформенной инерциальной системы характеризуются передаточной функцией колебательного звена без демфирования и аналогичны свойствам рассмотренных здесь ранее инерциальных систем.

Однако, величины углов α в реальных условиях могут быть значительными и вычислитель 4 должен предусматривать решение нелинейной навигационной задачи. Кроме того следует иметь в виду, что в бесплатформенной схеме датчики угловых величин выступают в роли равнозначных датчиков углового вращательного движения наряду с акселерометром – датчиком поступательного движения. Это означает, что требования к точности и динамическим свойствам акселерометров и датчиков угловых величин должны быть достаточно высокими и равнозначными.

Погрешности ИНС обусловлены целым рядом причин методического и инструментального характера. К основным относятся причины, приводящие к неточности измерения ускорений объекта. Если ускорение измерено с ошибкой Δa, то при вычислении в ИНС скорости V объекта погрешность ΔV будет расти пропорционально времени t непрерывного вычисления, как следствие однократного интегрирования, а при счислении пройденного пути S погрешность ΔS будет расти пропорционально квадрату времени t непрерывного вычисления, как следствие двукратного интегрирования:

;

К ошибкам измерения ускорения могут привести кроме собственно ошибок акселерометра погрешности в установке акселерометра на объекте (непаралельность оси чувствительности акселерометра осям координат, относительно которых измеряется ускорение), неточность компенсации гравитационного ускорения, ошибки ввода начальных данных. Так, если начальные данные по координате Y вводятся с ошибкой ΔY_н, а по начальной скорости с ошибкой Δ , то погрешность счисления пути по координате Y будет:

(2.80)

ζ

A_ζ

A_η

O

η

R

A_ξ Платформа, стабилизи-

рованная в горизонталь-

ной плоскости.

ξ

Z

O₀

H

Σ

а.

3

1

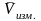
4

ā

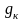
2

5

б.

Рис. 2.34. Принципиальные схемы учета гравитационных ускорений в инерциальных системах.

Рис. 2.37,а:

Oξηζ – система координат, связанная со стабилизированной в горизонтальной плоскости платформой;

O₀ΣΗΖ – cистема координат, связанная с центром гравитации;

A_ξ ,A_η,A_ζ - акселерометры, оси чувствительности которых совмещены с осями Oξηζ соответственно;

R – расстояние от центра гравитации до объекта.

Рис. 2.37,б:

1 – блок акселерометров;

2 – компенсатор;

4 – вычислители;

3 – сумматор;

5 – датчик угловой ориентации;

ā – ускорение;

g_к – компенсационное гравитационное ускорение;

, - измеренные скорость и расстояние R.

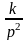
ζ

Z

1

a_ζ

Z

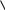
2

3

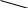
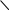
4

5

Y

A

R

Y

η

B

a_η

α_пер.

α_пер.

O

O₁

a

Рис. 2.38 Принцип работы одномерной ИНС геометрического типа.

1 – стабилизатор;

2 – привод;

3 – платформа;

4 – акселерометр;

5 – двойной интегратор;

Oξηζ – горизонтальная система координат;

OXYZ – система координат, связанная со стабилизатором 1;

A,B – последовательные положения ИНС геометрического типа при движении объекта;

α_пер. - угол переносного движения;

a_η,a_ζ – горизонтальное и вертикальное ускорения соответственно;

R – расстояние от центра гравитации до объекта;

a – измеренное ускорение.

ζ

a_ζ

Z₀

-a_ζsinα

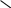
a_η

η

α

Y₀

a_ηcosα

Рис. 2.39 Измерение ускорения при отклонении от горизонта.

Oξηζ –горизонтальная система координат;

OX₀Y₀Z₀ – система координат, связанная с платформой;

a_η,a_ζ - горизонтальное и вертикальное ускорения соответственно;

a_ηcosα,-a_ζsinα – проекции горизонтального и вертикального ускорений соответственно;

α – угол отклонения платформы.

S_Y

2

1

ζ

η

7

8

O

Y

3

X

4

6

5

а.

S_Y

K₁

K₄

pV_Y

a_Y

α_абс.

αa_ζ

α

a_ζ

α_пер.

б.

Рис. 2.40. Схема одномерного ИНС полуаналитического типа.

Рис. 2.40,а:

1 – первый интегратор; 2 – акселерометр; 3 – внутренняя рама гироскопа; 4 – гироскоп; 5 – двигатель; 6 – наружняя рама подвеса гироскопа; 7 – второй интегратор; 8 – програмный компенсатор; OXYZ – система координат связанная с гироскопом;