1. Граничные условия I рода б) Однослойная цилиндрическая стенка

Р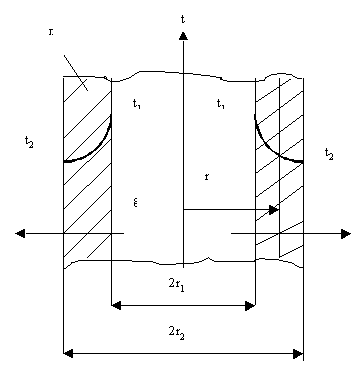 ассмотрим стационарный процесс теплопроводности в однослойной цилинд­рической стенке (трубе) с внутренним диаметром d₁ = 2r₁ и наружным диаметром d₂ = 2r₂ (рис.6).

На поверхностях стенки заданы постоянные температуры t₁ и t₂. Ко­эффициент теплопроводности в заданном интервале температур считаем постоян­ным. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.

Рис.6. Цилиндрическая стенка. Г.У. 1 рода.

В данной задаче дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе коор­динат. Так как q_v = 0 и ∂t/∂τ = 0, то поделив правую и левую часть уравнения (19) на а получим:

(46)

Ось трубы совмещена с осью Оz, т.е. при фиксированном радиусе температура вдоль трубы не изменяется, поэтому

(а)

Кроме того, т.к. температуры на наружной и внутренней по­верхностях трубы неизменны, изотермические поверхности являют­ся цилиндрическими, имеющими с трубой общую ось. Тогда темпера­тура не должна, зависеть от угла φ, т.е.

(б)

Следовательно, t есть функция только r, т.е. темпера­турное поле будет одномерным.

С учетом (а) и (б) уравнение (46) принимает вид:

(47)

Граничные условия:

при

при (48)

Совместное решение (47) и (48) дает уравнение температурного поля в цилиндрической стенке.

Для решения введем новую переменную:

,

тогда , (в)

Подставляя (в) в уравнение (47), получим:

(49)

Домножив левую и правую часть (49) на rdr, запи­шем

или (г)

Интегрируя (г), получим

(е)

Переходя к первоначальным переменным, перепишем (е) в виде:

или (50)

Разделив переменные и проинтегрировав (50), получим:

(51)

Определим постоянные интегрирования С₁ и С₂, подста­вив в уравнение (51) граничные условия:

при , отсюда

при , отсюда (д)

Решение уравнений (д) относительно С₁ и С₂ дает

,

Подставив значения С₁ и С₂ в уравнение (51), получим:

или (52)

Выражение (52) представляет собой уравнение логарифмической кривой, т.е. распределение температуры по толщине цилиндрической стенки является криволинейным.

Для нахождения теплового потока, проходящего через цилинд­рическую поверхность F, воспользуемся законом Фурье:

Из уравнения (50) значение температурного градиента:

Учитывая, что F = 2πrl, где l - длина трубы, получим

Заменив радиусы на диаметры, запишем:

(53)

Тепловой поток (53) может быть отнесен к единице внутренней поверхности, к единице наружной поверхности или к единице длины трубы.

При этом расчетные формулы для плотности теплового потока принимают вид:

_{, (54)}

где q₁, Вт/м² - плотность теплового потока для внутренней поверхности;

(55)

где q₂, Вт/м² - плотность теплового потока для наружной поверхности;

, (56)

где q_l, Вт/м² - линейная плотность теплового потока.

Линейная плотность теплового потока q_l - это количество тепла, которое проходит в единицу времени через стенку трубы длиной в 1 м в радиальном направлении.

Из уравнений (54) - (56) устанавливается связь между q₁, q₂ и q_l:

(57)