3.1.Анализ полученного решения.

Так как μ₁, μ₂, μ₃,…, μ_n представляет собой ряд возрастаю­щих чисел, то чем больше μ, тем меньше роль последующего члена ряда по сравнению с предыдущим. Кроме того, чем больше число F₀ , тем быстрее будут убывать члены ряда с увеличением n.

Многочисленные исследования показали, что уже при F₀≥0,3 ряд (99) становится настолько быстросходящимся, что распределе­ние температуры достаточно точно можно описать первым членом ряда:

(100)

или (101)

Величина D₁ является функцией только числа B_i и, как сказа­но выше, приводится в таблицах. Кроме того, если рассматривать температуру для определенного значения X , то и cos(μ₁*X ) становится функцией только числа B_i.

Для оси пластины Χ=х/δ=0 и сos(μ₁*0)=1,

Для поверхности пластины Χ=х/δ=1 и сos(μ₁*1)= сosμ₁

Для оси пластины произведение D₁cos(0)=D₁ обозначим как функцию N(B_i). Тогда уравнение (101) принимает вид:

(102)

Для поверхности пластины произведение D₁cosμ₁ обозначим как функцию P(B_i) и уравнение (102) запишется:

(103)

Функции N(B_i) и P(B_i) табулированы и для расчета могут быть взяты из справочников.

Из уравнения (99) следует, что при охлаждении (нагревании) пластины для любого момента времени при заданных граничных усло­виях поле температуры будет иметь вид симметричной кривой с максимумом на оси пластины (X=0). Для каждого последующего момента будет своя кривая, монотонно убывающая к поверхностям пластины. При этом для любого момента времени касательные к температурным кривым в точках X= ±1 проходят через две направляющие точки +А и –А, расположенные на расстоянии ±Х₀ от поверхности пластины, причем Х₀ =1/B_i (рис.12).

Для доказательства этого свойства рассмотрим температурное поле для произвольного момента времени F₀>0.

Умножив граничное условие (2.98) при x=δ на δ/θ₀, по­лучим:

Запишем последнее выражение в безразмерной форме:

(а)

Р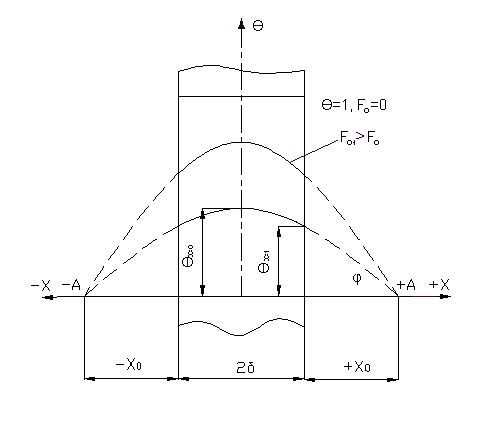 ис.12. Изменение температурного поля в неограниченной пластине при ее охлаждении.

Из рис.12 следует, что

(б)

Из выражения (а) и (б) получаем

Х₀ = 1/B_i (104)

Из уравнения (104) следует, что расстояние точки А от по­верхности пластины определяется заданными условиями однозначности, которые справедливы для любого момента времени. Сказанное справедливо не только для пластины, но и для цилиндра, шара и тел других геометрических форм.

Доказанное свойство температурных кривых дает возможность определить характер изменения температуры в теле при заданном значении числа B_i. Рассмотрим при этом три случая.

Рис.13.Распределение температуры при охлаждении пдастины.

1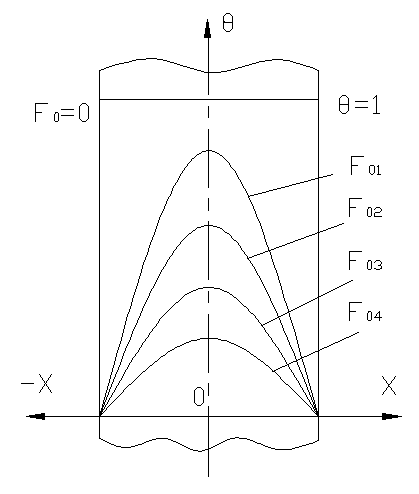 . B_i→∞ (практически B_i >100).

Если число B_i стремится к бесконечности, то температура поверх­ности пластины сразу становится равной температуре окружающей среды t_ж, в ко­торую помещена пластина.

Рис.14.Распределение

температуры при

охлаждении пластины.

Последнее следует из уравнения (104): при B_i→∞ Х₀=1/B_i=0. Это означает, что точка пере­сечения касательных к температурным кри­вым с осью X находится на поверхнос­ти пластины (рис.13). Из выражения для числа следует, что при за­данных конечных значениях δ и λ, B_i→∞ тогда, когда α→∞, т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физическими свойствами и разме­рами тела.

2. Очень малые числа B_i (практически B_i <0,1).

При малых числах B_i температура на по­верхности пластины незначительно отлича­ется от температуры на оси, т.е. темпе­ратура по толщине пластины распределяет­ся равномерно и кривая температур оста­ется почти параллельной оси ОХ для лю­бого момента времени (рис.14).

При B_i→0 Х₀=1/B_i→∞. Т.е. касательные к температурным кривым в точ­ках пересечения их с поверхностью должны пересекаться с осью абсцисс в бесконечности.

И з выражения видно, что малые значения числа B_i могут иметь мес­то при малых размерах толщины пластины δ, при больших значениях коэффициента теплопроводности λ и малых значениях коэффициента теплоотдачи α.

В рассматриваемом случае процесс охлаждения (нагрева) тела определяется интенсивностью теплоотдачи на поверхности пластины.

Иначе говоря, процесс выравнивания температуры в теле происходит существенно интенсивнее, чем отвод теплоты с поверхности. Задача становится внешней.

Рис.15. Распределе­ние

температуры при

охлаждении пластины

/3. Число B_i находится в пределах 0,1≤ B_i < 100.

В этом случае температурные кривие для любого момента времени будут выглядеть так, как показано на рис. 15.

Здесь интенсивность процесса охлаждения (нагревания) определяется как внутренним, так и внешним терми­ческим сопротивлением.

3.2 Графическое реше­ние задач нестационарной теплопровод­ности.

Как следует из уравнений (102) и (103), при заданной безразмерной координате X, безразмерная темпера­тура θ становится функцией только чисел B_i и F₀:

и

Логарифмируя уравнения (102) и (103), получим:

(105)

Из уравнений (105) следует, что при заданном значении X и заданном B_i натуральный логарифм θ линейно зависит от времени (числа Фурье). Последнее обстоятельство дает возможность графического решения уравнений (102) и (103). В справочной и учебной литературе приводятся графики зависимости θ от чисел B_i и F₀ для середины и поверхности пластины, которые имеют вид, представленный на рис. 16

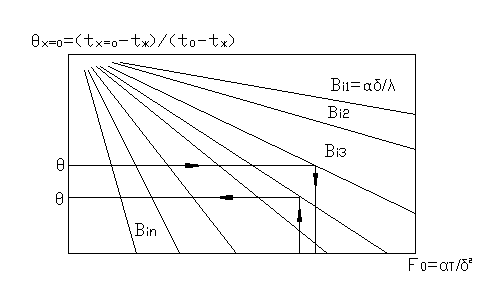
Рис.16. Зависимость θ=f₁(B_i, F₀) для середины пластины.

Порядок расчета температуры для середины пластины или для поверхности пластины (т.е. при X=0 илиХ=1) в заданный момент времени по графикам сводится к следующему:

1. Определяют число F₀ по заданным τ, а и δ;

2. Вычисляют число B_i по известным α, λ и δ;

3. На оси абсцисс графика откладывают найденное значение числа F₀, проводят вертикаль по наклонной прямой, соответствующей найденному значению B_i и, проектируя полученную точку на ось ординат, получают значение θ (рис.16).

4. По найденной безразмерной температуре θ_х=0 для середины пластины или θ_х=1 для поверхности пластины определяют исходную искомую температуру в середине пластины t_х=0 или на поверхности пластины t_х=δ.

С помощью указанных графиков можно решить обратную задачу: найти промежуток времени, необходимый для охлаждения (или нагре­вания) данной точки пластины (при X=0 или Х=1) до заданной температуры. В этом случае рассчитывают θ и B_i и по ним находят число F₀ (см.рис.16). По найденному числу F₀ вычисляют время τ.