- •4. Определение положения опасного сечения
- •5. Определение прогиба балки и угла поворота
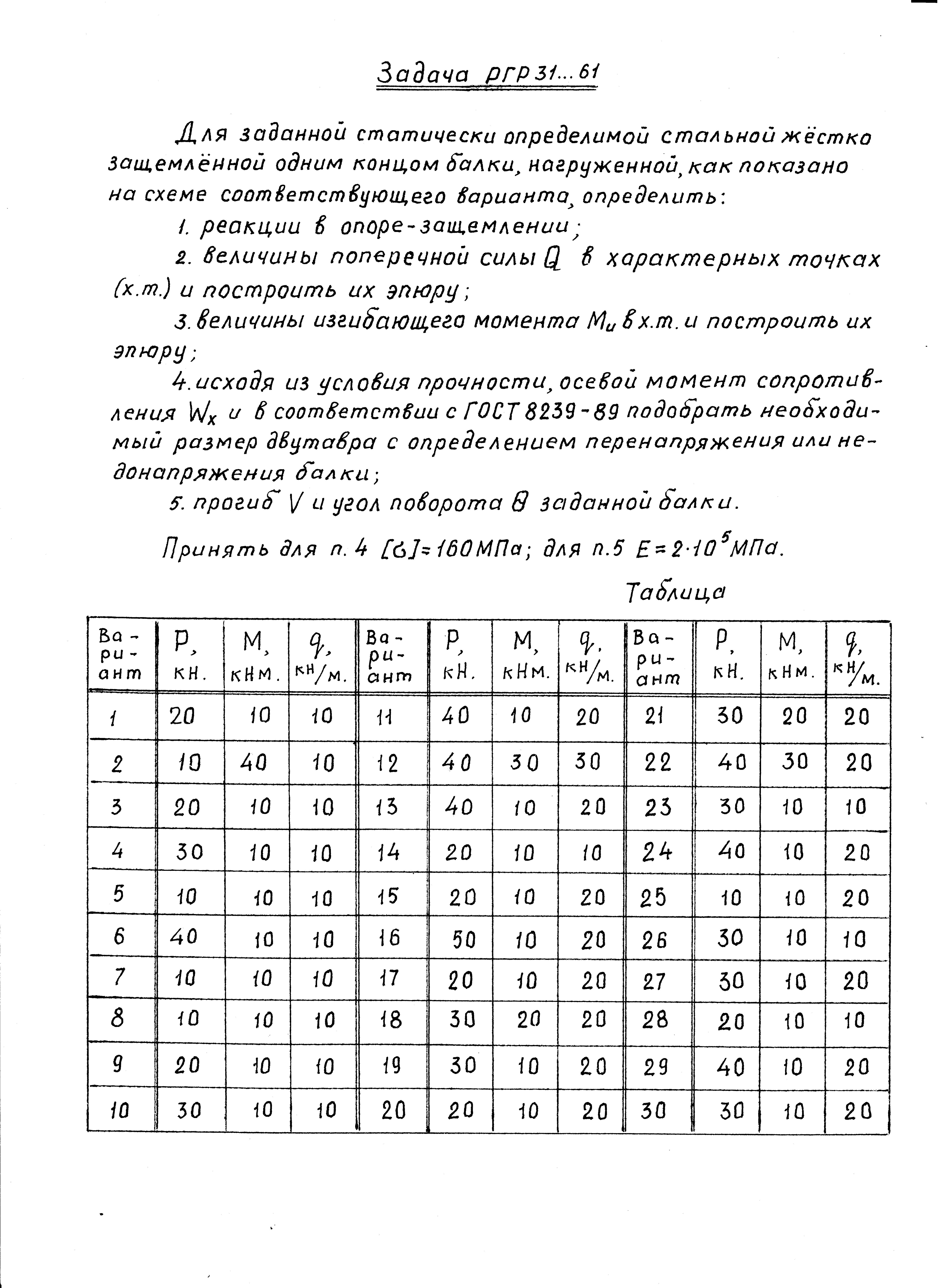
- •1. Определение реакций в опоре-защемлении.
- •2. Определение поперечной силы и построение её эпюры.
- •3. Определение изгибающего момента и построение его эпюры.
- •4. Определение положения опасного сечения и момента сопротивления .
- •5. Определение прогиба балки и угла поворота
5. Определение прогиба балки и угла поворота
в защемлении балки.
Для определения прогиба и угла поворота , в защемлённом конце балки, принимаем балку двухтаврового сечения, т.к. из всех рассмотренных ранее сечений двухтавровое сечение наиболее рационально.
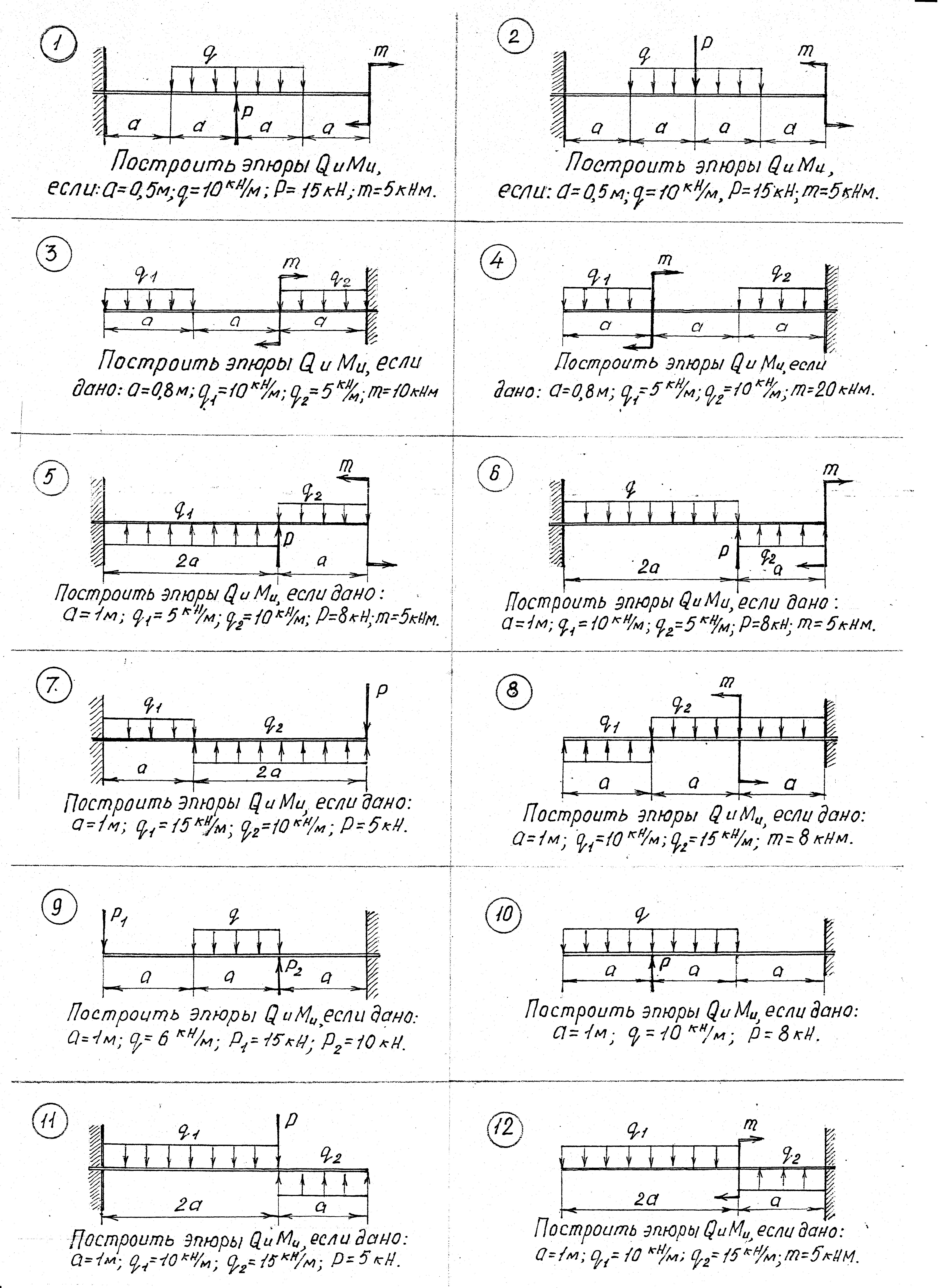
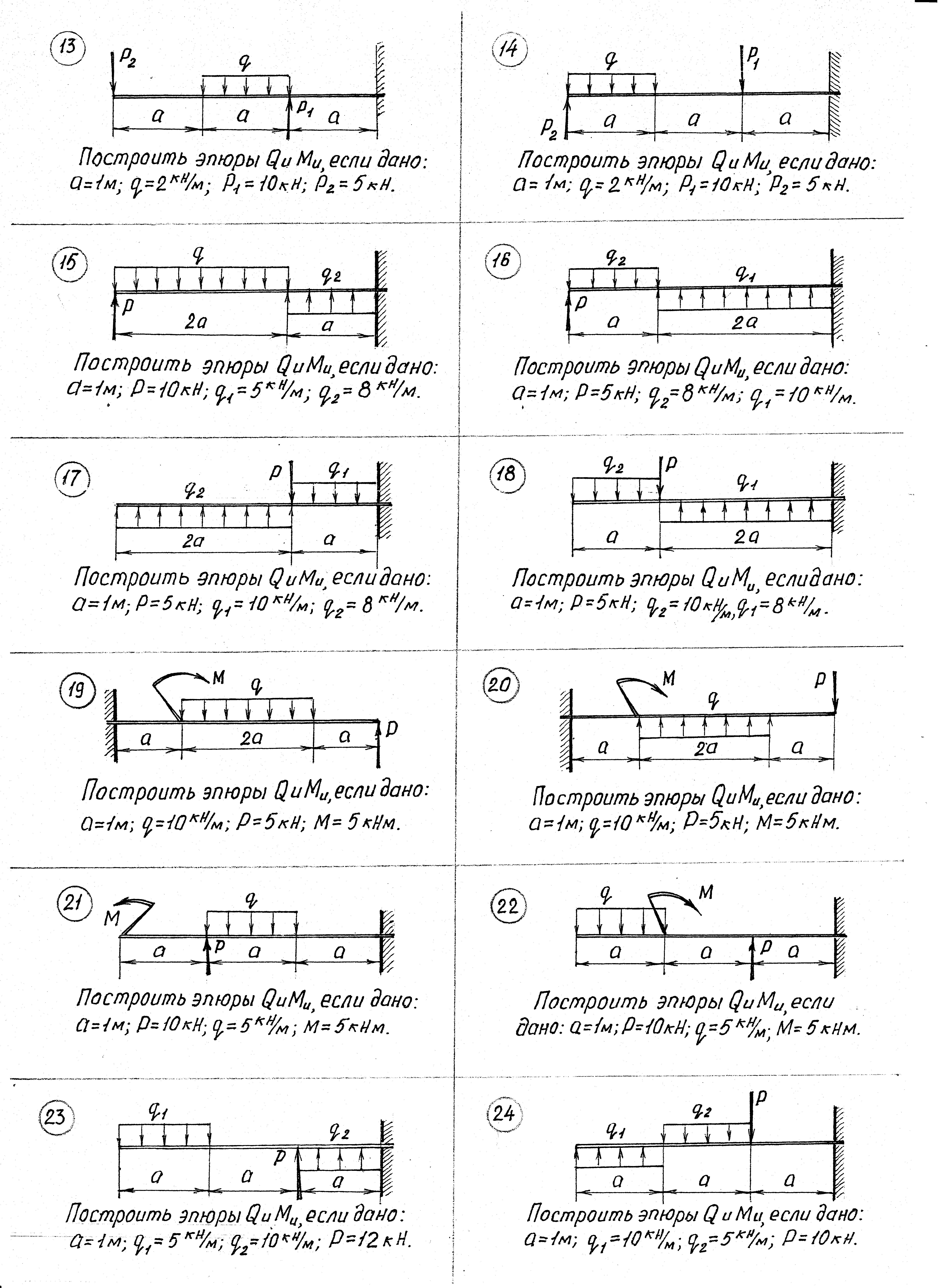
Вычерчиваем расчётную схему балки (см. рис. 2.2).
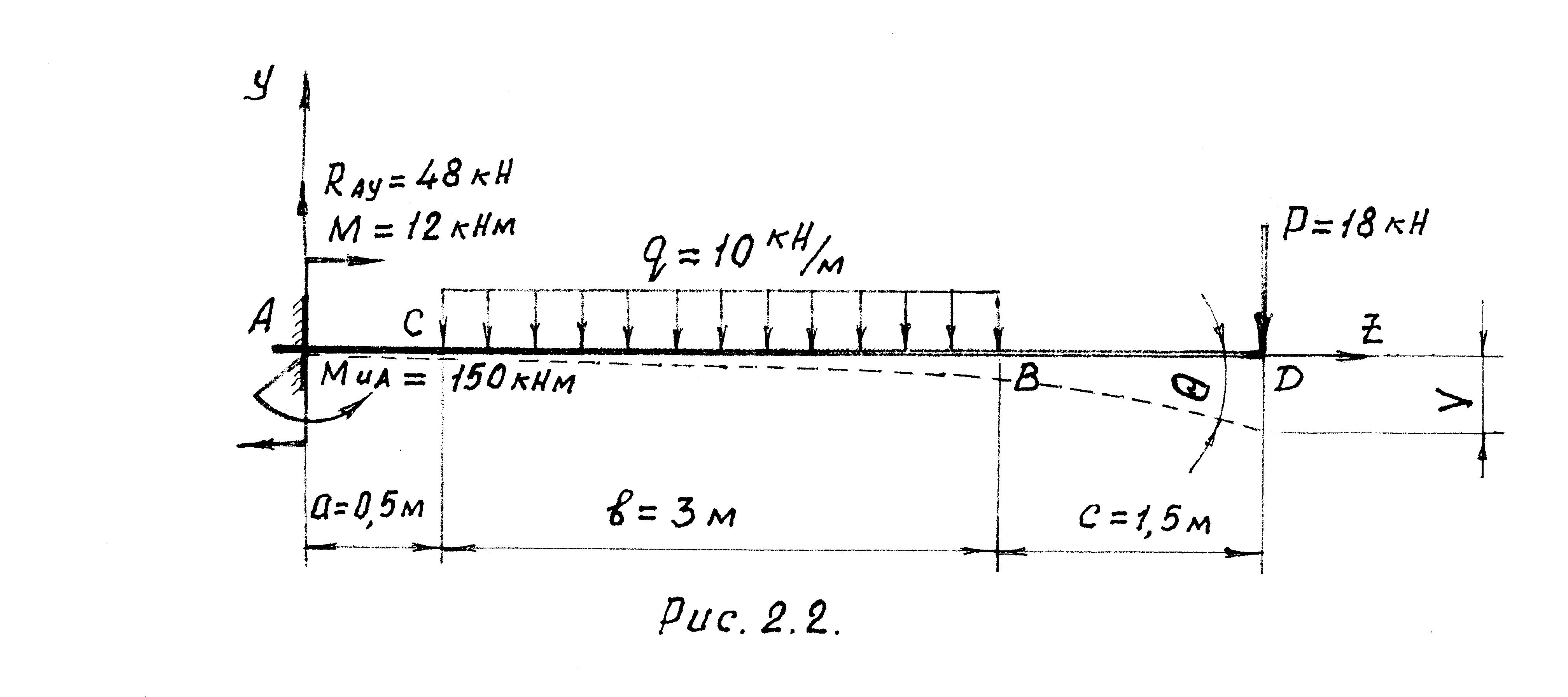
Используя принцип независимости действия сил и приложение 3, определяем величину прогиба и угла поворота в защемлении.
5.1. Определение прогиба от действия:
равномерно распределённой нагрузки интенсивностью
![]()
![]()
![]() .
.
Здесь
–
осевой момент инерции балки двухтаврового
сечения, который для двутавра N40
по ГОСТ 8239-89 равен
![]() .
.
Примечание. При подстановке числовых значений в формулу единицы измерений каждого силового параметра необходимо приводить к единой системе измерений.
сосредоточённой силы
![]()
![]()
![]() .
.
По принцыпу независимости действия сил полный перегиб балки составит
![]() .
.
5.2. Определение угла поворота от действия:
равномерно распределённой нагрузки интенсивностью
![]() .
.
сосредоточенной силы
![]()
Пары сил с моментом
![]() .
.
Полный угол поворота левого конца балки
![]() .
.
в градусах
![]() .
.
Заключение. По результатам решений задач 1 и 2 при условии одинакового нагружения балок вывод сделать самостоятельно.