НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
КОРАБЛЕСТРОЕНИЯ
имени адмирала Макарова.
Феодосийский политехнический
Институт
М Е Т О Д И К А
решения задач по курсу
„Сопротивление материалов”
Расчёт статически определимых
Балок, работающих на изгиб.
Модуль 5.
Преподаватель А.А. Чирков.
Феодосия-Николаев
2011г.
Обозначения и формулы применяемые в решении задач
статически определимых и не определимых балок
при деформации изгиба
Обозначения.
– площадь поперечного
сечения балки,
,
;
– сосредоточенная
сила, действующая на балку,
;
–
момент пары сил,
действующих на балку,
;
– интенсивность
равномерно распределённой нагрузки
действующей
на балку,
;
,
– реакции опор балки соответственно
и
,
;
– момент
противодействия балки внешним нагрузкам,
;
– поперечная
перерезывающая сила, возникающая в
сечениях
балки от действия внешних нагрузок, ;
– характерные
точки балки, т.е. точки, в которых приложены
внешние нагрузки, а также начало и конец действия
равномерно распределённой нагрузки;
– допускаемое
напряжение материала балки,
;
– модуль упругости
материала балки,
;
– осевой момент
сопротивления балки,
;
–
момент инерции
балки,
;
– стрела поворота
балки,
,
;
– угол поворота
балки,
;
– угол поворота
балки,
.
Формулы.
1.
–
условие прочности балки, работающей
на изгиб.
2.
– осевой момент сопротивления круглого
сечения.
3.
–
осевой момент сопротивления прямоугольного
сечения.
4.
– пределение перенапряжения
или
недонапряжения
балки,
работающей на изгиб.
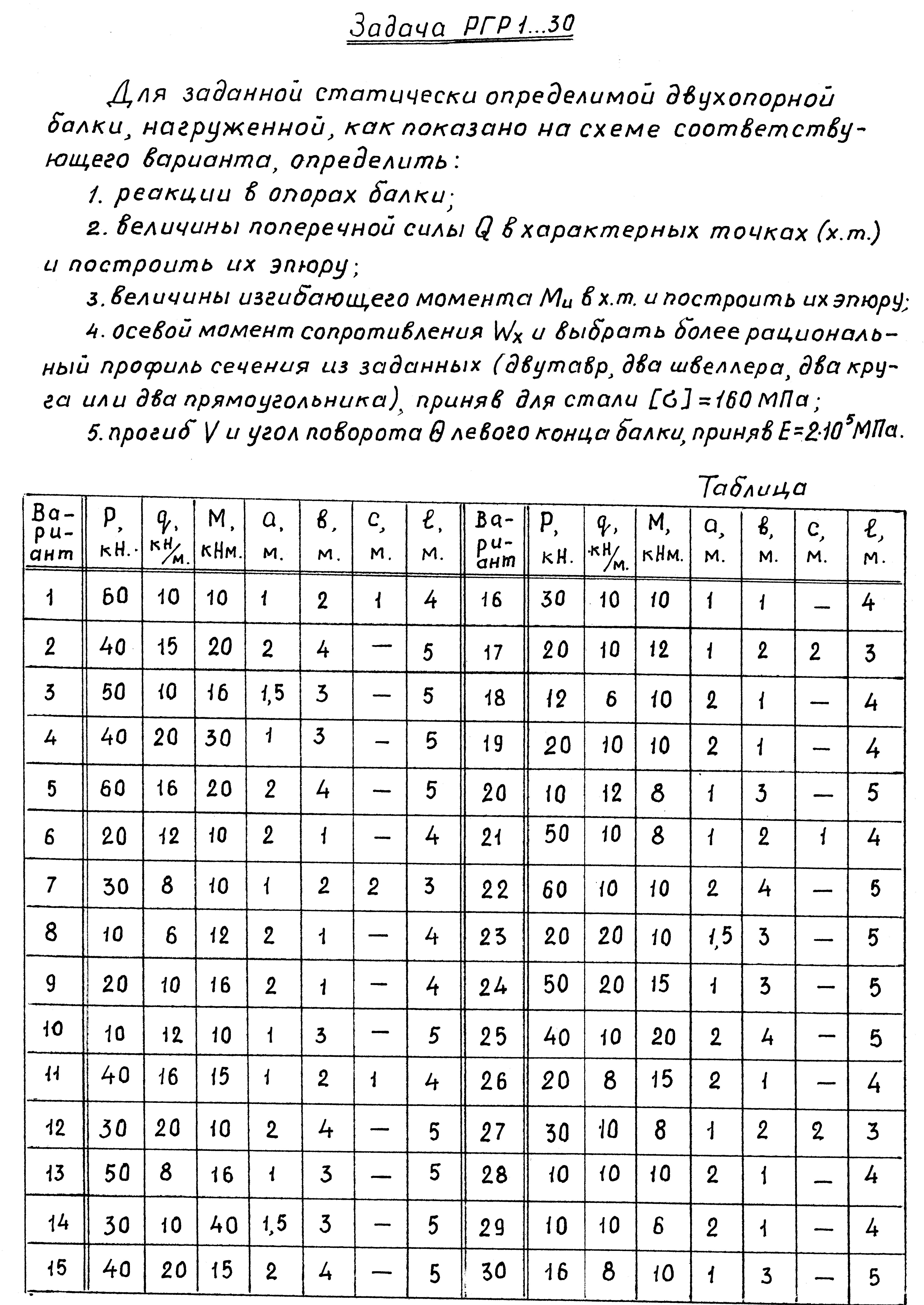
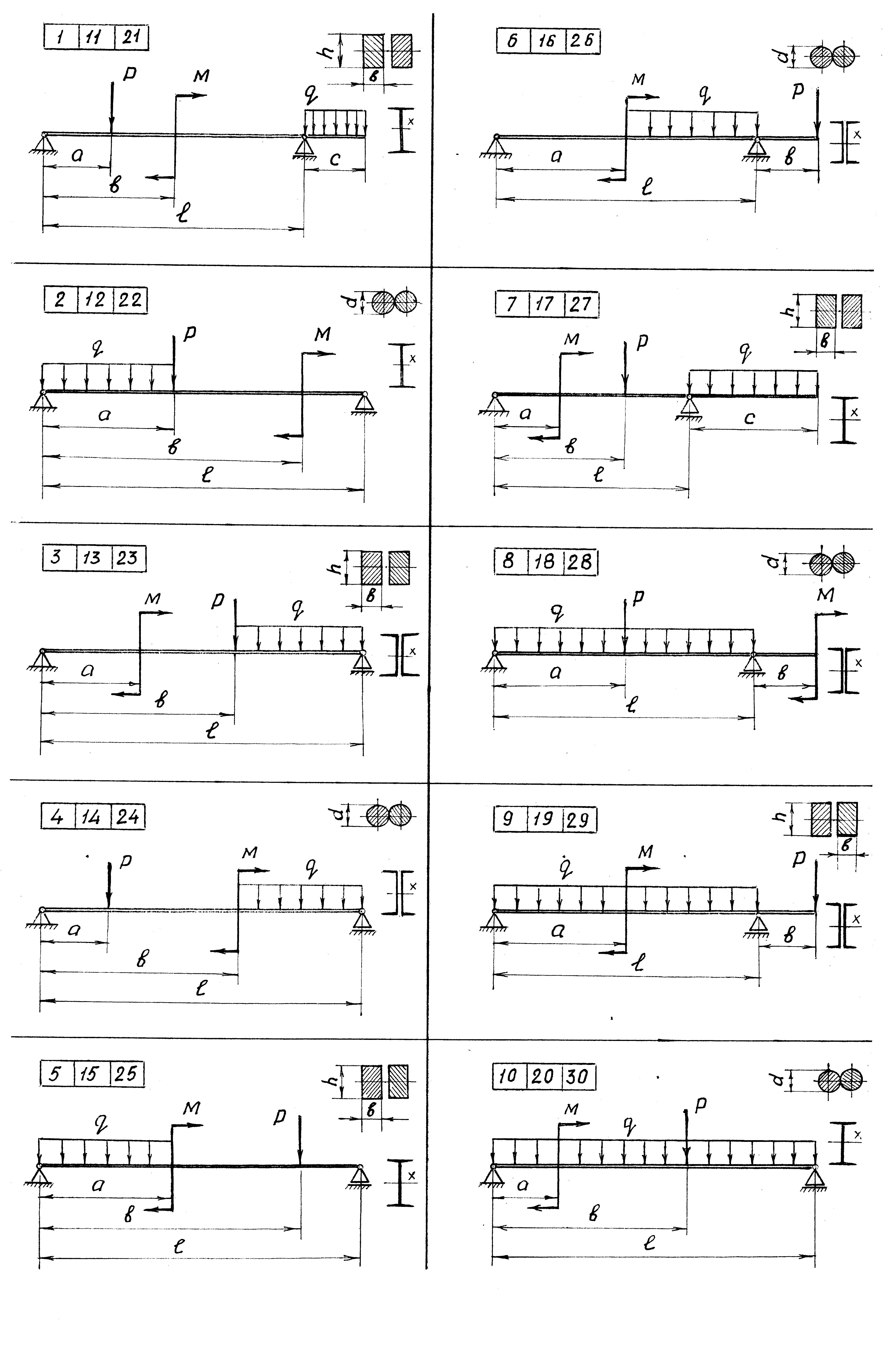
Задача 5.1. Расчёт статически определимой балки
при прямом изгибе
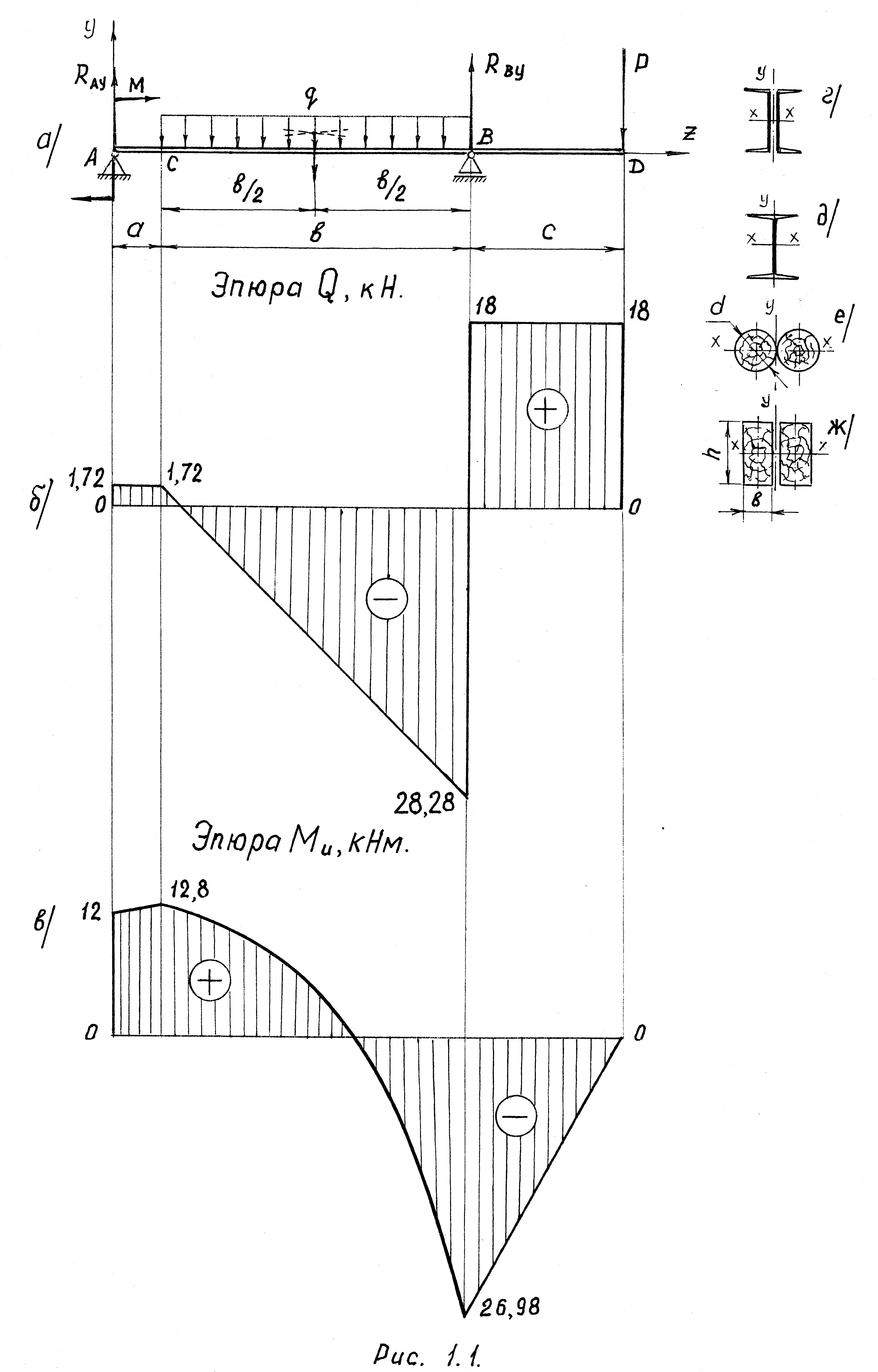
Для заданной двухопорной балки, нагруженной, как показано на рис 1.1,а, определить:
1. реакции в опорах балки;
2. величины поперечной
силы
в характерных точках
и построить эпюру;
3. величины изгибающего момента в характерных точках и построить эпюру;
4. положение опасного сечения балки и осевого момента сопротивления , руководствуясь условием прочности, и выбрать более рациональный профиль сечения из данных (см. рис. 1.1, г,д,е,ж);
5. прогиб балки и угла поворота левого конца балки .
Исходные данные.
Схема нагружения балки (см. рис. 1.1,а);
;
;
;
;
;
;
Допускаемое
напряжения: для стали
;
для дерева
;
модуль продольной
упругости для стали
.
Примечание. Модуль продольной упругости для дерева при необходимости принять
по приложению 1.
Решение.
Вычерчиваем заданную схему нагружения двухопорной балки с обозначением реакции, возникающих в опорах от действия внешних нагрузок , , (см. рис. 1.1, а).
1. Определение реакций в опоре.
Обозначим левую и правую опоры соответственно и и обозначим реации этих опор и , возникающих от действия внешних нагрузок, предварительно направив вектора их действия вверх.
Исходя из условий равновесия балки, можно записать:
равновесие относительно левой опоры А
;
;
;
;
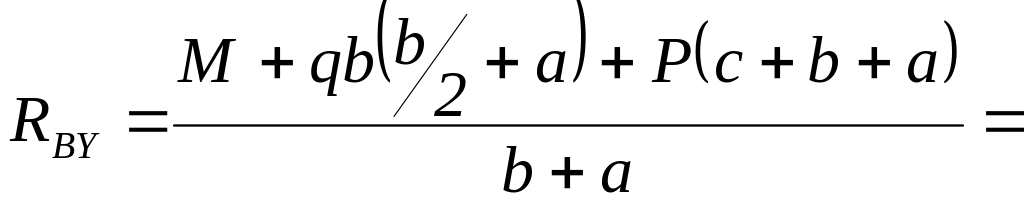
Равновесие относительно правой опоры В
;
;
;
.
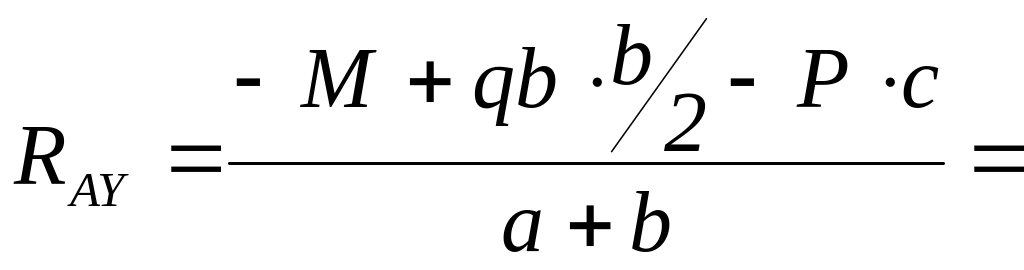
Проверка.
Проверку выполняем также исходя из
условия равновесия балки, но через сумму
проекции на ось
всех сил.
;
;
.
Вывод. Реакции
опор
и
и
предварительное направление их действия
определены верно.
Примечание. Если бы одна из реакций или обе получились бы отрицательными, то направление их действия следовало бы изменить на противоположное, а полученные числовые значения принять по модулю.
2. Определение поперечной силы и построение её эпюры.
Намечаем характерные точки A, B, C и D по длине балки. Характерные точки, как правило, намечают в точках приложения сосредоточенных нагрузок, а также в начале и конце действия равномерно распределённой нагрузки интенсивностью .
Применяя метод поперечных сечений, определяем величину поперечной силы, т.е. слева и справа от каждой
Сечение по
А, т.е. при
;
;
Сечение по
С слева,
;
;
Сечение по
С справа,
;
;
Сечение по
В слева,
;
;
Сечение по
В справа,
;
;
Сечение по
D, т.е. при
;
.
Если отсечь балку
по пролёту ˝С˝, отбросить мысленно
её левую часть и рассмотреть оставшуюся
правую, то видим, что
,
т.е. результат остаётся прежним (более
подробно см. ˝Обобщённые правила
построения эпюр при различных видах
деформации˝).
По полученным результатам расчёта строим эпюру поперечной силы , кН (см. рис. 1.1, б).
3. Определение изгибающего момента и построение его эпюры.
Применяя тот же метод сечений в тех же характерных точках, что и для определения , находим величины изгибающих моментов с последующим построением эпюры .
Сечение по
А, т.е. при
;
;
Сечение по
С, т.е. при
;
;
Сечение по
В, т.е. при
;
;
Сечение по
D, т.е. при
;
.
В данном случае рассматривается правая
отсечённая часть по пролёту балки длиной
равной ˝С˝. С целью проверки рассмотрим
левую отсечённую часть по данному
пролёту приблизились
D, т.е.
.
.
Разница в
является
результатом округлений в ранее выполненных
расчётах, что практически допускается
(более подробно см. ˝Обобщённые правила
построения эпюр при различных видах
деформации˝).
По результатам
расчётов строим эпюру изгибающего
момента
по длине балки (см. рис. 1.1, в).
4. Определение положения опасного сечения
и момента сопротивления .
4.1. Анализируя
построенные эпюры
и
(рис. 1.1, б,в), видим, что опасным
является сечение по
В, в котором
и
.
4.2. Исходя из условия прочности при деформации изгиба
,
определяем момент сопротивления балки
.
4.3. Определение основных параметров сечения балки состоящих из:
4.3.1. Дух швеллеров (см. рис 1.1,г):
поскольку балка состоит из двух швеллеров, то осевой момент сопротивления одного швеллера от расчётного составит:
.
По ГОСТ 8240-89 выбираем швеллер N16, у которого:
момент сопротивления
–
;
площадь поперечного
сечения –
масса одного
погонного метра –
.
4.3.2. Одного двутавра (см. рис. 1.1, д):
По расчётному
значению осевого момента сопротивления
и ГОСТ 8240-89 выбираем швеллер N20,
у которого:
момент сопротивления
–
;
площадь поперечного
сечения –
масса одного
погонного метра –
.
4.3.3. Двух круглых деревянных брусьев (см. рис. 1.1, е):
определяем осевой момент сопротивления деревянной балки
.
Поскольку балка состоит из двух круглых брусьев, то осевой момент сопротивления одного бруса составит:
.
Определяем диаметр одного бруса, исходя из условия:
,
откуда получим
.
Принимаем
.
Определяем осевой момент сопротивления одного круглого бруса по расчётно-принятому диаметру:
.
4.3.4. Двух деревянных
брусьев прямоугольного сечения со
сторонами
(см.
рис. 1.1, ж);
Момент сопротивления балки принимаем по п.п. 4.3.3, т.е.
Момент сопротивления одного бруса балки
,
при этом
;
отсюда получим
.
Полученное значение округляем в большую сторону до ближайшего чётного числа или числа оканчивающегося на пять.
В данном случае
принимаем:
.
Осевой момент сопротивления по принятым значениям сторон одного прямоугольного бруса составляет:
Полный момент сопротивления балки составит:
.
4.3.5. Площадь поперечного сечения деревянной балки составленной:
из двух круглых брусьев
;
из двух прямоугольных брусьев
.
4.3.6. Определение перенапряжения или недонапряжения каждого из видов балок.
Балка стальная составленная из двух швеллеров
Балка стальная двухтавровая
Из приведённых
расчётов видно, что балка двухтавровая
меньше недонапряжена (недогруженна), в
легче балки из двух швеллеров и проще
по конструкции. Следовательно принятие
двухтавровой балки более целесообразна.
Балка составленная из двух брусьев
Балка составленная из брусьев прямоугольного сечения
Отношение площадей поперечных сечений
.
Балка из круглых
брусьев в
тяжелее балки из прямоугольных брусьев,
но её работа на
эффективнее
.
5. Определение прогиба балки и угла поворота
левого конца балки (опора А).
Для определения прогиба и угла поворота выбираем двухтаврового сечения.
Вычерчиваем расчётную схему балки (см. рис. 1.2).
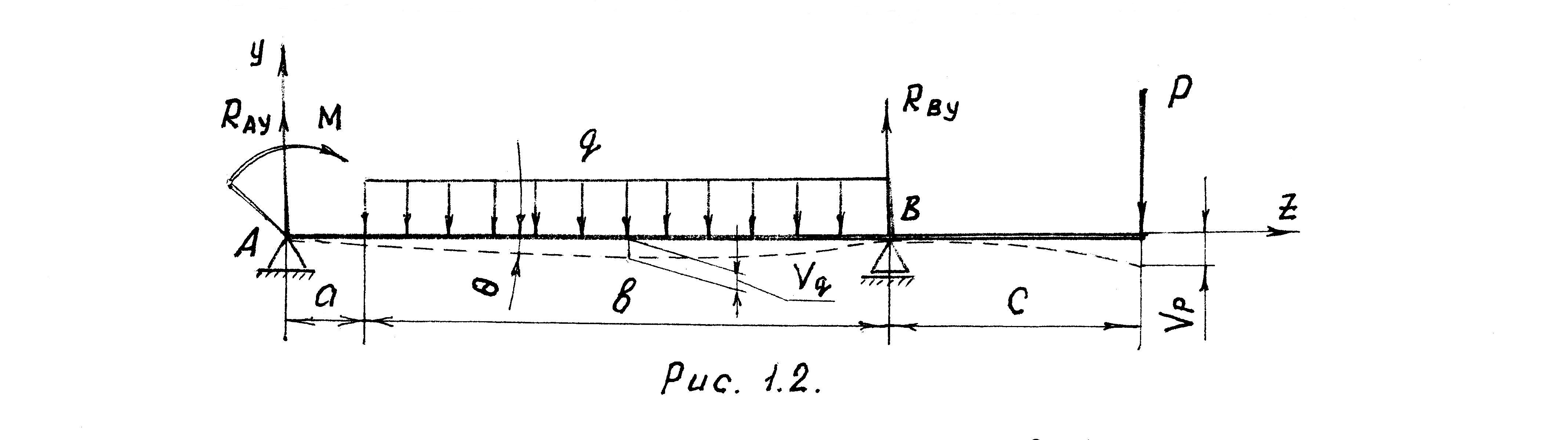
Используя принцип независимости действия сил и приложение 3, определяем величину прогиба и угла поворота от действия каждого силового фактора.
5.1. Определение прогиба от действия:
равномерно распределённой нагрузки интенсивностью
.
сосредоточённой силы
.
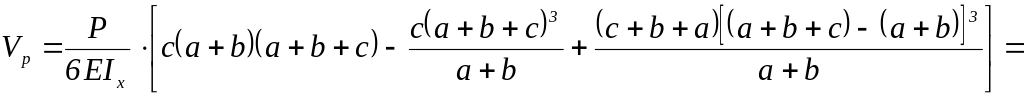
Полный перегиб балки
.
Здесь – осевой момент инерции балки двухтаврового сечения, значение которого принято по ГОСТ 8239-89 (см. приложение 2).
Для двухтавра N20
.
5.2. Определение угла поворота от действия:
равномерно распределённой нагрузки интенсивностью
.
Сосредоточенной силы
.
активного изгибающего момента в опоре
Полный угол поворота левого конца балки
.
в градусах
.
Напоминание. Следует помнить, что исходные данные и параметры, получаемые в результате вычислений, следует приводить к единой системе измерений.
Задача 5.2. Расчёт статически определимой
жёстко защемлённой балки при прямом изгибе.
Для банной жёстко защемлённой балки (см. рис. 2.1, а), определить те же параметры по тем же исходным данным, которые изложены в задаче 1. Сравнить результаты расчётов, сделать выводы.
Решение.
Вычерчиваем схему нагружения балки с обозначением реакций и с предполагаемым направлением их действия (см. рис. 2.1, а). Реакции и возникают в жёсткой опоре-защемлении в результате действия на балку сосредоточенной силы , равномерно распределённой нагрузки с интенсивностью и действия внешнего активного изгибающего момента непосредственно на опору-защемление.