
- •Практическая работа №1
- •Если с – постоянная величина, то .
- •Практическая работа №2
- •Практическая работа №3
- •Практическая работа №4
- •Практическая работа №5
- •Направление выпуклости графика функции
- •Точки перегиба
- •Асимптоты
- •Практическая работа №6
- •Общая схема построения графиков функций
- •Практическая работа №7
- •Практическая работа №8
- •Практическая работа №9
- •Практическая работа №10
- •Практическая работа №11
- •Практическая работа №13
- •Практическая работа №14
- •Решение системы трех линейных уравнений с тремя неизвестными.
Практическая работа №8
Предмет: «Элементы высшей математики»
Тема: «Вычисление неопределенных интегралов методом интегрирования по частям»
Цель: Научиться вычислять интегралы методом интегрирования по частям
Краткая теория:
Функция называется первообразной для функции в промежутке , если в любой точке этого промежутка ее производная равна : .
Отыскание первообразной функции по заданной ее производной называется интегрирование. Совокупность первообразных для функции или для дифференциала называется неопределенным интегралом и обозначается символом . Таким образом, .
Основные свойства неопределенного интеграла
Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная: .
Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: .
Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций: .
Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла: .
Если и ‑ любая известная функция, имеющая непрерывную производную, то .
Основные формулы интегрирования
;
, ;
;
;
;
;
;
;
.
Метод интегрирования по частям

Пример
1.
Найти интеграл
 .
.
Решение.


Ход работы:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
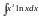 ;
5)
;
5)
 ;
6)
;
6)
 ;
7)
;
7)
 .
.
Контрольные вопросы
Напишите формулу метода интегрирования по частям.
Перечислите основные свойства неопределенного интеграла.
Практическая работа №9
Предмет: «Элементы высшей математики»
Тема: Вычисление определенных интегралов
Цель: Научиться вычислять производные высших порядков
Краткая теория:
Для
вычисления определенного интеграла от
функции
 в том случае, когда можно найти
соответствующий неопределенный интеграл
в том случае, когда можно найти
соответствующий неопределенный интеграл
 ,
служит формула
Ньютона-Лейбница:
,
служит формула
Ньютона-Лейбница:

 ,
т.е. определенный интеграл равен разности
значений первообразной при верхнем и
нижнем пределах интегрирования.
,
т.е. определенный интеграл равен разности
значений первообразной при верхнем и
нижнем пределах интегрирования.
Ход
работы: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
Самостоятельная работа
I вариант |
II вариант |
Вычислить определенные интегралы |
|
1.
|
1.
|
2.
|
2.
|
3.
|
3.
|
4.
|
4.
|
5.
|
5.
|
Контрольные вопросы:
Какие табличные интегралы используются при решении интегралов из самостоятельной работы?
Решение каких заданий требует использование метода замены переменной?
Какие еще методы интегрирования вам знакомы?
Практическая работа №10
Предмет: «Элементы высшей математики»
Тема: Решение прикладных задач с помощью определенного интеграла
Цель: Научиться решать прикладные задачи с помощью определенного интеграла
Краткая теория:
Определенный
интеграл широко применяется при
вычислениях различных геометрических
и физических величин. Вычисление
некоторой величины u,
соответствующей промежутку
 изменения независимой переменной x,
выполняется по следующей схеме:
изменения независимой переменной x,
выполняется по следующей схеме:
Пусть величина u получает приращение
 ,
соответствующие изменению x
на малую величину
,
соответствующие изменению x
на малую величину
 ;
рассматривается как данная или
определяемая из условия задачи функция
от x
(рис. 1).
;
рассматривается как данная или
определяемая из условия задачи функция
от x
(рис. 1).Заменив приращение
 дифференциалом
дифференциалом
 (главная часть приращения
)
и
- дифференциалом
(главная часть приращения
)
и
- дифференциалом
 ,
получим
,
получим
 .
.Интегрируя это равенство в пределах от
 до
до
 ,
находим
,
находим
 .
.

Ход
работы.
Вычислить площади фигур, ограниченные
линиями: 1)
 ,
,
 ,
,
 ,
,
 ;
2)
;
2)
 ,
,
,
,
 ;
3)
;
3)
 ,
,
,
,
 ,
;
4)
,
;
4)
 ,
.
,
.
Самостоятельная работа:
I вариант |
II вариант |
Вычислить площади фигур, ограниченные линиями: |
|
1.
|
1.
|
2.
|
2.
|
3.
,
,
,
|
3. , , , . |
4.
|
4.
|
Контрольные вопросы:
Что называют определенным интегралом?
Какая формула обычно используется для вычисления определенных интегралов?











 ,
,
,
.
,
,
,
. ,
,
,
.
,
,
,
. ,
,
.
,
,
. ,
,
.
,
,
. .
. ,
.
,
. ,
.
,
.