Практическая работа №6
Предмет: «Элементы высшей математики»
Тема: «Исследование функции по общей схеме»
Цель: научиться исследовать функцию по общей схеме.
Краткая теория:
Общая схема построения графиков функций
Найти область определения функции.
Выяснить, не является ли функция четной, нечетной или периодической.
Функция
называется четной,
если при всех значениях х
и области определения этой функции
.
Функция
называется нечетной,
если при всех значениях х
и области определения этой функции
.
Функция
называется периодической,
если существует такое число
,
что при любом α
из области определения функции числа
и
также принадлежит этой области и
выполняется равенство
.
Найти точки пересечения графика с осями координат (если это не вызывает затруднений).
Найти асимптоты графика функции.
Найти промежутки монотонности функции и ее экстремумы.
Найти промежутки выпуклости графика функции и точки перегиба.
Построить график, используя полученные результаты.
Пример
1.
Построить график функции
.
Решение.
1. Функция определена на всей числовой
прямой, т.е.
.
2. Данная функция не является четной, ни
нечетной; кроме того, она не является
периодической. 3. Найдем точку пересечения
графика с осью Оу:
пологая
,
получим
.
Точки пересечения графика с осью Ох
в данном случае затруднительно. 4.
Очевидно, что график функции не имеет
асимптот. 5. Найдем производную:
.
Далее, имеем
,
следовательно
,
.
Точки
и
делят ООФ на три промежутка. В промежутках
и
,
т.е. функция возрастает, а в промежутке
,
т.е. функция убывает.
,
.
6. Найдем вторую производную:
;
,
.
Точка
делит ООФ на два промежутка
и
.
В первом из них
,
а во втором
т.е. в промежутке
кривая выпукла вверх, а в промежутке
выпукла вниз. Т.о., получаем точку перегиба
(2; ‑1). 7. Используя полученные данные,
строим искомый график.
Ход
работы:
Исследуйте следующие функции и постройте
их графики: 1)
;
2)
;
3)
;
4)
;
5)
.
Контрольные вопросы:
Какая функция называется четной?
Какая функция называется нечетной?
Какая функция называется периодической?
Практическая работа №7
Предмет: «Элементы высшей математики»
Тема: «Вычисление неопределенных интегралов методом непосредственного интегрирования и методом введения новой переменной»
Цель: Научиться вычислять интегралы методом непосредственного интегрирования и методом введения новой переменной
Краткая теория:
Функция
называется первообразной
для функции
в промежутке
,
если в любой точке этого промежутка ее
производная равна
:
.
Отыскание
первообразной функции по заданной ее
производной называется интегрирование.
Совокупность первообразных для функции
или для дифференциала
называется неопределенным интегралом
и обозначается символом
.
Таким образом,
.
Основные свойства неопределенного интеграла
Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:
.Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
.Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:
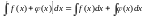.Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:
.Если
и
‑ любая известная функция, имеющая
непрерывную производную, то
.
Основные формулы интегрирования
;
,
;
;
;
;
;
;
;
.
Пример
1.
Найти интеграл
.
Решение.
Пример
2.
Найти интеграл
.
Решение.
Пример
3.
Найти интеграл
.
Решение.
Ход
работы: 1)
;
2)
;
3)
;
4)
;
5)
.
Самостоятельная работа
I вариант |
II вариант |
Найти интегралы |
|
1.
|
1.
|
2.
|
2.
|
3.
|
3.
|
4.
|
4.
|
5.
|
5.
|
Контрольные вопросы
Что называется первообразной?
Что называется интегрированием?
Какие из интегралов самостоятельной работы вычисляются методом введения новой переменной?