
- •Практическая работа №1
- •Если с – постоянная величина, то .
- •Практическая работа №2
- •Практическая работа №3
- •Практическая работа №4
- •Практическая работа №5
- •Направление выпуклости графика функции
- •Точки перегиба
- •Асимптоты
- •Практическая работа №6
- •Общая схема построения графиков функций
- •Практическая работа №7
- •Практическая работа №8
- •Практическая работа №9
- •Практическая работа №10
- •Практическая работа №11
- •Практическая работа №13
- •Практическая работа №14
- •Решение системы трех линейных уравнений с тремя неизвестными.
Практическая работа №3
Предмет: «Элементы высшей математики»
Тема: Вычисление производных сложных и обратных тригонометрических функций
Цель: Научиться вычислять производных сложных и обратных тригонометрических функций
Краткая теория:
Пусть
функция
определена в некоторой окрестности
точки
.
Предел отношения приращения
функции в этой точке (если он существует)
к приращению
аргумента, когда
 ,
называется производной функции
в точке
.
,
называется производной функции
в точке
.
Таким
образом,
 .
Вычисление производной называется
дифференцированием
функции.
.
Вычисление производной называется
дифференцированием
функции.
Таблица производных

 ;
; (где
(где
 );
в частности,
);
в частности,
 ;
; ,
,
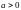 ;
в частности,
;
в частности,
 ;
; ,
,
,
,
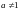 ;
в частности,
;
в частности,
 ;
;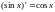 ;
; ;
; ;
; ;
; ;
; ;
; ;
;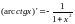 .
.
Основные правила дифференцирования
Пусть
с
– константа, а
 и
и
 имеют производные в некоторой точке х.
Тогда
имеют производные в некоторой точке х.
Тогда
 ;
; ,
частности,
,
частности,
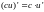 ;
; ,
в частности,
,
в частности,
 ;
; .
.
Пример
1.
Найти
производную функции
 .
.
Решение.


Пример
2.
Найти
производную функции
 .
.
Решение.


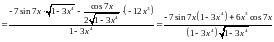 .
.
Пример
3.
Найти
производную функции
 .
.
Решение.
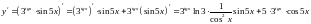 .
.
Пример
4.
Найти
производную функции
 .
.
Решение.
 .
.
Самостоятельная работа
I вариант |
II вариант |
Найти производные функций |
|
1.
|
1.
|
2. y=2arctg x arcsin 2x |
2. y=esin x arctg 3x |
3. y=ln cos 6x |
3. y=sin ln 7x |
4.
|
4.
|
Контрольные вопросы
Какие правила дифференцирования используются в каждом из заданий самостоятельной работы?
Практическая работа №4
Предмет: «Элементы высшей математики»
Тема: Вычисление второй производной и производных высших порядков
Цель: Научиться вычислять производные высших порядков
Краткая теория:
Пусть
функция
определена в некоторой окрестности
точки
.
Предел отношения приращения
 функции в этой точке (если он существует)
к приращению
функции в этой точке (если он существует)
к приращению
 аргумента, когда
аргумента, когда
 ,
называется производной функции
в точке
.
,
называется производной функции
в точке
.
Таким образом, . Вычисление производной называется дифференцированием функции.
Таблица производных
 ;
; (где
(где
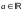 );
в частности,
);
в частности,
 ;
; ,
,
 ;
в частности,
;
;
в частности,
;, ,
 ;
в частности,
;
в частности,
 ;
;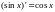 ;
; ;
;;
 ;
;;
;
;
.
Пример
1.
Найти
 ,
где
,
где
 .
.
Решение.
Находим первую производную
 .
Отсюда получим вторую производную
.
Отсюда получим вторую производную
 ,
а затем искомую третью производную
,
а затем искомую третью производную
 .
.
Ход
работы:
1)
 ,
,
 ;
2)
;
2)
 ,
;
3)
,
;
3)
 ,
,
 ;
4)
;
4)
 ,
;
5)
,
;
5)
 ,
,

Самостоятельная работа
I вариант |
II вариант |
1)
|
1)
|
2)
|
2)
|
3)
|
3)
|
4)
|
4)
|
5)
|
5)
|
Контрольные вопросы
Сформулируйте самостоятельно определение производной функции второго порядка.
Сформулируйте самостоятельно определение производной функции третьего порядка.
Сформулируйте самостоятельно определение производной функции n-го порядка.


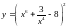


 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
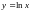 ,
,
 ,
,
 ,
,
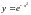 ,
,
 ,
,