1. Введение. 3
3.Определение кинематических характеристик кулисного механизма. 6
3.1.План положений механизма. 6
3.2.Планы аналогов скоростей. 6
4.Динамическая модель машинного агрегата. 8
5.Определение приведенного момента инерции звеньев кулисного механизма с переменным моментом инерции. 9
6.Определение приведённого момента сил сопротивления и движущих сил. 12
6.1.Определение приведенного момента сил сопротивления. 12
6.2.Определение работы сил сопротивления АС и движущих сил Ад. 13
6.3.Графическое интегрирование. 13
6.4.Определение приведенного момента движущих сил . 13
7.Определение постоянной составляющей приведенного момента инерции и установление необходимости в маховике. 15
8.Расчёт маховика. 16
Эскиз маховика 17
9. Динамический анализ машинного агрегата. 18
10.Динамический анализ кулисного механизма 19
10.1.Задачи и методы динамического анализа механизма 19
10.2.Кинематический анализ механизма 19
11.Силовой расчет механизма 22
11.1Определение сил инерции и моментов сил инерции звеньев 22
11.2.Кинетостатический силовой анализ механизма 22
12.Проектирование кулачкового механизма. 24
13.Кинематическое исследование планетарного зубчатого механизма. 28
13.1 Расчет параметров зацепления и зубчатых колес и построение картины эвольвентного зацепления. 29
Диаметры начальных окружностей: 30
30
30
30
Радиусы кривизны эвольвент на вершинах зубьев: 31
31
13.2 Оценка проектируемой передачи по качественным показателям 31
14. Подбор сечения для звеньев 32
Список литературы 37
Исследование
кулисного механизма
1. Введение.
На рисунке показана схема поперечно-строгального станка. Механизм состоит из кулисы 1, 3 и 5, ползунов 2 и 4. Строгание металла выполняется закрепленным в резцовой головке резцом.
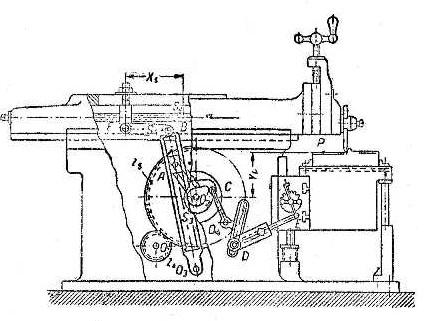
Рисунок 1
Длины
звеньев: a=0,22
м; b=0,14м;
LOA=0,1м;
=0,38
м;
Массы звеньев: m1= m3=11,4 кг; m2= 3,15; m4=3 кг; m5=34,2 кг;
Частота вращения кривошипа: n1=80 c-1;
Сила, приложенная к плите: F=30000 H;
Коэффициент
неравномерности вращения кривошипа:
;
Моменты инерции звеньев: IS4=0,0025 кг*м2; IS3=0,165 кг*м2; IS1=0,342кг*м2;
Момент инерции всех вращающихся деталей, приведенных к валу кривошипа: I0=0,03 кг*м2;
Максимальный
угол давления в кулачковом механизме:
=30о;
2
Целью структурного анализа механизма является определение формулы строения механизма и классификация входящих в его состав структурных групп, так как формула строения определяет порядок выполнения кинематического и силового расчетов, а классы структурных групп – методы расчетов.
Структурная
схема основного исполнительного
механизма изображена на рис.1. Число
подвижных звеньев n=5.
Число низших кинематических пар 
=7.
Число высших кинематических пар 
=0.
Число степеней свободы механизма:
W=3n-2 - =3∙5-2∙7-0=1
Рисунок 2
Так как механизм обладает 1 степенью подвижности, то одному из звеньев механизма относительно стойки придается определенное движение.
Определим класс механизма. Для этого расчленяем его на группы Ассура. Отделяем группы Ассура второго класса, образованные звеньями 2, 3 и 4,5. Остается ведущее звено 1 и стойка О, образующие механизм 1-ого класса.
Формула строения механизма : I(0,1) → II(2,3) → II(4,5).
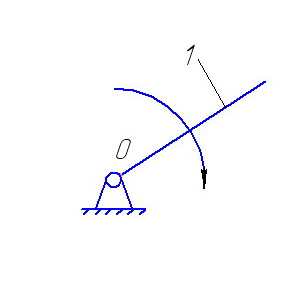
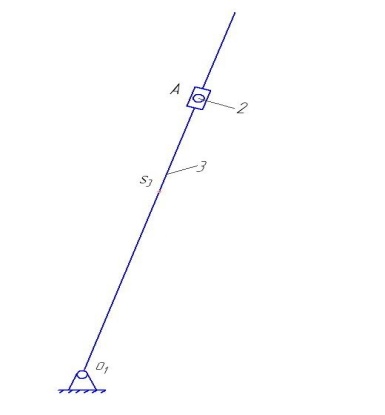
Механизм I класса Гр. Ассура (2,3)
II класса
2 Порядка
1 вида
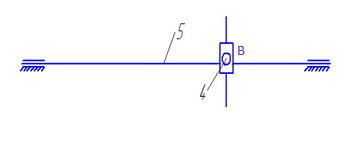
Гр. Ассура (4,5)
II класса
2 порядка
1 вида
Рисунок 3
Класс присоединенных групп – второй, поэтому рассматриваемый механизм относится ко второму классу.
3.Определение кинематических характеристик кулисного механизма.
3.1.План положений механизма.
Для построения планов положения механизма выберем масштабный коэффициент длины:
µs=0,00125 м/мм
Тогда
чертёжные отрезки, изображающие звенья
на чертеже, равны:
По полученным чертежным размерам строим 13 планов положений механизма.
Построение планов положений выполняется методом засечек, начиная с начального положения ползуна 2, через 300 по углу поворота кривошипа ОА.
3.2.Планы аналогов скоростей.
Требуется построить 13 планов аналогов скоростей и определить длины отрезков, изображающих аналоги скоростей на планах.
Для
построения аналога скорости точки
кривошипа А примем отрезок va=84
мм. Учитывая, что 
,
отложим vaOA
в направлении вращения звена OA.Построение
ведётся по группам Ассура в соответствии
с формулой строения механизма
I(0,1)→II(2,3) →
II(4,5).
Для построения аналогов скорости точки A воспользуемся векторными уравнениями:
Из
точки а плана аналогов проведем прямую
перпендикулярную звену
A
в данном положении, затем параллельную
A
из полюса v.
Точка пересечения этих прямых – точка
.
Отрезок
изображает аналог скорости
точки A.
Для построения отрезка vb, изображающего соответственно аналог скорость точки С воспользуемся теоремой подобия:
.
Для построения аналога скорости точки D воспользуемся векторными уравнениями:
Графически
решается так: из точки В проводим
вертикальную, а из полюса v
горизонтальную, на пересечении получаем
точку
.
Измеряем на планах аналогов скоростей длины соответствующих векторов и полученные значения заносим в табл. 1.
Таблица 1
№
|
Длины отрезков в мм |
||||||
va |
va' |
vb |
vd |
vs4 |
db |
vs3 |
|
1 |
84 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
84 |
49,00 |
127,00 |
115,00 |
119,00 |
47,00 |
63.50 |
3 |
84 |
84,00 |
266,00 |
268,00 |
267,00 |
11.00 |
134.00 |
4 |
84 |
58,00 |
159,00 |
150,00 |
152,50 |
53.00 |
79,50 |
5 |
84 |
8,58 |
17,50 |
17,30 |
16,90 |
8,09 |
8,75 |
5-6 |
84 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
84 |
31,9 |
51,20 |
49,80 |
49,30 |
21,80 |
25,60 |
7 |
84 |
60,00 |
81,40 |
77,10 |
78,20 |
25,90 |
40,70 |
8 |
84 |
77,57 |
95,90 |
92,06 |
94,00 |
16,97 |
47,95 |
9 |
84 |
83,9 |
99,75 |
104 |
103 |
1,55 |
49,90 |
10 |
84 |
79,6 |
96,99 |
98,20 |
97,30 |
14,3 |
48,495 |
11 |
84 |
64,2 |
85,30 |
82,30 |
83 |
25 |
42,65 |
12 |
84 |
37,5 |
58,40 |
48,10 |
52 |
24,3 |
29,2 |